Теоремы Больцан-Коши и Вейерштрасса

Доказательство следствия

Доказательство предела

Следствия

Доказательство предела

Доказательство следствия

Следствия

Доказательство следствий

Следствия

:

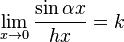
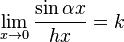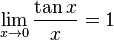
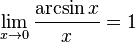
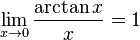
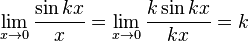
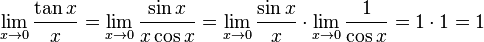
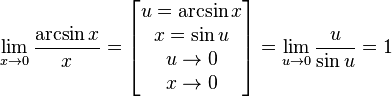
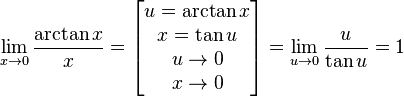
Замечательный показательно-степенной предел Править

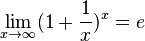(без доказательства)

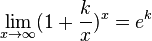
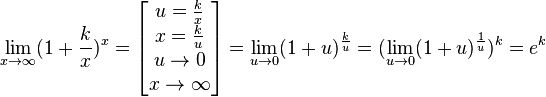
Замечательный логарифмический предел Править

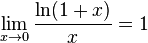
§ Используя замечательный показательно-степенной предел: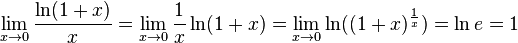

§ Используя правило Лопиталя: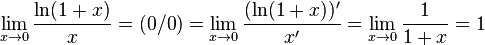

Замечательный показательный предел Править

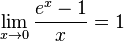
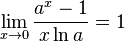для ,

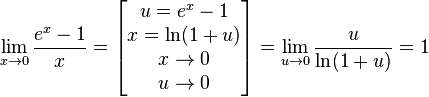
Замечательный степенной предел Править

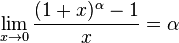(без доказательства)

Ответ: Т еорема Больцано — Вейерштрасса, или лемма Больцано — Вейерштрасса о предельной точке — предложение анализа, одна из формулировок которого гласит: из всякой ограниченной последовательности точек пространства R n можно выделить сходящуюся подпоследовательность. Теорема Больцано — Вейерштрасса, в особенности случай числовой последовательности (n =1), входит в каждый курс анализа. Она используется при доказательстве многих предложений анализа, например, теоремы о достижении непрерывной на отрезке функцией своих точных верхней и нижней граней. Теорема носит имена чешского математика Больцано и немецкого математика Вейерштрасса, которые независимо друг от друга её сформулировали и доказали.

Первая формулировка [править | править вики-текст]

Пусть предложена последовательность точек пространства R n:

x 1, x 2,…

и пусть эта последовательность ограничена, то есть

∥ xk ∥⩽ C, k =1,2,…

где C >0 — некоторое число.

Тогда из данной последовательности можно выделить подпоследовательность

xk 1, xk 2,…

которая сходится к некоторой точке пространства R n.

Теорему Больцано — Вейерштрасса в такой формулировке иногда называют принципом компактности ограниченной последовательности.

Расширенный вариант первой формулировки [править | править вики-текст]

Нередко теорему Больцано — Вейерштрасса дополняют следующим предложением.

Если последовательность точек пространства R n неограничена, то из неё можно выделить подпоследовательность, имеющую предел ∞.

Для случая n =1 эту формулировку можно уточнить: из любой неограниченной числовой последовательности можно выделить подпоследовательность, имеющую пределом бесконечность определенного знака (+∞ или −∞).

Таким образом, всякая числовая последовательность содержит подпоследовательность, имеющую предел в расширенном множестве действительных чисел R¯¯¯.

Вторая формулировка [править | править вики-текст]

Следующее предложение является альтернативной формулировкой теоремы Больцано — Вейерштрасса.

Всякое ограниченное бесконечное подмножество E пространства R n имеет по крайней мере одну предельную точку в R n.

Более подробно, это означает, что существует точка x 0∈R n, всякая окрестность Uε (x 0) которой содержит бесконечное число точек множества E.

Дата добавления: 2014-10-31