Лекция № 62. Тема 4 : Случайные величины и функции распределения

4.1. Случайные величины

Определение 1. Случайной величиной (СВ) называется величина Х, которая в результате опыта может принять то или иное значение, заранее неизвестно какое, т.е. 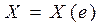, где е - элементарное событие.

СВ бывают двух типов:

1. Дискретные – если возможные значения СВ (значения, которые она принимает) могут быть перечислены. Например, число попаданий в мишень при п выстрелах, число вызовов на АТС и т.д.

2. Непрерывные – если возможные значения СВ непрерывно заполняют некоторый промежуток. Например, расстояние от точки попадания до центра мишени, время безотказной работы блока устройства.

Для того, чтобы задать СВ, необходимо знать её возможные значения и как часто она их принимает, т.е. с какой вероятностью. Для дискретных СВ закон распределения обычно задается в виде таблицы

X			…		…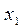
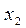
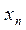
P			…		…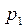

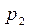
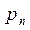
Замечание. Так как события 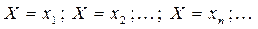образуют полную группу событий, то .

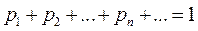Рассмотрим примеры наиболее распространённых дискретных СВ.

1. Биномиальное распределение.

X			…	k	…	n
p			…		…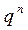

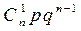
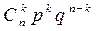
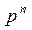
2. Распределение Пуассона.

X			…	n	…
p			…		…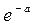

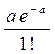
Пример 1. Монета брошена три раза. Построить закон распределения СВ – число появлений герба.

Здесь 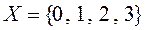. По формуле Бернулли вычислим соответст-вующие вероятности:

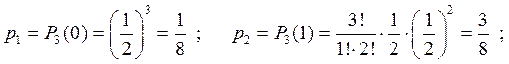
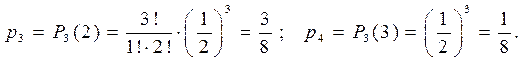
Проверим .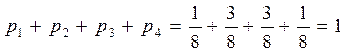

Получили закон распределения

X
p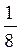

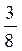
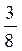
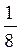
4.2. Функция распределения вероятностей для дискретной СВ

Для количественной характеристики распределения вероятностей удобно пользоваться не вероятностью события 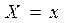, а вероятностью события .

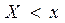Определение 2. Функция 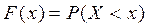называется функцией распределения вероятностей случайной величины Х или интегральной функцией распределения.

Геометрически это означает, что 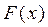- вероятность того, что СВ примет значение, лежащее левее х.

Пример 2. Построить функцию 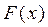распределения вероятностей для примера 1.

1. 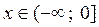, для таких значений .

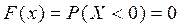2. 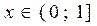, для таких значений .

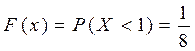3. 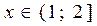, для таких значений .

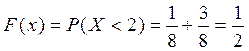4. , для таких значений .

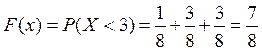5. 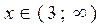, для таких значений .

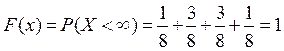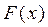
0,5

0 1 2 3 4 х

Из определения функции распределения следуют её свойства:

1.

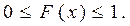
2. 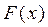- неубывающая функция.

3. .

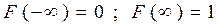4. Вероятность того, что СВ примет значение, заключенное в интер-вале 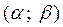, равно .

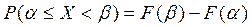Рассмотрим события 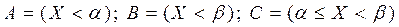, тогда 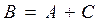. Так как А и С несовместные события, то 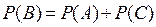. Тогда учитывая, что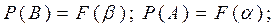 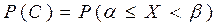, получим .

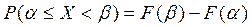5. 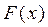имеет разрывы первого рода во всех точках, соответству-ющих возможным значениям СВ, а величина скачка равна

.

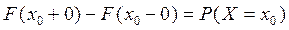4.3. Непрерывная СВ. Функция распределения

и плотность распределения вероятностей

Функция распределения вероятностей непрерывной СВ определяется аналогично как и для дискретной 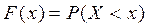. В этом случае 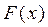является непрерывной функцией и обладает свойствами 1-4. Однако, если 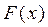непрерывная, то вероятность любого определённого значения непрерывной СВ равна нулю, так как

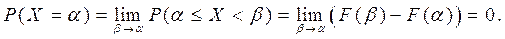
Для локальной характеристики непрерывной СВ вводится понятие плотности распределения вероятностей.

Пусть имеется непрерывная случайная величина Х с функцией распре-деления 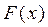. Вычислим вероятность попадания этой СВ в интервал 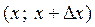. По свойству 4, получаем .

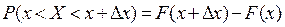Рассмотрим отношение 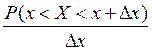, т.е. “среднюю“ вероятность и устремим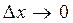

.

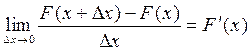Определение 3. Плотностью распределения вероятностей или диффе-ренциальной функцией распределения называется функция .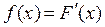

Из этого определения следуют её свойства:

1. 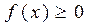, как производная от неубывающей функции.

2. Вероятность попадания СВ в интервал 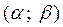равна

так как 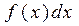- вероятность попадания СВ в интервал длины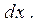

3. 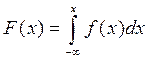, так как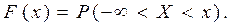

4. 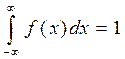, что следует из свойства 3 и того, что

Пример 3. Найти интегральную функцию по заданной дифференциаль-ной и вероятность попадания СВ в интервал 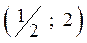, если

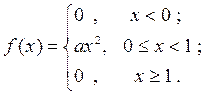
Найдём значение параметра а из свойства 4 дифференциальной функции

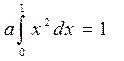или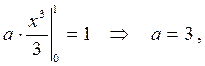

а по свойству 3 находим интегральную функцию

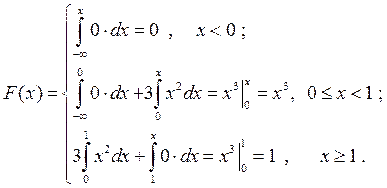
Вероятность попадания в заданный интервал можно определить по формулам из свойства 4 интегральной функции или из свойства 2 дифференциальной функции. Воспользуемся формулой

.

Приведём графики дифференциальной и интегральной функций.

3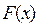

0 1 х 0 1 х

Дата добавления: 2014-11-16