Статистические методы оценки измерений в экспериментальных исследованиях

Здесь мы продолжим начатое в подразделах 7.1, 7.3 и 7.4 рассмотрение статистических методов обработки экспериментальных данных.

Как уже неоднократно отмечалось выше, измерения являются основной составной любого эксперимента. От тщательности измерений и последующих вычислений зависят результаты эксперимента. Поэтому каждый экспериментатор должен знать закономерности измерительных процессов:

Ø уметь правильно измерить изучаемые величины;

Ø оценить погрешности при измерениях;

Ø правильно, с требуемой точностью вычислить значения величин и их минимальное количество;

Ø определить наилучшие условия измерений, при которых ошибки будут наименьшими, и произвести общий анализ результатов измерений.

Что такое измерение, какими бывают измерения, что такое точность измерения, классификация погрешностей, среднее значение, эмпирическая дисперсия и СКО и др., мы рассмотрели в разделе 7. Поскольку в радиотехнике и в телекоммуникации важное место занимает борьба со случайными погрешностями (шумами, помехами естественного и искусственного происхождения), мы в данном разделе основное внимание уделим именно им.

8.3.1. Некоторые сведения о нормальном законе распределения случайной величины

Процедура статистического анализа экспериментальных данных основывается на предположении о том, что эти данные являются случайной величиной, распределенной по нормальному закону.

Случайная будет распределена по нормальному закону, если она «представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало» (теорема Ляпунова [15]).

При экспериментальном исследовании какого-либо процесса измеряемый результат последнего является случайной величиной, на которую оказывает влияние огромное число факторов. Именно поэтому результат исследования, как правило, является случайной величиной, распределенной по нормальному закону.

При достаточно большом числе повторностей нормальный закон распределения проявляется в том, что:

 абсолютные отклонения одинаковой величины, но разного знака встречаются одинаково часто;

‚ большие по модулю абсолютные отклонения встречаются реже, чем меньшие, т. е. вероятность появления той или иной погрешности уменьшается с увеличением модуля этой погрешности.

Чем меньше величина абсолютного отклонения, тем больше точность измерения. Однако при одной и той же погрешности точность измерения может быть различной. Например, результат измерения, записанный в виде 45.0±0.2, будет

иметь большую точность, чем результат 0.54 ±0.2. Чтобы иметь возможность сравнивать точность различных измерений, рассчитывают относительную погрешность измерения, выражая ее в процентах

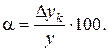(8.1)

За оценку истинного значения случайной величины 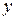обычно принимают среднее арифметическое из всех повторностей:

(8.2)

Для всех повторностей можно записать

(8.3)

або

(8.4)

Вправа 8.1

Доведіть, що формули (8.3) і (8.4) є коректними.

Если случайная величина является распределенной по нормальному закону, то при достаточно большом числе повторностей будет справедливым равенство

(8.5)

Вправа 8.2

З якої властивості нормального розподілу випливає рівність (8.5)?

Следовательно: только при среднеарифметическое 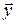равно истинному значению .

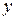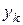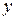Как уже отмечалось, более часто будут встречаться меньшие по модулю абсолютные отклонения, т. е. их появление будет более вероятно. Обозначим вероятность появления в интервале от до через , а вероятность появления результата в интервале от до 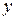– через . Если , то для приращения вероятности будет справедливым равенство

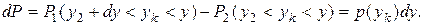
Тогда 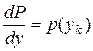будет тем больше, чем меньше абсолютное отклонение.

Величина 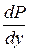называется плотностью распределения случаиной величины и обозначается :

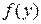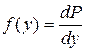. (8.6)

При известной функции плотности распределения 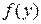вероятность попадания 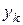в интервал можно рассчитать по формуле

(8.7)

Если расширить интервал до 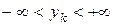, то вероятность будет равна

Последнее соотношение показывает, что 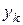обязательно примет одно из значений, лежащих в интервале от до . Плотность нормального распределения случайной величины 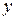(рис. 8.1), во-первых, симметрична относительно 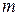(математического ожидания случайной величины 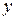), во-вторых, достигает максимального значения при и, в третьих, быстро стремится к нулю при увеличении 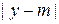Функция плотности нормального распределения случайной величины задается двумя параметрами: истинным значением 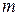и СКО :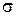

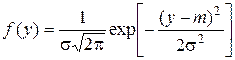. (8.8)

Квадрат СКО, как известно, называется дисперсией случайной величины и является количественной характеристикой разброса результатов вокруг истинного значения .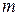

На рис. 8.2 изображены графики плотности нормального распределения при различных значениях дисперсии, причем . Очевидно, кривая 1характеризует плотность распределения случайной величины, воспроизводимость которой в повторных измерениях лучше, чем воспроизводимость случайных величин, имеющих плотность распределения 2 и 3.

Если ввести переменную 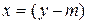и за единицу измерения по оси абсцисс принять вычисленный' параметр 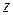при 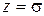, то так называемая нормированная плотность нормального распределения будет иметь вид

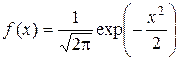. (8.9)

Кривая плотности распределения в этом случае будет симметричной относительно ее вид не будет зависеть от величины дисперсии.

Подробнее о нормированной плотности нормального распределения, о том, как можно путем замены переменных осуществляется переход от плотности (8.8) к плотности (8.9) и, наконец, как с помощью такого перехода можно существенно уменьшить объем таблицы для расчета оценок интеграла (8.7), см. приложении Б, комментарий к табл. Б1. Кроме того, ниже мы рассмотрим пример того, как пользоваться табл. Б1.

8.3.2. Экспериментальные оценки истинных значений измеряемой случайной величины и ее СКО

Если в распоряжении исследователя находится конечное число независимых результатов повторностей одного и того же опыта, то он может получить лишь экспериментальные оценки истинного значения и дисперсии результата опыта.

Следует стремиться к тому, чтобы оценки обладали следующими свойствами:

 несмещенностью, проявляющейся в том, что теоретическое среднее из генеральной совокупности результатов совпадает с истинным значением измеряемого параметра;

‚ состоятельностью, когда оценки при неограниченном увеличении числа измерений могут иметь сколь угодно малый доверительный интервал при доверительной вероятности, стремящейся к единице;

ƒ эффективностью, проявляющейся в том, что из всех несмещенных оценок данная оценка будет иметь наименьшие рассеяния (наименьшую дисперсию).

Среднеарифметическое значение 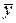, если измеренное в 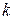-том опыте значение 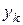является случайной величиной, распределенной по нормальному закону, будет несмещенной, состоятельной и эффективной оценкой истинного значения .

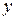Экспериментальная оценку СКО будем, как и выше, обозначать буквой с указанием в скобках символа анализируемой величины. Например, – СКО единичного результата; 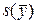– СКО среднего результата (стандартная ошибка).

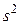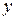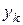Квадрат экспериментальной оценки СКО является экспериментальной оценкой дисперсии. Если истинное значение известно, то по повторностям находят эффективную, состоятельную и несмещенную оценку дисперсии по формуле

(8.10)

Если по результатам рассчитывают оценку истинной значения 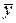по формуле (8.2), а затем, используя те же результаты, рассчитывают абсолютные отклонения, то оценку дисперсии единичного результата находят по выражению

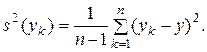(8.11)

Разность между числом независимых результатов в повторностях и числом уравнений, в которых эти результат использованы для расчета неизвестных оценок (в рассматриваемом случае полученные результаты использовались лишь одном уравнении – для расчета 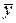), называют числом степеней свободы 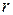. В данном случае 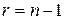. Подробнее о числе степеней см. ниже.

Так как средняя оценка 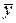является более точной, чем единичная 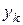, то и дисперсия (разброс) средних будет меньше дисперсии единичных результатов.

В статистике доказывается, что оценка дисперсии среднего результата будет меньше оценки дисперсии единичного в раз, если 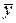рассчитано по всем единичным результатам 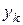повторностей:

(8.12)

8.3.3. Доверительный интервал оценок СКО

Для получения возможно более точной оценки дисперсии нужно провести опыт с возможно большим числом повторностей. При конечном числе степеней свободы полученная оценка дисперсии является смещенной и доверительный интервал опенки не будет симметричен относительно этой оценки

(8.13)

где 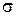– истинное значение СКО; и – коэффициенты, значения которых можно взять из соответствующей таблицы (Додаток Б, Таблиці розподілів, таблиця Б.5) в зависимости от принятого уровня значимости 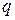и числа степеней свободы 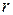при определении оценки дисперсии ; .

Приклад 8.1

Пусть проведены измерения некоторого параметра, например, сигнала. Всего измерений (повторностей) было . По этой выборке случайных величин 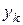получена оценка СКО . Требуется найти доверительный интервал этой оценки с доверительной вероятностью .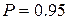

Розв‘язання.

Найдем число степеней свободы: . По таблице Б.5 Находим для : , откуда . .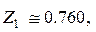

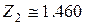Далее: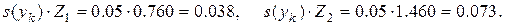

Окончательно имеем:

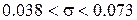, то есть, с вероятностью 0.95 истинное значение СКО лежит в интервале .

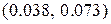É

Вправа 8.3

Найдите доверительный интервал СКО при условии, что исходные данные те же, что и в примере 8.1, но .

Вправа 8.4

Найдите доверительный интервал СКО при условии, что исходные данные те же, что и в примере 8.1, но число степеней свободы увеличено до 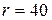, то есть практически в 2 раза увеличен объем выборки.

Вправа 8.5

Сравните результаты решения примера 8.1 и упражнений 8.3, 8.4 и сделайте выводы о том:

 как изменение доверительной вероятности (уровня значимости) при прочих равных условиях влияет на ширину доверительного интервала;

‚ как на величину доверительного интервала влияет объем выборки при прочих равных условиях.

8.3.4. Выявление грубых ошибок (промахов) в результатах измерений

Среди повторностей опыта могут быть результаты, значительно отличающиеся от других результатов этой же серии. Это может быть связано либо с какой-то грубой ошибкой при проведении данной повторности опыта (измерения), либо с неизбежным влиянием случайных причин.

Грубую ошибку можно определить по критерию максимального отклонения 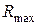, взятого из таблицы Б.6 (приложение Б, Таблицы распределений). Для этого 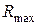сравнивают с величиной 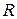, равной

(8.14)

Если , то данный результат должен исключаться из дальнейшего анализа. При этом оценка 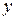должна быть пересчитана, изменятся абсолютные отклонения и соответственно оценки дисперсии и . Возможен случай, когда исключаются сразу несколько ошибочных результатов.

Приклад 8.2

Пусть имеется 20 измерений.

Результаты измерений 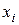записаны в табл. 8.1 и приведены на графике рис. 8.3. Необходимо их проанализировать. Анализ средств и результатов измерений показал, что систематических ошибок в эксперименте не обнаружено.

Выясним, не содержат ли измерения грубых ошибок с уровнем значимости не больше 0.05.

Розв‘язання.

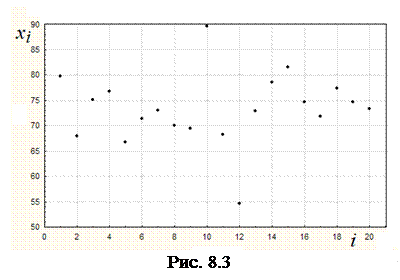
Первичный, визуальный анализ данных табл. 8.1 и графика рис. 8.3 показывает, что по крайней мере 2 результата измерени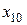й ( и 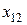) существенно отличаются от других данных статистического ряда. Являются ли эти результаты следствием промахов мы и должны выяснить. Воспользуемся критерием максимального отклонения.

Найдем оценки среднего значение и СКО 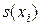. Получим: 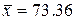и .

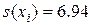Вправа 8.6

Знайдіть за даними табл.. 8.1 оцінки середнього значення , дисперсії та СКО випадкової величини .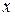

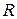Находим , , вычисляем величину . Оценки этих статистик приведены в соответствующих столбцах таблицы. Находим по таблице Б.5 для и уровня значимости 0.05 . В нашем случае условие 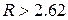выполняется только для одного результата, а именно, для 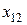. То есть 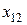необходимо исключить из дальнейшего анализа, поскольку этот результат с вероятностью не менее 0.95 является грубой ошибкой – промахом.

É

Поскольку мы обнаружили в данных примера 8.2 грубую ошибку, ее нужно исключить. Кроме того, в данных присутствует еще одна подозрительная величина .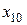

Дата добавления: 2014-11-18