Приклад 8.6

В примере 8.5 мы путем соответствующей обработки экспериментальных данных получили статистический ряд 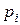(см. табл. 8.5) и построили соответствующую ему гистограмму (рис. 8.4). Из визуального анализа гистограммы можно сделать вывод, что случайная величина Х вполне вероятно подчиняется нормальному распределению. Чтобы проверить эту гипотезу, необходимо провести выравнивание статистического ряда с помощью нормального закона (8.15).

Розв‘язання.

Нормальный закон зависит от двух параметров: 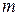и 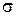. Подберем эти параметры так, чтобы сохранить первые два момента – математическое ожидание и дисперсию – статистического распределения.

Середнє арифметичне за групованою вибіркою (статистичним рядом, гістограмою) обчислюється за формулою 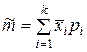, де 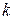–число інтервалів (у нашому випадку 10), –середина і -того інтервалу.

Для задачі, що розглядається, отримаємо:

Визначимо тепер дисперсію за групованою вибіркою. У загальному випадку, коли оцінка математичного очікування за модулем суттєво відрізняється від нуля, дисперсію треба розраховувати безпосередньо за виразом

.

У випадку, коли , можна скористатися наближеним методом. Для цього спочатку знаходять початковий момент другого порядку

.

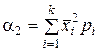Тепер наближену оцінку дисперсії можна знайти за відомою формулою теорії ймовірності, яка з нашими позначеннями має вигляд

У нашому випадку 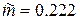, тобто його величину не можна назвати дуже малою. Скористаємося загальною формулою. У нашому випадку вона має вигляд:

.

Підставимо до неї дані з таблиці 8.5 і отримаємо6

Таким чином,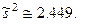

Скористаємося тепер теоретичним нормальним законом розподілу з параметрами: , тобто,

.

На рис. 8.5 наведено графік цієї функції разом з тією гістограмою, яку наведено на рис. 8.4.

Аналізуючи графіки, які наведено на рис. 8.5, можна зробити висновок, що візуально гістограма і теоретична густина ймовірності нормального розподілу досить добре узгоджуються одна з одною, але є інтервали, де має місце досить суттєве розузгодження. На практиці майже завжди необхідно отримати деякі кількісні оцінки такого узгодження, чи не виникло воно випадково, яка ймовірність такої події. У наступному прикладі ми отримаємо такі оцінки

É

8.4.4. Критерии согласия

Рассмотрим один из вопросов, связанных с проверкой правдоподобия гипотез, а именно – вопрос о согласованности теоретического и статистического распределения.

Пусть данное статистическое распределение выровнено с помощью некоторой теоретической кривой 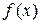(рис. 8.5). Как бы хорошо ни была подобрана теоретическая кривая, между нею и статистическим распределением неизбежны некоторые расхождения. Естественно возникает вопрос: объясняются ли эти расхождения только случайными обстоятельствами, связанными с ограниченным числом наблюдений, или они являются существенными и связаны е тем, что подобранная нами кривая плохо выравнивает данное статистическое распределение. Для ответа на такой вопрос служат так называемые «критерии согласия».

Идея применения критериев согласия заключается в следующем. На основании данного статистического материала нам предстоит проверить гипотезу 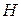, состоящую в том, что случайная величина X подчиняется некоторому определенному закону распределения. Этот закон может быть задан в той или иной форме: например, в виде функции распределения .

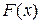Для того чтобы принять или опровергнуть гипотезу 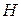, рассмотрим некоторую величину 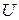, характеризующую степень расхождения теоретического и статистического распределений. Величина 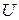может быть выбрана различными способами; например, в качестве 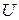можно взять сумму квадратов отклонений теоретических вероятностей 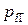от соответствующих частот 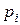или же сумму тех же квадратов с некоторыми коэффициентами («весами»), или же максимальное отклонение статистической функции распределения 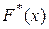от теоретической 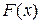и т. д. Допустим, что величина 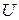выбрана тем или иным способом. Очевидно, это есть некоторая случайная величина. Закон распределения этой случайной величины зависит от закона распределения случайной величины X,над которой производились опыты, и от числа опытов . 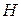Если гипотеза верна, то закон распределения величины 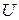определяется законом распределения величины X (функцией 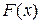и числом .

Допустим, что этот закон распределения нам известен. В результате данной серии опытов обнаружено, что выбранная нами мера расхождения 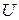приняла некоторое значение . Спрашивается, можно ли объяснить это случайными причинами или же это расхождение слишком велико и указывает на наличие существенной разницы между теоретическим и статистическим распределениями и, следовательно, на непригодность гипотезы 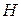? Для ответа на этот вопрос предположим, что гипотеза 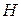верна, и вычислим вероятность того, что за счет случайных причин, связанных с недостаточным объемом опытного материала, мера расхождения 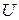окажется не меньше, чем наблюденное нами в опыте значение , т. е. вычислим вероятность события. . Если эта вероятность мала, то гипотезу 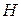следует отвергнуть как мало правдоподобную; если же эта вероятность значительна, следует признать, что экспериментальные данные не противоречат гипотезе .

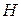Возникает вопрос о том, каким же способом следует выбирать меру расхождения 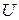?Оказывается, что при некоторых способах ее выбора закон распределения величины 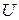обладает весьма простыми свойствами и при достаточно большом практически не зависит от функции 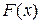. Именно такими мерами расхождения и пользуются в математической статистике в качестве критериев согласия.

Рассмотрим один из наиболее часто применяемых критериев согласия – так называемый «критерий 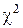» Пирсона. Применение критерия 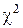рассмотрим на примере.

Перевіримо гіпотезу 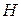про те, що випадкова величина 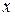, статистичний ряд для якої наведено у таблицці 8.5, э такою, яка підпорядковується нормальному розподілу.

Дата добавления: 2014-11-18