
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Бесконечно малые последовательности и их свойства
I Два определения
Определение 1 (язык «e-N»). Последовательность  называют бесконечно малой (б.м.), если для любого (сколь угодно малого) положительного числа e найдется номер N=N (e) (зависящий, вообще говоря, от e) начиная с которого выполняется неравенство
называют бесконечно малой (б.м.), если для любого (сколь угодно малого) положительного числа e найдется номер N=N (e) (зависящий, вообще говоря, от e) начиная с которого выполняется неравенство 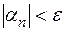 .
.
Используя квантор всеобщности " и квантор существования $, это определение можно записать следующим образом:
 .
.
Для дальнейшего нам понадобится одно важное понятие. Вот его определение:
интервал вида  называется e -окрестностью точки
называется e -окрестностью точки 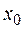 .
.
Неравенство 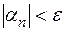 , фигурирующее в определении 1, равносильно двойному неравенству
, фигурирующее в определении 1, равносильно двойному неравенству 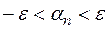 , что означает следующее:
, что означает следующее: 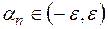 . Теперь можем дать второе определение (равносильное первому).
. Теперь можем дать второе определение (равносильное первому).
Определение 2 (язык «окрестностей»). Последовательность  называется б.м., если любая (сколь угодно малая) e -окрестность нуля содержит все члены последовательности, начиная с некоторого номера N (e) (зависящего, вообще говоря, от e).
называется б.м., если любая (сколь угодно малая) e -окрестность нуля содержит все члены последовательности, начиная с некоторого номера N (e) (зависящего, вообще говоря, от e).
Из определения 2 можно сделать вывод: вне любой (сколь угодно малой) e -окрестности нуля содержится лишь конечное число членов б.м. последовательности.
Для б.м. последовательности  принято обозначение
принято обозначение  (читается «о малое от 1»), иногда уточняют, добавляя: n® ¥.
(читается «о малое от 1»), иногда уточняют, добавляя: n® ¥.
II Две эталонные б.м.
1)  при a > 0. Примеры:
при a > 0. Примеры:  .
.
2)  при
при  . Примеры:
. Примеры: 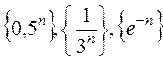 .
.
Доказательство первого утверждения
Возьмем и зафиксируем число 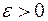 . Надо найти номер
. Надо найти номер 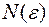 , начиная с которого
, начиная с которого
 .
.
В качестве номера 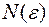 можно взять
можно взять  , ибо если
, ибо если  т.е.
т.е. 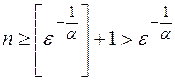 и получаем
и получаем 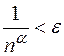 . Так как такой номер можно найти
. Так как такой номер можно найти  , то тем самым доказана бесконечная малость последовательности
, то тем самым доказана бесконечная малость последовательности 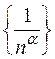 .
.
Второе утверждение доказывается аналогично, только для решения показа-тельного неравенства используются логарифмы.
III Основные свойства
Эти свойства нужны для того, чтобы доказывать бесконечную малость последовательности, не применяя определения (1 или 2).
1) Пусть  . Тогда:
. Тогда:
а) 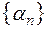 – ограничена;
– ограничена;
б)  ;
;
в)  ;
;
г)  ;
;
д) если 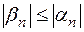 или
или  , то
, то  .
.
2) Произведение ограниченной последовательности на бесконечно малую есть бесконечно малая.
3) Сумма, разность и произведение б.м. есть б.м.
Для доказательства 1а) возьмем конкретное e, например, e = 1. Тогда  . Вне интервала (-1,1) могут находиться лишь конечное число членов, т.е.
. Вне интервала (-1,1) могут находиться лишь конечное число членов, т.е.  . Т.к. в конечном множестве чисел есть наибольшее и наименьшее, то все члены
. Т.к. в конечном множестве чисел есть наибольшее и наименьшее, то все члены  находятся между
находятся между  и
и 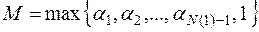 , т.е.
, т.е. 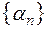 - ограничена.
- ограничена.
Докажем свойство 2. Пусть  , а
, а 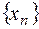 - ограничена, т.е.
- ограничена, т.е.  . Для доказательства того, что
. Для доказательства того, что  необходимо взять произвольное
необходимо взять произвольное 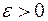 и найти номер, начиная с которого
и найти номер, начиная с которого  . Итак, пусть
. Итак, пусть 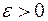 - произвольное, рассмотрим число
- произвольное, рассмотрим число  . Т.к.
. Т.к.  , то для этого
, то для этого  . Тогда имеем:
. Тогда имеем:
 ,
,
т.е., начиная с  имеем
имеем  , следовательно
, следовательно 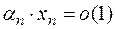 .
.
Примеры использования.
а)  , т.к.
, т.к. 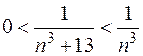 , а
, а  - эталонная б.м.
- эталонная б.м.
б)  , т.к.
, т.к.  и
и 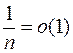 , а
, а  - ограниченная.
- ограниченная.
в) Т.к.  для
для  , то
, то  . Следовательно
. Следовательно 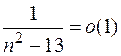 .
.
Замечание. Частное двух б.м. может быть каким угодно.
Задачи (для самостоятельного решения).
1. Пусть 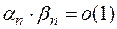 . Следует ли отсюда, что
. Следует ли отсюда, что  или
или  ?
?
2. Может ли среди членов б.м. последовательности быть бесконечно много
одинаковых членов? Если да, то каких?
Лекция 3
|
|
Дата добавления: 2014-11-08; Просмотров: 1252; Нарушение авторских прав?; Мы поможем в написании вашей работы!