Диференціальні рівняння з відокремлюваними змінними

Рівняння виду , (6)

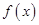де і 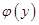– задані і неперервні на деякому інтервалі функції називається диференціальним рівнянням з відокремлюваними змінними.

Права частина рівняння (6) являє собою добуток двох множників, кожен з яких є функцією лише однієї змінної. Щоб розв’язати рівняння (6), треба відокремити змінні. Для цього замінимо 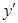на 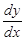, поділимо обидві частини рівняння (6) на 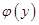(вважатимемо, що 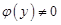) і помножимо на 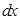, тоді рівняння (6) запишеться у вигляді

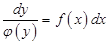. (7)

Диференціальне рівняння виду (7), в якому множник при 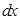є функцією, яка залежить лише від 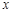, а множник при 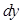є функцією, яка залежить лише від 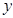, називається диференціальним рівнянням з відокремленими змінними.

Оскільки рівняння (7) містить тотожно рівні диференціали, то відповідні невизначені інтеграли відрізняються між собою на сталу величину, тобто

.

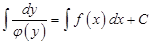Диференціальне рівняння (7) є окремим випадком рівняння виду

.

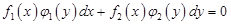Приклад 1.2. Знайти загальний розв’язок рівняння 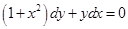. Знайти його частинний розв’язок при заданих початкових умовах: .

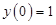●Розділимо обидві частини рівняння на (1+x²)y≠0.

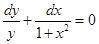
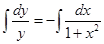
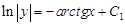
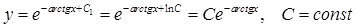
Це загальний розв’язок рівняння. Знайдемо його частинний розв’язок:

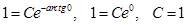
Отже, 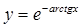- частинний розв’язок рівняння. ●

Розглянемо рівняння 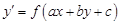(8), де 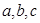- задані числа.

Заміною 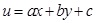рівняння (8) зводиться до рівняння з відокремлюваними змінними.

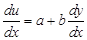
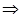
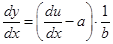
Підставимо у рівняння (8):

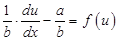
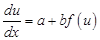
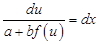
Інтегруючи це рівняння і замінюючи 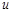на 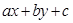, дістанемо загальний інтеграл рівняння (8).

Приклад 1.3. Розв’язати рівняння .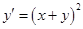

● Покладемо 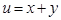, тоді 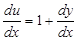або 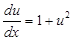. Звідки 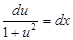. Інтегруючи це рівняння, знаходимо 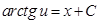, тобто 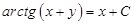- загальний розв’язок рівняння. ●

► ПИТАННЯ ДЛЯ САМОПЕРЕВІРКИ

1. Що називається диференціальним рівнянням першого порядку?

2. Які диференціальні рівняння першого порядку називаються неявним ДР?

3. Запишіть диференціальні рівняння першого порядку в диференціальній формі.

4. Що називається розв’язком диференціального рівняння першого порядку?

5. Сформулюйте теорему про існування і єдиність розв’язку диференціального рівняння першого порядку (теорема Коші).

6. Що називається частинним розв’язком диференціального рівняння першого порядку?

7. Що називається рівнянням з відокремлюваними змінними?

8. Алгоритм розв’язку диференціального рівняння з відокремлюваними змінними.

Дата добавления: 2014-12-17