
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Визначник та його властивості
|
|
|
|
Тема: Перестановки. Підстановки.
ПРАКТИЧНЕ ЗАНЯТТЯ № 2
Задачі для самостійного розв’язування
1. Для заданих матриць виконайте зазначені дії:
а) для матриць 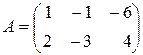 ,
, 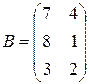 ,
,  обчисліть
обчисліть 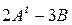 ,
, 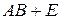 ,
,  ,
, 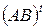 ,
,  ,
,  ,
,  ,
, 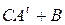 ;
;
б) для матриць 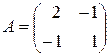 ,
, 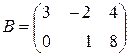 ,
, 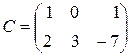 обчисліть
обчисліть 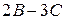 ,
, 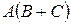 ,
,  ,
,  ,
,  ;
;
в) для матриць  ,
, 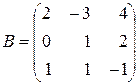 ,
, 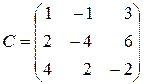 обчисліть
обчисліть 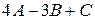 ,
, 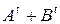 ,
,  ,
,  .
.
2. Знайдіть добутки матриць:
а)  ; б)
; б) 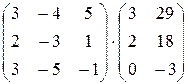 ; в)
; в)  ;
;
г) 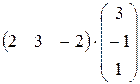 ; д)
; д) 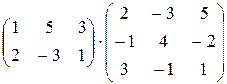 ; е)
; е)  ;
;
ж)  ; з)
; з)  ; і)
; і) 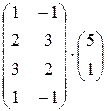 .
.
3. Обчисліть значення многочлена 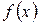 від матриці
від матриці 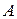 :
:
а)  ,
, 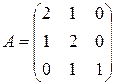 ; б)
; б) 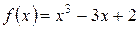 ,
, 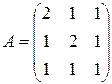 .
.
Зауваження 4. При знаходженні значення многочлена 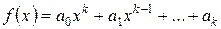 від матриці
від матриці 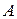 будемо вважати його вільний член
будемо вважати його вільний член  рівним
рівним 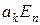 , де
, де  – порядок матриці
– порядок матриці 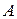 .
.
4. Розв’яжіть системи матричних рівнянь:
а) 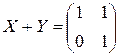 ,
, 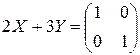 ,
,
б) 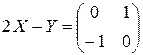 ,
, 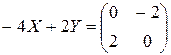 .
.
Перестановкою  натуральних чисел
натуральних чисел 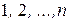 називається довільний впорядкований набір цих чисел.
називається довільний впорядкований набір цих чисел.
Приклад. Перестановками чисел 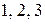 є
є 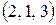 ,
,  ,
, 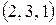 .
.
Теорема. Існує 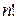 різних перестановок з
різних перестановок з  елементів.
елементів.
Інверсією в перестановці називається пара елементів  таких, що
таких, що  та
та 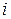 перебуває лівіше
перебуває лівіше 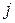 . Кількість інверсій у перестановці
. Кількість інверсій у перестановці  позначається
позначається 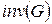 .
.
Приклад. а) У перестановці 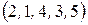 число 2 утворює інверсію
число 2 утворює інверсію  , 1 не утворює інверсій, 4 –
, 1 не утворює інверсій, 4 –  , 3 та 5 – не утворюють. Отже,
, 3 та 5 – не утворюють. Отже, 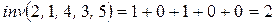 .
.
б) Наведемо всі інверсії перестановки 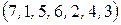 :
: 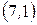 ,
, 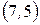 ,
, 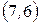 ,
, 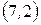 ,
, 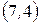 ,
, 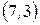 ;
;  ,
, 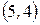 ,
,  ;
; 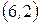 ,
, 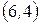 ,
, 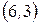 ;
;  . Підрахуємо їх кількість:
. Підрахуємо їх кількість: 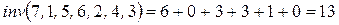 .
.
Перестановка називається парною, якщо в ній число інверсій парне, непарною – у противному випадку (див. попередній приклад).
Транспозицією називається таке перетворення перестановки, при якому міняються місцями два елементи перестановки (не обов’язково ті, що стоять поруч), а всі інші залишаються на місці. Всі 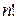 перестановок з
перестановок з  чисел
чисел 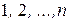 можна розташувати в такому порядку, що кожна наступна буде отримуватись з попередньої однією транспозицією, причому починати можна з будь-якої перестановки.
можна розташувати в такому порядку, що кожна наступна буде отримуватись з попередньої однією транспозицією, причому починати можна з будь-якої перестановки.
Теорема. Будь-яка транспозиція змінює парність перестановки.
Підстановкою  -го порядку (степеня)називають взаємно однозначне відображення множини
-го порядку (степеня)називають взаємно однозначне відображення множини 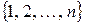 у себе. Зазвичай підстановки записують у вигляді матриці розміру
у себе. Зазвичай підстановки записують у вигляді матриці розміру 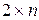 . У першому рядку розміщуються елементи від 1 до
. У першому рядку розміщуються елементи від 1 до  (прообрази), а в другому рядку – елементи, в які вони відображаються (образи).
(прообрази), а в другому рядку – елементи, в які вони відображаються (образи).
|
|
|
Приклад. Підстановка четвертого порядку  .
.
Підстановка – це дві перестановки, записані одна під іншою у вигляді матриці. Підстановка називається парною (непарною) якщо сума інверсій в обох рядках є числом парним (непарним).
Приклад. 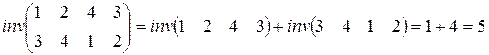 , отже підстановка непарна.
, отже підстановка непарна.
Зауваження. Якщо в підстановці поміняти місцями стовпці, то одержимо іншу форму запису тієї ж підстановки.
Приклад.  .
.
Парність підстановки не залежить від форми її запису.
Приклад.  ,
, 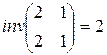 .
.
Визначником (детермінантом) квадратної матриці 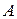 порядку
порядку  називається число
називається число  (або
(або  , або
, або 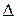 ), що дорівнює сумі
), що дорівнює сумі 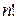 доданків, кожний з яких є добутком
доданків, кожний з яких є добутком  елементів цієї матриці, взятих по одному з кожного рядка та кожного стовпця зі знаком «плюс», якщо підстановка, складена з індексів елементів цього добутку, парна та зі знаком «мінус», якщо непарна.
елементів цієї матриці, взятих по одному з кожного рядка та кожного стовпця зі знаком «плюс», якщо підстановка, складена з індексів елементів цього добутку, парна та зі знаком «мінус», якщо непарна.
Позначення: при
 ,
,  ,
,  ;
;
 ,
, 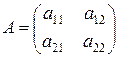 ,
, 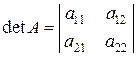 ;
;
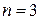 ,
,  ,
, 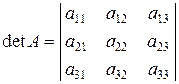 ;
;
…
 ,
, 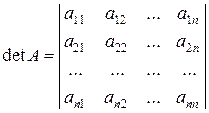 .
.
Означення детермінанта матриці порядку  , з якого випливає правило його обчислення, є досить складним для сприйняття й застосування. Однак відомі методи, що дозволяють обчислити визначники високих порядків на основі визначників нижчих порядків.
, з якого випливає правило його обчислення, є досить складним для сприйняття й застосування. Однак відомі методи, що дозволяють обчислити визначники високих порядків на основі визначників нижчих порядків.
Обчислення визначника 2-го порядку ілюструється схемою:

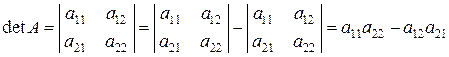 .
.
Приклад.
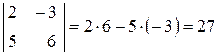 .
.
При обчисленні визначника 3-го порядку зручно користуватися:
- правилом трикутників, яке ілюструється схемою:


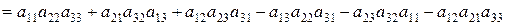 .
.
- правилом прямих (правилом Саррюса), яке ілюструється схемою:
 |
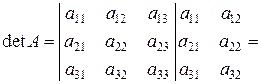
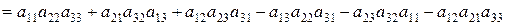 .
.
|
|
|
|
|
Дата добавления: 2014-12-17; Просмотров: 693; Нарушение авторских прав?; Мы поможем в написании вашей работы!