Теорема Умова – Пойнтинга

Физическое состояние любой системы наиболее отчётливо проявляется при выяснении происходящих в ней энергетических процессов. В этом отношении важное значение имеет теорема об энергии электромагнитного поля, сформулированная Пойнтингом (интеграл энергии уравнений Максвелла).

Идеи об энергии, развитые английским физиком Пойнтингом в применении к электромагнитному полю, за десять лет перед этим (в 1874 г.) были высказаны русским физиком Н. А. Умовым (1846 – 1915 гг.), который вывел впервые уравнения движения энергии применительно к твёрдым и жидким телам [7].

Теорема об энергии электромагнитного поля имеет большое значение и в том отношении, что позволяет установить необходимые и достаточные условия для однозначности решений системы уравнений Максвелла.

Рассмотрим замкнутый объём 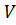, заполненный электромагнитным полем (рис. 1.12). Причём предположим, что особые точки и поверхности отсутствуют. Среда изотропная, однородная. Запишем уравнения Максвелла:

(1.52)

.

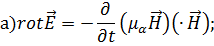
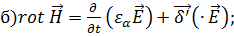
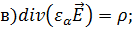
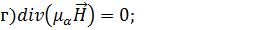
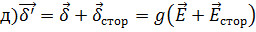Умножим скалярно первое уравнение (1.52) на 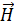, а второе уравнение на (1.50) на 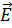и вычтем после этого из первого уравнения второе. Получим

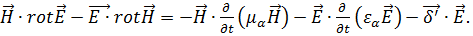(1.53)

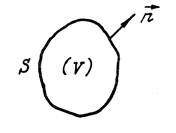
Рис.1.12

В векторном анализе доказывается, что

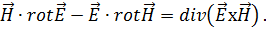
Кроме того, из уравнения (1.52 д) следует, что

.

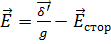Умножим скалярно на 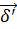, получим .

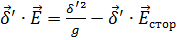Определим члены 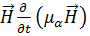и 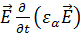. Для этого вначале найдём:

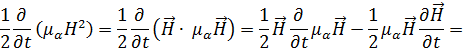
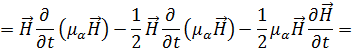
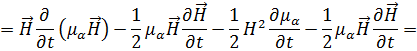
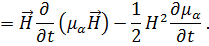
Отсюда

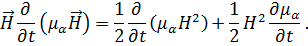
Аналогично

(1.54)

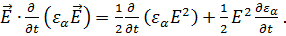
Таким образом, уравнение (1.53) принимает следующий вид:

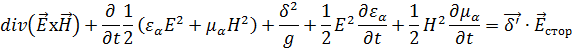
Некоторые из полученных членов в уравнении (1.54) имеют известный нам физический смысл:

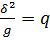– тепло, выделяющееся в единицу времени в единице объёма (закон Джоуля – Ленца);

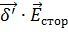– представляет работу токов сторонних сил, отнесённую к единице времени и единице объёма.

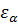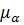Члены, зависящие от производных и по времени, определяют удельную энергию, обусловленную упругой энергией среды, энергией ориентации отдельных частиц или групп частиц, возникающую в процессе действия внешнего поля, так как в деформируемой среде величины 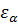и 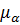зависят от величины деформации, а значит и от времени, если деформирующая сила переменная. Этими свойствами среды определяются явления электрострикции и магнитострикции.

В дальнейшем пренебрежём явлениями электрострикции и магнитострикции, так как заметно они проявляются лишь в ограниченном числе материалов. Далее мы положим, что сторонние токе в рассматриваемом объёме отсутствуют. При этих условиях уравнение (1.54) примет вид

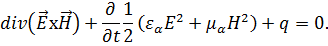
Проинтегрируем это уравнение по объёму :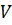

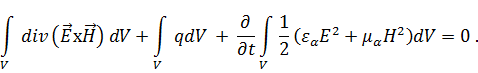
Обозначим:

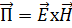– вектор Умова – Пойнтинга или вектор излучения;

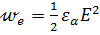– плотность электрической энергии;

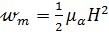– плотность магнитной энергии;

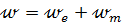– плотность электромагнитной энергии;

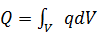– тепло, выделяемое в единицу времени во всём объёме ;

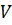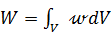– энергию, выделяемую в объёме .

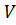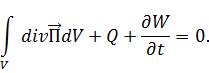Тогда

Применяя формулу Остроградского, получим:

(1.55)

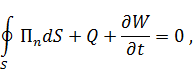
где 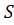– замкнутая поверхность, ограничивающая объём ;

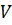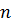– внешняя нормаль к поверхности .

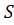Уравнение (1.55) выражает теорему об энергии электромагнитного поля при отмеченных ограничениях.

1. Предположим, что

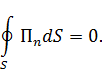
Тогда 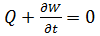или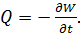

Всегда величина 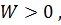так как подынтегральная функция 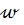квадратичная, она положительная. Поэтому в данном случае количество тепла 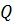(всегда 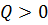), выделяемого во всём объёме 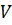в единицу времени, уравновешивается уменьшением величины 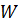в единицу времени. Следовательно, 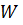можем рассматривать как меру электромагнитной энергии, за счёт уменьшения которой в единицу времени выделяется тепло .

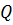2. Рассмотрим стационарный случай, когда

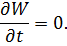
Положим, что

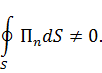
Тогда

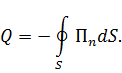
Так как всегда 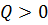, то в этом случае имеем

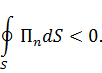
Это показывает, что тепло 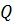в рассмотренном случае выделяется из области за счёт втекающего в эту область извне потока вектора 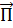. Это и позволяет рассматривать вектор 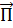как плотность потока электромагнитной энергии, поступающей в одну секунду внутрь области 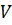через единицу поверхности, ориентированную перпендикулярно вектору 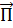и ограничивающую область 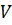. Таким образом, вектор 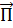есть

(1.56)

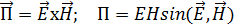, Вт/м².

Вектор Умова – Пойнтинга 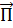– это есть энергетический вектор, определяющий поток электромагнитной энергии, пронизывающий в единицу времени (в 1 с) единичную площадку, ориентированную нормально к направлению распространения электромагнитной волны (перпендикулярно вектору ).

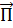3. Предположим, что область 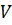ограничена непроницаемой для электромагнитного поля оболочкой, т. е. во всех точках поверхности, ограничивающей рассматриваемую область, вектор 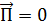. Кроме того, предположим, что в начальный момент времени ни зарядов, ни поля внутри области 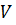не было. Тогда, как и в случае 1, имеем

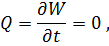
откуда следует, что

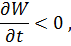
так как всегда .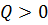

С другой стороны, всегда 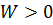. Но если производная от положительной функции по времени отрицательна, т. е. она убывает с течением времени, то наибольшим значением 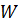будет её начальное значение, которое мы предположили равным нулю. Следовательно, при указанных предположениях всегда 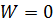. В таком случае из равенства

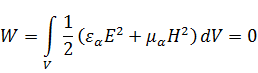
следует, что

,

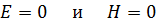так как подынтегральная квадратичная функция всегда положительна. При этом 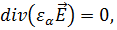т. е. 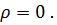Таким образом, в области 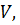ограниченной замкнутой поверхностью , электромагнитное поле может существовать только в том случае, если в начальный момент оно там было, или если вектор 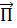на поверхности 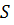отличен от нуля, т. е. внутрь области может поступать электромагнитная энергия извне.

Заметим, что этот вывод становится неверным, если внутри области 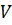находятся сторонние токи, которые могут служить источниками электромагнитного поля.

1.10. Волновые уравнения для векторов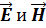

Рассмотрим волновые уравнения для случая однородной, изотропной среды. Даны уравнения Максвелла:

(1.57)

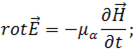
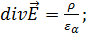
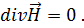
Задача заключается в решении уравнений Максвелла. Преобразуем уравнения (1.57) таким образом, чтобы получить отдельно уравнение для и отдельно уравнение для 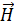[1,6]. Для этого возьмём 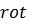от первого уравнения и, используя второе уравнение, получим:

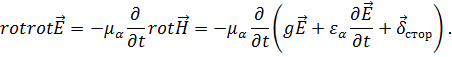
Учитывая, что 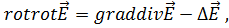соберём все члены, содержащие 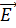в левую часть, получим:

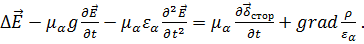(1.58)

Аналогично для 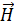. Возьмём 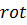от второго уравнения и, используя первое, получим:

(1.59)

Уравнение (1.58) есть волновое уравнение для вектора 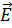, а (1.59) – волновое уравнение для вектора .

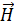Правые части уравнений (1.58) и (1.59), которые выражаются через заданные функци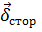и и 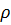, достаточно сложны. Непосредственное решение уравнений (1.58) и (1.59) встречает большие трудности. Для того чтобы облегчить решение этих уравнений, вводятся вспомогательный вектор и функция, так называемые электродинамические потенциалы. При этом уменьшается число уравнений, правая часть их упрощается. После определения вспомогательных функций и определения через них 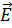и 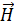, не нужно устанавливать соответствие между ними.

Вспомогательными функциями бывают вектор-потенциал и скалярный потенциал, а также вектор Герца.

Дата добавления: 2014-11-28