Лекция 20. Интегрирование рациональных и иррациональных функций. Универсальная подстановка

План:

1. Интегрирование простейших рациональных дробей.
2. Интегрирование некоторых иррациональных функций.
3. Универсальная тригонометрическая подстановка.

1. Интегрирование простейших рациональных дробей

Напомним, что функция вида Р(х)=а_ох^п+ а₁х^п-1+ а₂х^п-2+…+ а_п-1х^п+ а_п, где 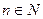, а_о, а₁…а_п – постоянные коэффициенты, называется многочленом или рациональной функцией. Число п называют степенью многочлена.

Дробно-рациональной функцией называется функция, равная отношению двух многочленов, т.е. .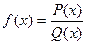

Рассмотрим некоторые простейшие интегралы от дробно-рациональных функций:

1.1. Для нахождения интегралов вида 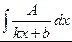(А - const) будем пользоваться интегралами от некоторых сложных функций: = .

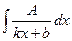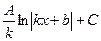Пример 20.1. Найдите интеграл .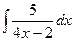

Решение. Воспользуемся приведенной выше формулой 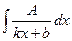= 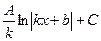. Получим, что = .

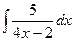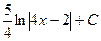1.2. Для нахождения интегралов вида 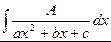(А - const) будем применять метод выделения в знаменателе полного квадрата. Исходный интеграл в результате преобразований сведется к одному из двух табличных интегралов: 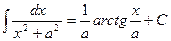или .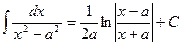

Рассмотрим вычисление таких интегралов на конкретном примере.

Пример 20.2. Найдите интеграл .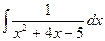

Решение. Попытаемся выделить в знаменателе полный квадрат, т.е. прийти к формуле (a ± b)² = a² ± 2ab +b².

Для этого 4 х представляем как удвоенное произведение 2∙2∙ х. Следовательно, к выражению х ² + 4 х чтобы получить полный квадрат следует добавить квадрат числа два, т.е. 4: х ² + 4 х + 4 = (х + 2)². Но, чтобы выражение в знаменателе не изменилось, нужно из (х + 2)² вычесть 4. Получим следующую цепочку преобразований:

= = .

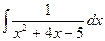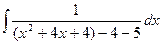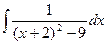Вычислим полученный интеграл методом подстановки. Положим х + 2 = и, тогда 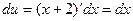. Подставим и и dx в полученный интеграл: 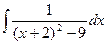= = 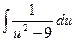. Воспользуемся табличным интегралом: 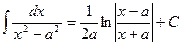, где а =3.Получим, что 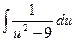= 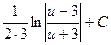. Подставим вместо и выражение х+ 2:

= = .

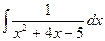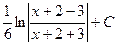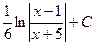Ответ: = .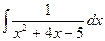

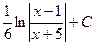1.3. Для нахождения интегралов вида 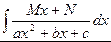(M, N - const) будем применять следующий алгоритм:

1. Выделим в знаменателе полный квадрат.

2. Выражение, стоящее в скобках, обозначим новой переменной t. Найдем х, dx и подставим их вместе с t в исходный интеграл (получим интеграл, содержащий только переменную t).

3. Разобьем полученный интеграл на сумму двух интегралов, каждый из которых вычислим отдельно: один интеграл решается методом подстановки, второй сводится к одной из формул 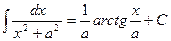или .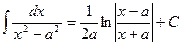

Пример 20.3. Найдите интеграл .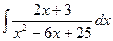

Решение. 1. Попытаемся выделить в знаменателе полный квадрат. Для этого 6 х представляем как удвоенное произведение 2∙3∙ х. Тогда к выражению х ² - 6 х следует добавить квадрат числа три, т.е. число 9: х ² – 6 х + 9 = (х - 3)². Но, чтобы выражение в знаменателе не изменилось, нужно из (х- 3)² вычесть 9. Получим цепочку преобразований:

= = .

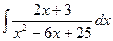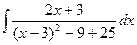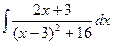2. Введем следующую подстановку: пусть х-3 = t (значит, х = t+ 3), тогда 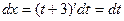. Подставим t, х, dx в интеграл :

= = = .

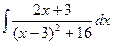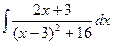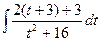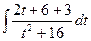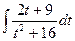3. Представим полученный интеграл как сумму двух интегралов:

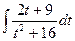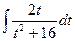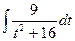= + . Найдем их отдельно.

3.1 Первый интеграл вычисляется методом подстановки. Обозначим знаменатель дроби 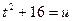, тогда 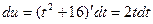. Отсюда 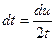. Подставляем и и dt в интеграл 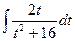и приводим его к виду: 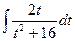= = 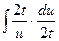= 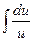ln|u|+C= =ln|t² +16 |+C. Осталось вернуться к переменной х. Поскольку 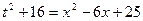, то ln|t² +16 |+C = ln|х²- 6 х +25 |+C.

3.2 Второй интеграл 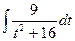вычисляется по формуле: 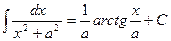(где а= 4). Тогда = = .

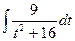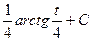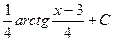3.3 Исходный интеграл 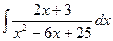равен сумме интегралов, найденных в пунктах 3.1 и 3.2: 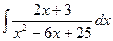= ln|х²- 6 х +25 |+ .

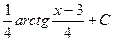Ответ: 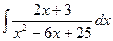= ln|х²- 6 х +25 |+ .

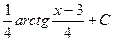Методы интегрирования других рациональных функций рассматриваются в полном курсе математического анализа (см., например, Письменный Д.Т. Конспект лекций по высшей математике, ч.1- М.:Айрис-пресс, 2006.).

1. Интегрирование некоторых иррациональных функций.

Рассмотрим нахождение неопределенных интеграл от следующих типов иррациональных функци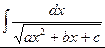й: и 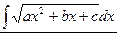(а,b,c – const). Для их нахождения будем использовать метод выделения полного квадрата в иррациональном выражении. Тогда рассматриваемые интегралы можно будет привести к видам: ,

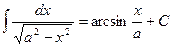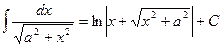или

.

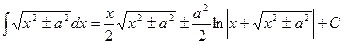Разберем нахождение интегралов от некоторых иррациональных функций на конкретных примерах.

Пример 20.4. Найдите интеграл .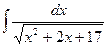

Решение. Попытаемся выделить в знаменателе полный квадрат. Для этого 2 х представляем как удвоенное произведение 2∙1∙ х. Тогда к выражению х ²+2 х следует добавить квадрат единицы (х ² + 2 х + 1 = (х + 1)²) и вычесть 1. Получим цепочку преобразований:

= = .

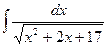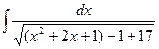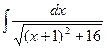Вычислим полученный интеграл методом подстановки. Положим х + 1 = и, тогда 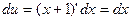. Подставим и, dx в полученный интеграл: 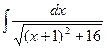= 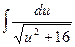. Воспользуемся табличным интегралом: 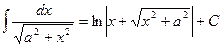, где а =4.Получим, что 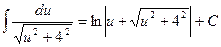. Подставим вместо и выражение х+ 1:

= .

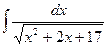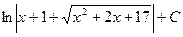Ответ: = .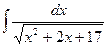

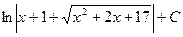Пример 20.5. Найдите интеграл .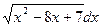

Решение. Попытаемся выделить под знаком корня полный квадрат. Для этого 8 х представляем как удвоенное произведение 2∙4∙ х. Тогда к выражению х ²-8 х следует добавить квадрат четырех (х ² - 8 х + 16 = (х - 4)²) и вычесть его. Получим цепочку преобразований:

= =

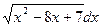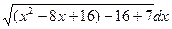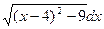
Вычислим полученный интеграл методом подстановки. Положим х - 4 = и, тогда 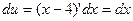. Подставим и, dx в полученный интеграл: 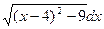= 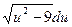. Воспользуемся табличным интегралом: 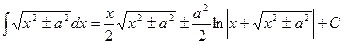, где а =3.Получим, что 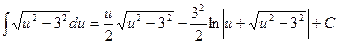. Подставим вместо и выражение х- 4:

= .

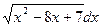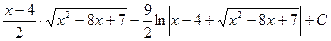Ответ: = .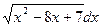

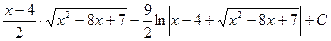1. Универсальная тригонометрическая подстановка.

Если требуется найти неопределенный интеграл от функции, содержащей sinx и cosx, которые связаны только операциями сложения, вычитания, умножения или деления, то можно использовать универсальную тригонометрическую подстановку.

Суть этой подстановки заключается в том, что sinx и cosx можно выразить через тангенс половинного угла следующим образом: 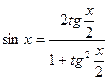, 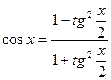. Тогда, если ввести подстановку 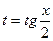, то sinx и cosx будут выражены через t следующим образом: 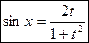, 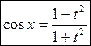. Осталось выразить х через t и найти dх.

Если 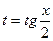, то 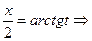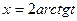. Найдем dх: = .

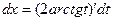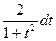Итак, для применения универсальной подстановки достаточно обозначить sinx и cosx через t (формулы выделены в рамке), а dх записать как 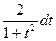. В итоге под знаком интеграла должна получиться рациональная функция, интегрирование которой рассматривалось в пункте 1. Обычно метод применения универсальной подстановки весьма громоздкий, но он всегда приводит к результату.

Рассмотрим пример применения универсальной тригонометрической подстановки.

Пример 20.6. Найдите интеграл .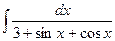

Решение. Применим универсальную подстановку 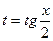, тогда 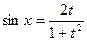, , 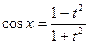dх= 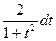. Следовательно, = = = = = .

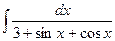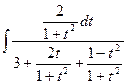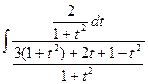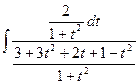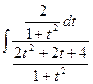Заменив дробную черту знаком ":", получим: 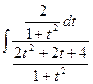= = 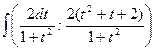= = 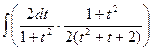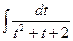. Этот интеграл решается выделением в знаменателе полного квадрата. Для этого t представляем как удвоенное произведение 2∙ 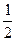∙ t. Тогда к выражению t ²+ t следует добавить квадрат одной второй (t ² + t + 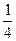= (х - 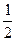)²) и вычесть его. Получим цепочку преобразований:

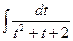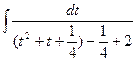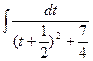= = . Вычислим полученный интеграл методом подстановки. Положим t + 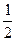= и, тогда 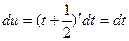. Подставим и, dt в полученный интеграл: 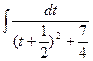= 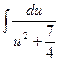. Воспользуемся табличным интегралом: 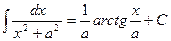, где а = 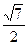. Тогда 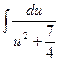= 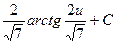. Поскольку и = t+ 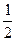, то 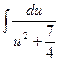= = 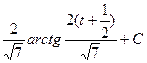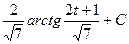. И, наконец, возвращаемся к переменной х: 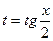. Получим, что =

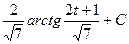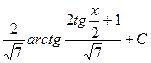
Ответ: = .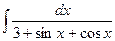

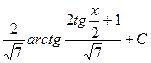Еще раз хочется отметить, что задача нахождения неопределенных интегралов от различных функций очень сложна. И хотя всякая непрерывная функция имеет первообразную (а, следовательно, и неопределенный интеграл), среди всего многообразия неопределенных интегралов лишь малая толика выражается через элементарные функции (говорят, такие интегралы " берутся ").

Существует множество интегралов, которые называют " неберущимися ". Такие интегралы не выражаются через привычные нам элементарные функции. Так, например, нельзя взять интеграл 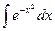, т.к. не существует элементарной функции, производная которой была бы равна 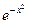. Но некоторые из "неберущихся" интегралов имеют большое прикладное значение. Так интеграл 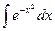называют интегралом Пуассона и широко применяют в теории вероятностей.

Существуют и другие важные "неберущиеся" интегралы: 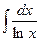- интегральный логарифм (применяется в теории чисел), 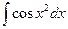и - и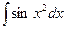нтегралы Френеля (применяются в физике). Для них составлены подробные таблицы значений при различных значениях аргумента х.

Контрольные вопросы:

1. Какими методами находятся интегралы от следующих видов дробно-рациональных функций: , , ?
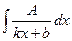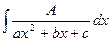2. В чем сущность интегрирования некоторых иррациональных функций 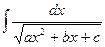и ?
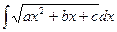3. Когда применяется универсальная тригонометрическая подстановка? Можно ли ее применить для нахождения интеграла вида ?
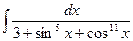4. Любой ли интеграл может быть выражен с помощью конечного числа элементарных функций?

Дата добавления: 2014-12-27