Неопределённых интегралов

Лекция 19. ОСНОВНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ

План:

1. Непосредственное интегрирование.

2. Интегралы от некоторых сложных функций.

3. Интегрирование методом замены переменной (методом подстановки).

4. Метод интегрирования по частям.

1. Непосредственное интегрирование

Под непосредственным интегрированием понимают такой способ интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции и применения свойств неопределенного интеграла приводится к одному или нескольким табличным интегралам.

Пример 19.1. Найдите .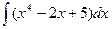

Решение. Воспользуемся свойствами неопределенного интеграла: представим интеграл как сумму и разность соответствующих интегралов:

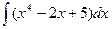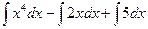= . Вынесем константы за знак интеграла:

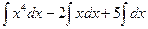и воспользуемся табличными интегралами. Получим, что = = .

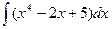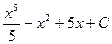Пример 19.2. Найдите .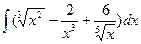

Решение. Каждое слагаемое, стоящее под знаком интеграла, представим в виде степени с рациональным показателем. Для этого применим следующие свойства степени: а^-п = 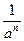; 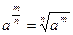. Тогда

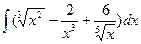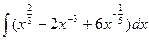= . Представим данный интеграл как сумму и разность интегралов, вынесем константы за знак интеграла:

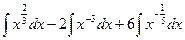. Воспользовавшись табличным интегралом 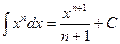, получим: = = = = = =

= = .

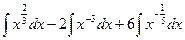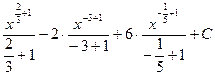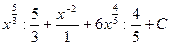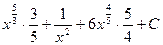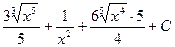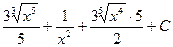Пример 19.3. Найдите .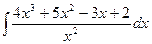

Решение. Разделив почленно числитель на знаменатель, получим = = .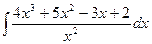

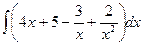Представим данный интеграл как сумму и разность интегралов, вынесем константы за скобки:

= = .

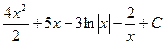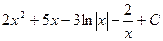Пример 19.4. Найти .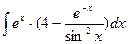

Решение. Раскрывая скобки и применяя табличные интегралы, получим:

= = = .

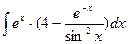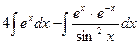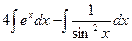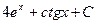1. Интегралы от некоторых сложных функций

Некоторыми сложными функциями будем считать функции вида f(kx+b), где k и b – любые действительные числа. Так, 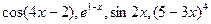- примеры некоторых сложных функций. В аргументе этих функций переменная х находится только в первой степени!

Для нахождения интеграла от некоторых сложных функций будем использовать формулу: 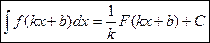. Ее правильность легко проверяется дифференцированием обеих частей.

Можно также применять следующий алгоритм:

1. Выбрать табличный интеграл, к которому сведется данный.

2. Вместо х в табличном интеграле подставить выражение kх+b из исходного интеграла.

3. В правую часть добавить множитель 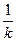, где k – коэффициент перед х.

Рассмотрим нахождение интеграла от некоторых сложных функций на примерах.

Пример 19.4. Найдите .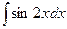

Решение. Видим, что под знаком интеграла стоит некоторая сложная функция. Воспользуемся табличным интегралом .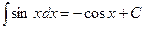

В нашем примере в качестве аргумента выступает угол 2 х, Выделим коэффициент k, стоящий перед х: k= 2, следовательно, в правую часть мы должны добавить множитель 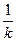, то есть 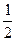. Тогда получим, что .

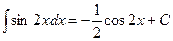Пример 19.5. Найдите .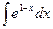

Решение. Под знаком интеграла стоит некоторая сложная функция. Воспользуемся табличным интегралом .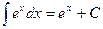

В примере в качестве аргумента выступает выражение 1- х. Выделим коэффициент k, стоящий перед х: k= -1, следовательно, в правую часть добавим множитель (-1). Тогда получим, что .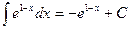

Пример 19.6. Найдите .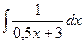

Решение. Под знаком интеграла стоит некоторая сложная функция. Воспользуемся табличным интегралом .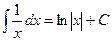

В примере в качестве аргумента выступает выражение 0,5 х+ 3. Выделим коэффициент k, стоящий перед х: k=0,5, следовательно, в правую часть добавим множитель 1:0,5=2. Тогда получим, что .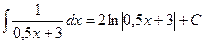

Пример 19.7. Найдите .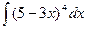

Решение. Под знаком интеграла стоит некоторая сложная функция. Воспользуемся табличным интегралом .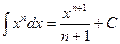

В примере в качестве аргумента выступает выражение 5-3 х. Выделим коэффициент k, стоящий перед х: k=- 3, следовательно, в правую часть добавим множитель (-1/3). Тогда получим, что = .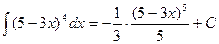

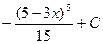1. Интегрирование методом замены переменной (методом подстановки).

Вычислить заданный интеграл непосредственным интегрированием или взятием его как интеграла от некоторой сложной функции удается далеко не всегда. Одним из наиболее эффективных приемов является метод подстановки. Сущность этого метода заключается в том, что путем введения новой переменной удаётся свести заданный интеграл к новому интегралу, который чаще всего является табличным.

В основе метода подстановки лежит утверждение, являющееся следствием правила дифференцирования производной сложной функции. Пусть задана сложная функция y=f(g(x)). Тогда исходный интеграл можно привести к виду: 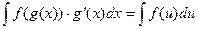. Эта формула называется формулой замены переменных в неопределенном интеграле.

Приведем алгоритм нахождения неопределенного интеграла методом замены переменной.

1. Введем новую переменную u таким образом, чтобы под знаком интеграла стояла функция, содержащая и, и производная и (u=g(x)).
2. Найдем du по формуле: du=и'dx.
3. Выразим dx через du (при этом помним, что если множитель в одной части формулы находился в числителе, то в другую часть он перейдет в знаменатель и наоборот: если множитель находился в знаменателе, то в другую часть он перейдет в числитель).
4. Подставим и и dx в исходный интеграл. Если подстановка выполнена верно, то произойдет сокращение одинаковых множителей и интеграл сведется к табличному относительно переменной и: .
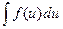5. Вычислить интеграл с переменной и.
6. Перейти от переменной интегрирования и к исходной переменной х.

Рассмотрим применение метода подстановки на конкретных примерах.

Пример 19.8. Найдите .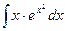

Решение. 1. Выполним подстановку u=х² с целью прийти к интегралу от функции е^и.

2. Найдем du по формуле du=и'dx: du=(х²)'dx =2хdx.

3. Выразим dx из выражения пункта 2 (du=2хdx): .

4. Подставим и и dx в исходный интеграл: 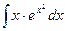= 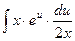. Видим, что х можно сократить и прийти к интегралу относительно переменной и: .

5. Для нахождения полученного интеграла константу 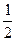вынесем за знак интеграла: 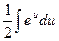. По таблице неопределенных интегралов находим, что = .

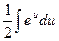6. Поскольку u=х², = = .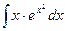

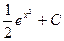Ответ: =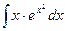

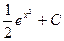
Пример 19.9. Найдите .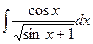

Решение. 1. Выполним подстановку u= . Тогда под знаком интеграла будет стоять функция от u (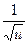) и производная u (u'=cosx).

2. Найдем du по формуле du=и'dx: du= () ' dx = cosхdx.

3. Выразим dx из выражения пункта 2 (du=cosхdx): .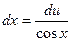

4. Подставим и и dx в исходный интеграл: 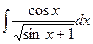= 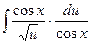. Видим, что cosх можно сократить и прийти к интегралу относительно переменной и: .

5. По таблице неопределенных интегралов находим, что = .

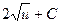6. Поскольку u= , = = .

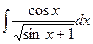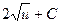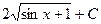Ответ: = .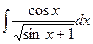

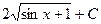1. Метод интегрирования по частям

Сущность метода интегрирования по частям вполне соответствует его названию. Дело в том, что при вычислении интеграла этим методом подынтегральное выражение 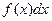представляют в виде произведения двух множителей u и dv, причем dх обязательно входит в dv. Далее пользуются формулой интегрирования по частям:

.

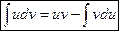При вычислении интегралов методом по частям главным является разумное разбиение подынтегрального выражения на u и dv. Укажем некоторые типы интегралов, которые удобно вычислять методом интегрирования по частям:

1. Если под знаком интеграла встречается логарифмическая или обратные тригонометрические функции (arcsinx, arccosx, arctgx, arcctgx), то их обозначают за и, остальные множители – за dv.

2. В интегралах вида 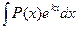, , 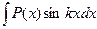, 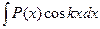где Р(х) – многочлен, k -const, за и принимают многочлен Р(х), остальные множители – за dv.

Для нахождения неопределенного интеграла методом по частям можно использовать следующий алгоритм:

1. Разбиваем подынтегральное выражение на u и dv (в соответствии с правилом, рассмотренным выше).

2. Находим dи=и'dx и .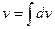

3. Подставляем u, v, dи и dv в формулу 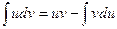и вычисляем получившийся интеграл.

Рассмотрим применение метода интегрирования по частям на примерах.

Пример 19.10. Найдите .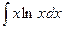

Решение. 1. Поскольку под знаком интеграла встречается логарифмическая функция, то ее принимаем за u: u=lnx. Остальные множители принимаем за dv: dv=хdx.

2. Находим dи=и'dx: dи=(lnx)'dx= .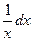

Находим 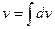: 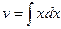= 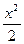(полагаем С =0).

3. Воспользуемся формулой 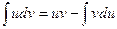: 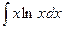= lnx∙ 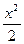- 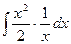= =lnx∙ - = .

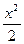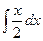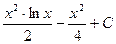Ответ: = .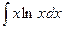

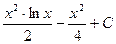Пример 19.11. Найдите .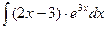

Решение. 1. Исходный интеграл имеет вид 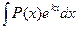, следовательно, за и принимают многочлен (и=2х-3), остальные множители – за dv: dv=е^3хdx.

2. Находим dи=и'dx: dи=(2х-3)'dx=2dx.

Находим 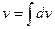: 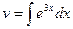= (полагаем С =0).

3. По формуле 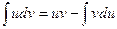имеем: 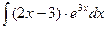= (2х-3)∙ - = = .

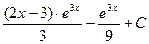Ответ: = .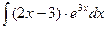

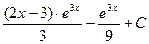Контрольные вопросы:

1. Какие основные методы интегрирования существуют?
2. Что называют непосредственным интегрированием?
3. Как вычисляются интегралы от некоторых сложных функций?
4. В чем заключается сущность метода интегрирования подстановкой?
5. В чем сущность метода интегрирования по частям?

Дата добавления: 2014-12-27