Лекция 21. Определенный интеграл

План:

1. Понятие определенного интеграла.
2. Основные свойства определенного интеграла.
3. Формула Ньютона-Лейбница.

1. Понятие определенного интеграла.

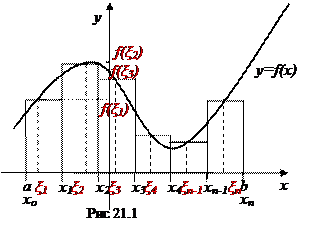Пусть функция y=f(x) определена на отрезке [ a;b ].

Выполним следующие действия (рис. 21.1).

1. С помощью точек х_о=а, х₁, х₂,…, х_п=b разобьём отрезок [ a;b ] на п частей (х_о<х₁<х₂<…<х_п). Длину первого отрезка обозначим Δ х₁, второго – Δ х₂…, п- го – Δ х_п.

2. Внутри каждого отрезка [ х_о;х₁ ], [ х₁;х₂ ] …

[ х_п-1;х_п ] выберем соответственно произвольные точки ξ₁, ξ₂,…, ξ _п.

3. Найдем значения функции в точках ξ₁, ξ₂,…, ξ _п: f (ξ₁), f (ξ₂),…, f (ξ _п).

4. Для каждого промежутка умножим найденное значение функции f (ξ _i) (где i =1,2,…, п) на длину соответствующего отрезка Δ х_i: f (ξ _i)∙ Δ х_i.

5. Составим сумму Sn всех таких произведений: Sn= f (ξ ₁)∙ Δ х₁+ f (ξ ₂)∙ Δ х₂+…+ f (ξ _п)∙ Δ х_п. Эту сумму можно записать в виде: Sn= 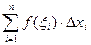. Такую сумму называют интегральной суммой функции y=f(x) на отрезке [ a;b ].

Если на отрезке [ a;b ] функция y=f(x) принимает неотрицательные значения, то каждое слагаемое интегральной суммы равно площади прямоугольника с основанием Δ х_i и высотой f (ξ _i). А вся сумма Sn равна площади "ступенчатой фигуры", получающейся объединением рассматриваемых прямоугольников.

Мы разбивали отрезок [ a;b ] на произвольное число частей, точку ξ _i внутри каждого отрезка также выбирали произвольно. Очевидно, что при различных разбиениях отрезка [ a;b ] на части и различном выборе точек ξ _i можно составить бесконечное число интегральных сумм.

Найдем предел интегральной суммы Sn при п , но при условии, что длина самого большого среди отрезков Δ х_i (λ=maxΔ х_i, где i =1,2,…, п) будет стремиться к нулю, т.е. λ→0.

Если при п и λ→0 интегральная сумма Sn имеет предел А, который не зависит ни от способа разбиения отрезка [ a;b ] на части, ни от выбора точек ξ _i, то число А называется определенным интегралом от функции f(x) на отрезке [ a;b ] и обозначается .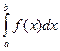

Таким образом, = .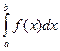

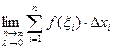Числа а и b называются соответственно нижней и верхней границами интегрирования, f(x) - подынтегральной функцией, f(x)dx – подынтегральным выражением, х - переменной интегрирования, отрезок [ a;b ] – областью (отрезком) интегрирования.

Функция f(x), для которой на отрезке [ a;b ] существует определенный интеграл, называется интегрируемой на этом отрезке.

Сформулируем теорему существования определенного интеграла.

Теорема (Коши). Если функция у=f(x) непрерывна на отрезке [ a;b ], то определенный интеграл 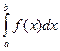существует.

1. Основные свойства определенного интеграла.

Рассмотрим основные свойства определенного интеграла, считая функцию у=f(x), непрерывной (и, следовательно, интегрируемой) на отрезке [ a;b ].

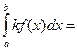
1. Постоянный множитель можно выносить за знак определенного интеграла: (k – const).

Докажем это свойство. По определению 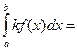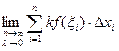= = k 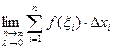= , что и требовалось доказать.

1. Определенный интеграл от алгебраической суммы двух функций равен алгебраической сумме их интегралов: = ± .
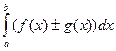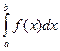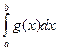2. Границы интегрирования можно менять местами, при этом знак "минус" выносится вперед: = .

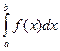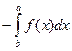Свойства 1, 2 и 3 широко применяются при вычислении определенных интегралов.

1. Определенный интеграл с одинаковыми пределами интегрирования равен нулю: .
2. Если функция у=f(x) интегрируема на отрезке [ a;b ] и a<c<b, то справедливо равенство: = + .

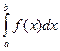Это означает, что интеграл по всему отрезку равен сумме интегралов по его частям. Данное свойство называют свойством аддитивности определенного интеграла.

1. Если функция f(x) сохраняет знак на отрезке [ a;b ] (a<b), то интеграл 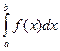имеет тот же знак, что и функция f(x). Так, если f(x)≥ 0 на отрезке [ a;b ], то и 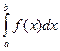≥ 0.
2. Неравенство между интегрируемыми функциями на отрезке [ a;b ] (a<b) можно интегрировать: например, если f(x)≥g(x) при [ a;b ], то ≥ .

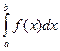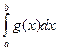1. Формула Ньютона-Лейбница

Рассмотрим функцию у=f(x), непрерывную на отрезке [ a;b ]. Пусть F(x) – какая либо первообразная f(x) на отрезке [ a;b ]. Тогда имеет место формула, получившая название формула Ньютона-Лейбница: = .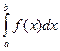

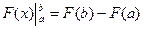Формула Ньютона-Лейбница даёт удобный способ вычисления определенного интеграла. Чтобы вычислить определенный интеграл от непрерывной на отрезке [ a;b ] функции, нужно:

1. Найти неопределенный интеграл от функции f(x), выбрав С =0. Справа поставить вертикальную черту, рядом с которой указать верхнюю и нижнюю границы интегрирования.
2. В полученное выражение вместо х следует подставить сначала верхнюю границу b, поставить знак "минус", подставить в выражение вместо х нижнюю границу а.

Отметим, что неопределенный интеграл от непрерывной функции f(x) – множество функций, отличающихся друг от друга на число С, а определенный интеграл от непрерывной функции f(x) – действительное число.

Рассмотрим пример вычисления определенных интегралов с помощью формулы Ньютона-Лейбница.

Пример 21.1. Вычислите .

Решение. Сначала найдем неопределенный интеграл от заданной функции, выбрав С =0 и добавив границы интегрирования: = .

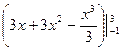Подставим сначала верхнюю, потом нижнюю границы интегрирования: 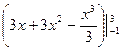= 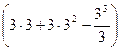- 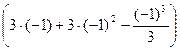=9+27-9- 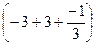= = . Ответ: = .

Контрольные вопросы:

1. Что называют интегральной суммой функции y=f(x) на отрезке [ a;b ]? Сколько интегральных сумм для данной функции на отрезке [ a;b ] можно составить?

2. Что называют определенным интегралом ?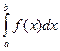

3. Какими свойствами обладает определенный интеграл?

4. Для чего служит формула Ньютона-Лейбница?

5. Какова глобальные отличия определенного интеграла от неопределенного?

Дата добавления: 2014-12-27