Теорема о необходимых и достаточных условиях оптимальности смешанных стратегий. Метод сведения решения игр к решению задачи линейного программирования

Транспортная задача незамкнутого типа. Постановка, способ сведения к задаче замкнутого типа(с обоснованием). Алгоритм решения.

Задача максимизации прибыли при заданных ценах на продукцию и ресурсы. Анализ оптимальных решений с помощью множителей Лагранжа.

Пусть производится один продукт ценой P ₀, используются ресурсы с ценами 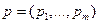. Требуется решить задачу максимизации прибыли при заданных P ₀ и p:

max (P ₀ f (x) – < p, x >) (1)

x ³ 0 (2)

Исследование задачи будем проводить с помощью функции Лагранжа:

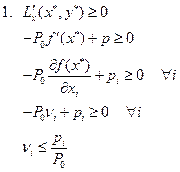
– балансовое соотношение

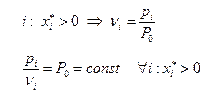
В оптимальном плане x ^* для любых используемых ресурсов отношение цены к предельной эффективности постоянно. Для этих же ресурсов показали, что соотношение предельных эффективностей равно соотношению цен. Наибольшая отдача будет от тех ресурсов, которые имеют самую большую предельную эффективность в текущей точке.

Эти свойства не имеют универсального значения. Они применимы только тогда, когда эффективность ресурса при увеличении масштаба производства сокращается. При этой ситуации нахождение оптимального плана задачи (1)-(2) можно интерпретировать как процесс выравнивания соотношения цен и предельных эффективностей.

Предельная эффективность 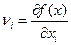– показывает предельный прирост выпуска продукции при увеличении затрат i -го ресурса на малую величину.

23. Транспортная задача замкнутого типа: постановка, существование решения, метод потенциалов.

Формулировка транспортной задачи (ТЗ): имеется m поставщиков (пунктов отправления) А₁, …, A_m, у которых имеется однородный груз в кол-вах а₁, …, а_m. В этом товаре нуждается n потребителей В₁, …, В_n, каждый в кол-ве b₁, …, b_n. Т.ж. известны так называемые коэф-ты затрат с_ij = стоимости перевозки груза от постав А_i к потреб В_j. Данные удобно записывать в распределительной матрице:

потр пост	В1	…	Вn
b1	…	bn
А1	а1	с11 х11	…	с1n х1n
…	…	…	…	…
Am	аm	сm1 хm1	…	сmn хmn

Постановка ТЗ: необходимо найти такой план перевозок, чтобы:

1) мощности всех поставщиков были реализованы

2) спрос всех потребителей был удовлетворителен

3) суммарные затраты на перевозки были мин-ми

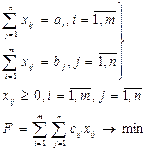Составим эк-ко-мат-ую модель ТЗ, т.е. запишем на мат-ом языке зад-ые усл-ия. Обоз-им ч/з х_ij – кол-во ед-ц груза, к-ый необх. доставить от поставщика а_i к потребителю b_j. Матрица, сост-щая из х_ij наз-ся матрицей перевозок, а из с_ij – матрицей тарифов.

Мощности всех поставщиков д.б. реализованы

(1)

Спрос всех потреб-лей д.б. удовл-н

(2) По смыслу поставка не м.б. отр-ной

(3) Суммарные затраты на перевозку
ТЗ закл-ся в нах-ии х_ij, удовл-щие (1), (2), при к-ых (3) принимает наим-ее значение.

План перевозок х наз-ся допустимым, если он удовл-ет (1) и (2). Распред-ие поставок наз-ся оптимальным, если оно доставляет мин-м (3).

Т. о сущ-ии допустимого плана: для того, чтобы ТЗ имела допустимый план необх. и дост., чтобы ТЗ была закрытой , т.е. суммарная мощность поставщиков совпадала с суммарным спросом потребителей.

Т. о ранге матрицы: Ранг матрицы коэф-тов системы (1) = m+n-1. (Если спросят написать):

Решение закрытой ТЗ:

1. нах-ся любое допустимое распред-ие поставок
2. это распред-ие перестр-ся, чтобы мин-ть затраты

1. н-р, эту з-чу м. решить с пом. мет. наим. затрат. Согласно этому мет. В нач. дается макс-но возм-ная поставка в клетку с наим-им коэф-том затрат. Эту клетку сч-т заполненной, для удобства перечерк-т сплошной линией. Выпавшие из дальнейшего рассм-ия клетки наз-т свободными и перечер-т пунктирными линиями. Затем процедура повт-ся в непрочер-ых никакими линиями клетках. После этого дел-ся проверка: кол-во заполн-х клеток д. = m+n-1. Если их меньше, то вводим фиктивные нулевые поставки до треб-го кол-ва. Вводят их т.о., чтобы не образ-ся квадрат или прямоугольник из заполн-ых клеток (иначе невозм-но будет найти потенциал).

2. м-д потенциалов.

Он основан на Т. о потенциалах: Если х^* есть оптимальный план поставок, то ему соотв-т система чисел (u_i^*,v_j^*), i=1,m,j=1,n, наз-ых потенциалами строк и столбцов (поставщиков и потребителей), удовл-щих усл-ию:

Исп-уя эту теорему, мы м. найти эти числа. Для этого u₁ полагают =0 (м. = любому числу), остальные потенциалы нах-ся по заполненным клеткам по след-щей ф-ле: .

После того, как были найдены все потенциалы нах-т Эл-ты матрицы оценок по ф-ле: .

Для заполн-ых клеток эл-ты этой матрицы =0. Если для незапол-ых клеток все >=0, то по теореме мы нах-м оптимальное распред-ие. Если же среди оценок есть отриц-ые, то распред-ие точно не оптимальное и перераспред-т поставки, а именно строят цикл пересчета. Для этого берут любую свободную клетку с отриц-ой оценкой наз-т вершиной цикла, далее двиг-ся по некот-ым заполн-ым клеткам так, чтобы вернуться назад, двиг-ся под прямыми углами. В одной строчке или столбце м.б. лишь одно звено.

Вершине цикла усл-но ставим «+», затем знаки черед-ся(в цикле всегда четное кол-во клеток). Затем из тех клеток, где «-» выбираем наим-ую поставку и ее вычитаем из всех клеток, где «-», и прибавляем, где «+». Измененные значения цикла вставляем в исходную таблицу и снова нах-м потенциалы и матрицы оценок.

Альтернативное решение.

Если оценка получается в оптимальном решении =0 в свободной клетке. Выбираем вершину, создаем цикл, получаем новое решение и составляем выпуклую линейную комбинацию вида:

Формулировка транспортной задачи (ТЗ): имеется m поставщиков (пунктов отправления) А₁, …, A_m, у кот-ых имеется однородный груз в кол-вах а₁, …, а_m. В этом товаре нуждается n потребителей В₁, …, В_n, каждый в кол-ве b₁, …, b_n. Т.ж. изв-ны так наз-ые коэф-ты затрат с_ij = стоимости перевозки груза от постав А_i к потреб В_j. Данные удобно записывать в распределительной матрице:

потр пост	В1	…	Вn
b1	…	bn
А1	а1	с11 х11	…	с1n х1n
…	…	…	…	…
Am	аm	сm1 хm1	…	сmn хmn

Постановка ТЗ: необх. найти такой план перевозок, чтобы:

4) мощности всех поставщиков были реализованы

5) спрос всех потребителей был удовлет-н

6) суммарные затраты на перевозки были мин-ми

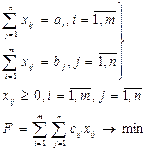Составим эк-ко-мат-ую модель ТЗ, т.е. запишем на мат-ом языке зад-ые усл-ия. Обоз-им ч/з х_ij – кол-во ед-ц груза, к-ый необх. доставить от пост-ка а_i к потр-лю b_j. М-ца, сост-щая из х_ij наз-ся м-цей перевозок, а из с_ij – м-цей тарифов.

Мощности всех пост-ков д.б. реализованы

(1)

Спрос всех потреб-лей д.б. удовл-н

(2) По смыслу поставка не м.б. отр-ной

(3) Суммарные затраты на перевозку
ТЗ закл-ся в нах-ии х_ij, удовл-щие (1), (2), при к-ых (3) принимает наим-ее зн-ие.

План перевозок х наз-ся допустимым, если он удовл-ет (1) и (2). Распред-ие поставок наз-ся оптим-ым, если оно доставляет мин-м (3).

Т. о сущ-ии допустимого плана: для того, чтобы ТЗ имела допустимый план необх. и дост., чтобы ТЗ была закрытой , т.е. суммарная мощность пост-ков совпадала с суммарным спросом потр-лей.

ТЗ наз-ся открытой, если суммарная мощность пост-ков не совпадает с суммарным спросом потр-лей.

Для реш-ия з-чи открытого типа необх. свести ее к закрытому типу. Обоснованием для сведения является теорема о сущ-ии допустимого плана.

Предпол-им, что сум-ая мощность пост-ка превышает сум-ый спрос потр-ля, т.е. . В этом случ. необ. ввести нового фиктивного потр-ля В_n+1 со спросом . Обычно коэф-ты затрат = 0, но в жизни это м.б. склад и, след-но, затраты на хр-ие ≠0.

Если сум-ая мощность пост-ков меньше сум-го спроса потр-лей, т.е. , то вводят фиктивного пост-ка A_m+1 с мощностью: 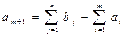. Обычно коэф-ты затрат = 0, но в жизни фиктивного поставщика нет. И для того чтобы его исключить плана, необх. поставить ему большие коэф-ты.

Т. о ранге м-цы: Ранг м-цы коэф-тов системы (1) = m+n-1. (Если спросят написать):

Реш-ие закрытой ТЗ:

1. нах-ся любое допустимое распред-ие поставок
2. это распред-ие перестр-ся, чтобы мин-ть затраты

3. н-р, эту з-чу м. решить с пом. мет. наим. затрат. Согласно этому мет. в нач. дается макс-но возм-ная поставка в клетку с наим-им коэф-том затрат. Эту клетку сч-т заполненной, для удобства перечерк-т сплошной линией. Выпавшие из дальнейшего рассм-ия клетки наз-т свободными и перечер-т пунктирными линиями. Затем процедура повт-ся в непрочер-ых никакими линиями клетках. После этого дел-ся проверка: кол-во заполн-х клеток д. = m+n-1. Если их меньше, то вводим фиктивные нулевые поставки до треб-го кол-ва. Вводят их т.о., чтобы не образ-ся квадрат или прямоугольник из заполн-ых клеток (иначе невозм-но будет найти потенциал).

4. м-д потенциалов.

Он основан на Т. о потенциалах: Если х^* есть оптим-ый план поставок, то ему соотв-т система чисел (u_i^*,v_j^*), i=1,m,j=1,n, наз-ых потенциалами строк и столбцов (пост-ков и потр-лей), удовл-щих усл-ию:

Исп-уя эту теорему, мы м. найти эти числа. Для этого u₁ полагают =0 (м. = любому числу), остальные потенциалы нах-ся по заполненным клеткам по след-щей ф-ле: .

После того, как были найдены все потенциалы нах-т Эл-ты м-цы оценок по ф-ле: .

Для заполн-ых клеток эл-ты этой м-цы =0. Если для незапол-ых клеток все >=0, то по теореме мы нах-м оптим-ое распред-ие. Если же среди оценок есть отриц-ые, то распред-ие точно не оптим-ое и перераспред-т поставки, а именно строят цикл пересчета. Для этого берут любую свободную клетку с отриц-ой оценкой наз-т вершиной цикла, далее двиг-ся по некот-ым заполн-ым клеткам так, чтобы вернуться назад, двиг-ся под прямыми углами. В одной строчке или столбце м.б. лишь одно звено.

Вершине цикла усл-но ставим «+», затем знаки черед-ся(в цикле всегда четное кол-во клеток). Затем из тех клеток, где «-» выбираем наим-ую поставку и ее вычитаем из всех клеток, где «-», и прибавляем, где «+». Измененные зн-ия цикла вставляем в исх-ую таблицу и снова нах-м потенциалы и м-цы оценок.

Альтерн-ое реш-ие.

Если оценка получается в оптим-ом реш-ии =0 в свободной клетке. Выбираем вершину, создаем цикл, получаем новое реш-ие и составляем выпуклую лин-ую комбинацию вида:

Игрой наз-ся процесс, при кот-ром каждый из игроков выбирает себе стратегию и в возникшей ситуации получает выигрыш.

Седловой точкой функции f(x,y), опред-ной на множ-ве X (множ-во стратегий первого игрока) Y(множество стратегий второго игрока), наз-ся пара (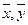) такая, что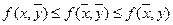

Значение функции выигрыша в седловой точке называется ценой игры.

Т. [о необходимых и достаточных условиях оптимальности смешанных стратегий]

Пусть игра определена матрицей 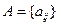и ценой игры V. Для того, чтобы смешанная стратегия 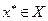была оптимальной стратегией 1-го игрока 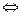выполнение следующего неравенства:

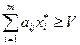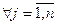, (1)

Для того, чтобы смешанная стратегия 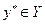была оптимальной стратегией 2-го игрока 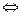выполнение следующего неравенства:

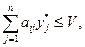
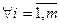(2).

Док-во: Рассмотрим с точки зрения 2-го игрока.

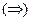
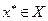– оптимальная стратегия 1 игрока 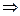х ^* является первой координатой некоторой седловой точки ф-ции выигрыша М (х, у). Тогда по определению седловой точки:

, .

.

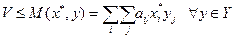Так как это неравенство выполняется для , то оно выполняется и для k = 1..n.

Остается к=1,n. ЧТД.

Вып-ся (1):

, .

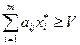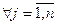Выделим смешанную стратегию . Умножим каждое j неравенство на у_j и просуммируем. Эти у – неотр.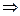

.

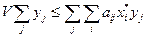
эта функция имеет седловую точку, выберем седловую точку (). Для нее вып-ся: . Следовательно

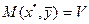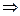В таком случае (по следствию Т о седловой точке) для х, у , седловая точка х ^* – оптимальная стратегия для 1 игр. ЧТД.

СЛЕДСТВИЕ: Если для смешанных стратегий (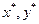) и числа V одновременно выполняются (1) и (2), то (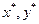) будут оптимальными стратегиями игроков, а V – цена игры.

Док-во: умножим (1) на y и просуммируем:

умножим (2) на x и просуммируем:

Получаем

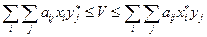
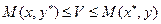
Тогда по следствию Т о седловой точке точка (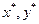) – седловая и 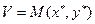– цена игры.

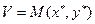следует из того, что последнее неравенство выполняется для ; если подставить , то получим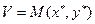

ЧТД.

Метод сведения решения игр к решению задачи линейного программирования. (I метод)

Пусть игра определена матрицей 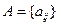и ценой игры V. По следствию теоремы

Если для смешанных стратегий (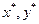) и числа V одновременно выполняются (1) и (2), то

– оптимальные стратегии игроков (*)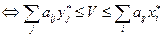

Требуется, чтобы V > 0. Если все a_ij > 0, то V > 0. Если $ a_ij < 0, то ко всем a_ij прибавляем |min a_ij |, тогда получим эквивалентные игры, то есть новое V = V +|min a_ij |, а стратегии те же.

1) Рассмотрим левую часть:

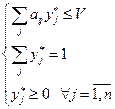
V > 0 необходимо здесь, чтобы не менялся знак, так как делим на V.

Обозначим , тогда

решение систем равенств и неравенств – задача оптимизации с целевой функцией, составленной с помощью одного равенства/неравенства и систем ограничений в виде других равенств/неравенств:

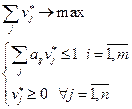(1)

На max, потому что стратегия 2-го игрока

2) Рассмотрим правую часть (аналогично):

разделим на V > 0: (2)

Задачи (1) и (2) – двойственные, т.е. решение одной можно найти из решения другой (в последней симплекс-таблице в строке оценок). Значения линейных форм совпадут:

Обозначим некоторое число (3)

И в качестве 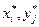возьмем 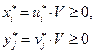(4)

Покажем, что 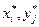– компоненты оптимальных смешанных стратегий игроков, а число V – цена игры с матрицей A.

– смешанные стратегии. Покажем оптимальность:

Умножив неравенства задач (1) и (2) на V получим (*) при полученных нами – оптимальное решение, а V – цена игры.

Алгоритм:

1. по матрице А составить (1) и (2)

2. найти решения

3. по (3) найти цену игры, по (4) оптимальные стратегии.

Дата добавления: 2015-01-03