Суть метода

Метод покоординатного спуска

Когда остановится?

Останавливаемся, когда либо 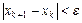, либо , где - наперед заданные малые положительные числа.

Но если функция имеет достаточно простой вид, то необходимым и достаточным условием оптимальности решения является равенство нулю градиента в т. (это действительно и для сложной функции, однако уравнение, где градиент =0 не решаемое).

Пусть имеется выпуклая функция 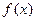и задача 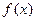на минимум.

Берем любую начальную точку и двигаемся от нее с некоторым шагом вдоль первой координатной оси. Вычисляем значение функции в новой точке. Если оно меньше, чем в начальной, то переходим к этой точке. Иначе двигаемся в противоположную сторону. Вычисляем значение функции в этой точке, если меньше, то ее берем за новую, если нет, то от исходной точки двигаемся вдоль другой оси, до тех пор, пока не попадем в новую точку. Если попали в новую точку, то процедуру повторяем. Если не попали в новую точку, то изменяем шаг. Как правило, его уменьшаем.

Опишем вышесказанное с помощью формул.

Обозначим - координатный (единичный) вектор, у которого на -ом месте стоит 1.

Пусть точка 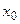есть начальная точка. - некоторое положительное число, называемое параметром метода.

Предположим . (1)

Полагаем . (2)

Условие (2) обеспечивает циклический перебор векторов , т.е. .

Вычисляем значение функции 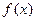в точке 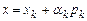и проверяем неравенство . (3)

Если (3) выполняется, то полагаем

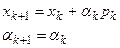(4)

Если (3) не выполняется, то вычисляем значение функции 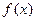в точке 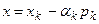и проверяем . (5)

В случае выполнения (5) полагаем

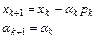(6)

Назовем 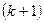-ую итерацию удачной, если справедливо либо (3), либо (5). Если 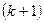-ая итерация будет неудачной, то необходимо некоторым образом изменить шаг, т.е. параметр метода, а именно полагаем:

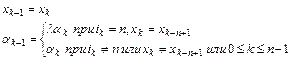(7)

Здесь - фиксированное число, являющееся параметром метода.

Условие (7) означает, что если за один цикл из n итераций при переборе всех координатных осей с шагом имеется хотя бы одна удачная итерация, то длина шага не дробится и сохраняется, по крайней мере, в следующем цикле из n итераций. Если же среди последних n итераций не оказалось ни одной удачной, то шаг дробится.

Теорема (о сходимости метода координатного спуска).

Пусть функция 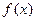выпуклая и имеет непрерывную производную, тогда последовательность точек , полученные по формулам (2) – (7), сходится к точке минимума.

Замечание. Формулы (2)-(7) не требовали гладкости функции 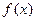. Однако в теореме это условие есть. Можно показать, что если функция не гладкая, то метод может не сходиться к точке минимума.

Дата добавления: 2015-01-03