Интерполяционные формулы Ньютона

Рассмотрим интерполяционный полином Ньютона с разделенными разностями (4.18), взяв в качестве узлов интерполирования равноотстоящие точки x₀, x₁ = x₀+ h, …,x_i=x₀+ih,…,x_n = x₀+nh. Заменяя разделенные разности их выражениями через конечные разности согласно (4.20)

,

получим

.

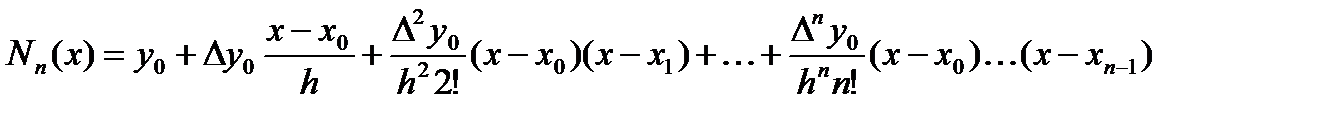Введем переменную 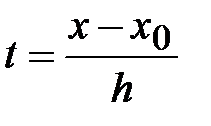. Тогда формула примет вид

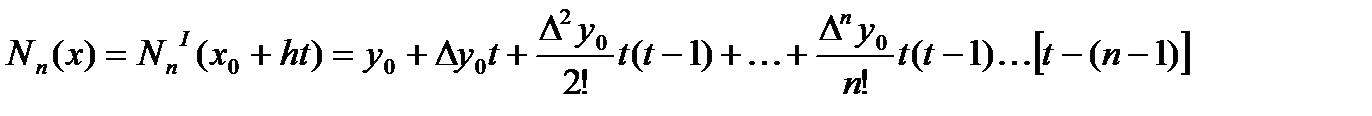. (4.22)

Полученную формулу называют первым интерполяционным полиномом Ньютона или полиномом Ньютона для интерполирования вперед.

Остаточная погрешность значения выражается формулой (4.8). Если заменить 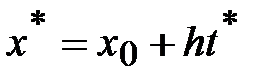, то она примет следующий вид:

.

На практике величина 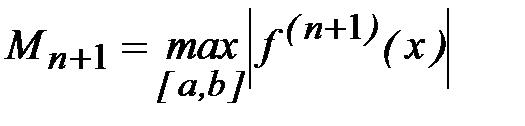оценивается согласно (4.21) с помощью конечных разностей (п+1)- го порядка

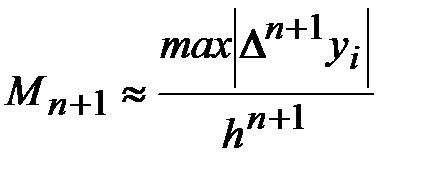
или 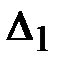определяется абсолютной величиной первого отброшенного слагаемого.

Введем еще одну интерполяционную формулу Ньютона. Для этого запишем полином Ньютона с разделенными разностями (4.18), присоединяя узлы в следующем порядке: :

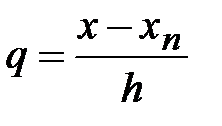Введем переменную . и выразим разделенные разности через конечные.

. (4.23)

Эта формула называется вторым интерполяционным полиномом Ньютона, или полиномом Ньютона для интерполирования назад.

Оценка (4.8) остаточной погрешности приближенного значения 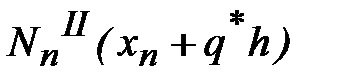представится в виде

.

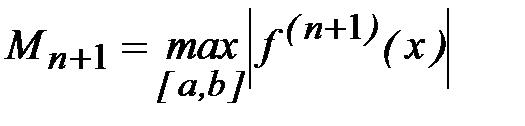Итак, получены две новые формулы интерполирования, и далее будут получен еще ряд таких формул. Однако следует заметить, что каждая из них является лишь другой формой записи интерполяционного полинома Лагранжа. Поэтому, если отвлечься от различия в обозначениях и в форме записи, то все эти формулы тождественны, когда они построены по одним и тем же узлам интерполирования. Однако в практике вычислений применяются в различных случаях разные формулы. Как уже отмечалось, во-первых, дело связано с тем, что обычно бывает удобнее вести вычисления, если при интерполировании сначала используются ближайшие к x^* узлы, а затем подключаются все более удаленные. При этом первые члены интерполяционных формул дадут основной вклад в искомую величину, а остальные будут давать лишь уменьшающиеся (по модулю) добавки. В этом случае легко установить, на какой разности следует закончить вычисления.

Во-вторых, как было отмечено в разделе 4.1, максимальные значения убывают к середине отрезка, содержащего все узлы, и возрастают к концам его. Поэтому, если имеется возможность при вычислениях для различных x строить интерполяционный полином по различным узлам, то их следует выбирать так, чтобы точка x находилась вблизи середины отрезка, содержащего все узлы интерполирования. В этом смысле мы можем сравнивать по точности различные интерполяционные формулы

Дата добавления: 2014-12-25