Интерполяционный полином Лагранжа

Будем строить интерполяционный полином в виде

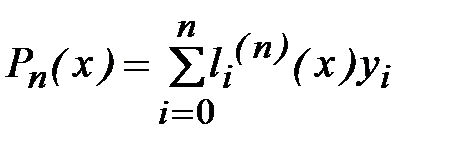, (4.9)

где 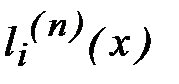– многочлены степени не выше п, обладающие следующим свойством:

.

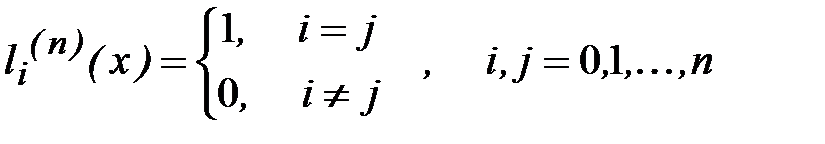Действительно, в этом случае полином (4.9) в каждом узле x_j, j=0,1,…n, равен соответствующему значению функции y_j, т.е. является интерполяционным.

Построим такие многочлены. Поскольку 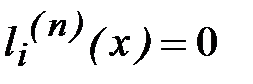при x=x₀,x₁,…x_i-1,x_i+1,…x_n, 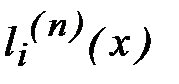можно следующим образом разложить на множители

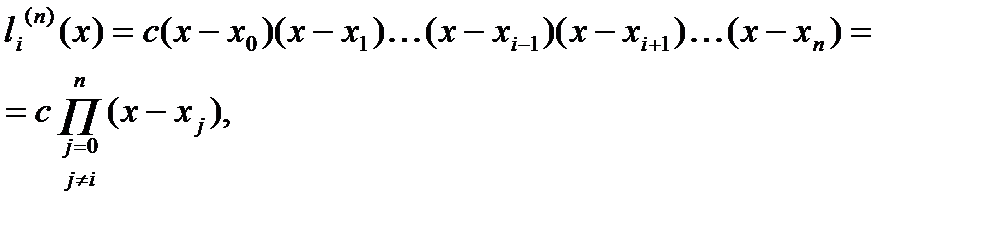
где с – постоянная. Из условия 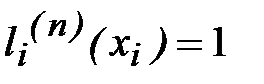получим, что

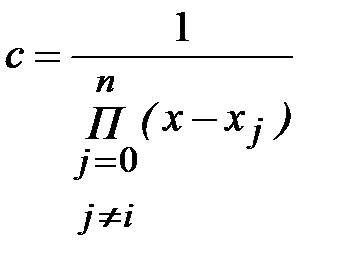и .

И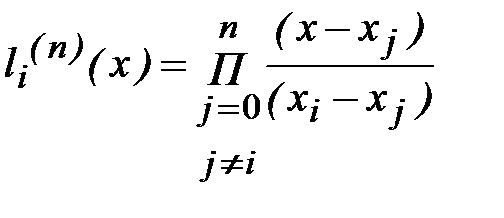нтерполяционный полином (4.1), записанный в форме

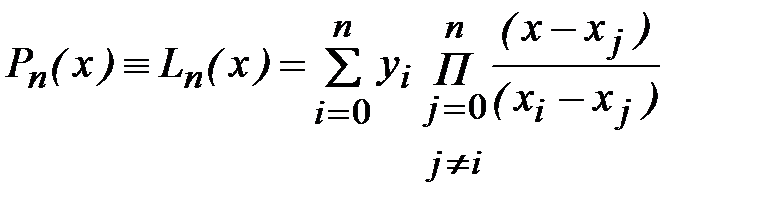, (4.10)

называют интерполяционным полиномом Лагранжа.

Приближенное значение функции в точке x^*, вычисленное с помощью полинома Лагранжа, будет иметь остаточную погрешность (4.8). Если значения функции y_i в узлах интерполирования x_i заданы приближенно с одинаковой абсолютной погрешностью , то вместо точного значения 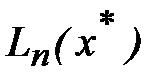будет вычислено приближенное значение 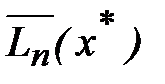, причем

,

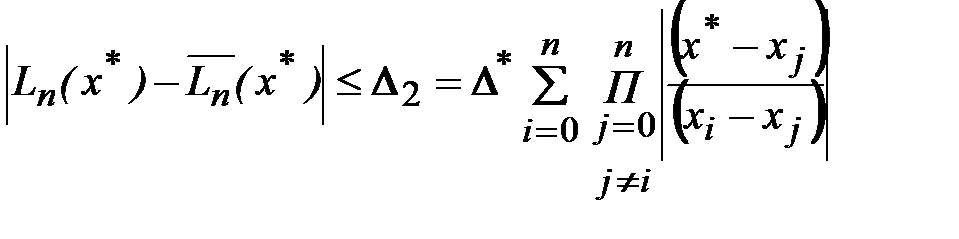где 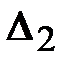– вычислительная абсолютная погрешность интерполяционного полинома Лагранжа. Окончательно имеем следующую оценку полной погрешности приближенного значения .

.

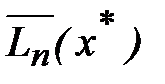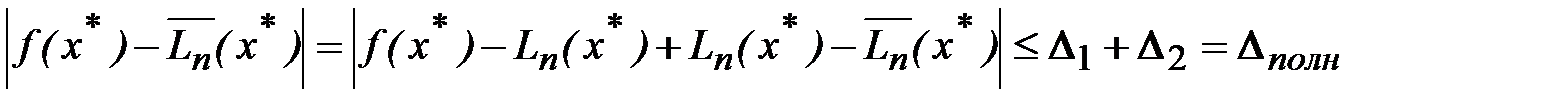В частности, полиномы Лагранжа первой и второй степени будут иметь вид

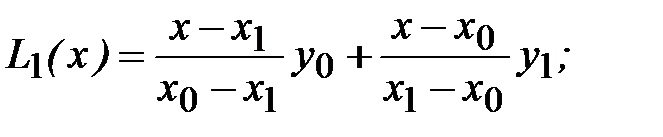
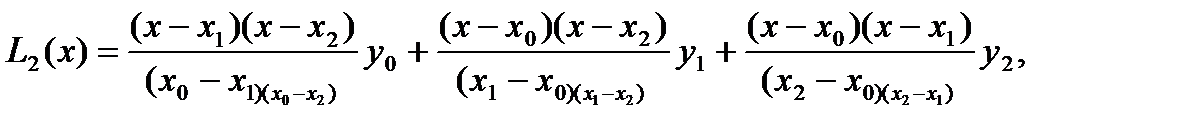
а их полные погрешности в точке x^*

,

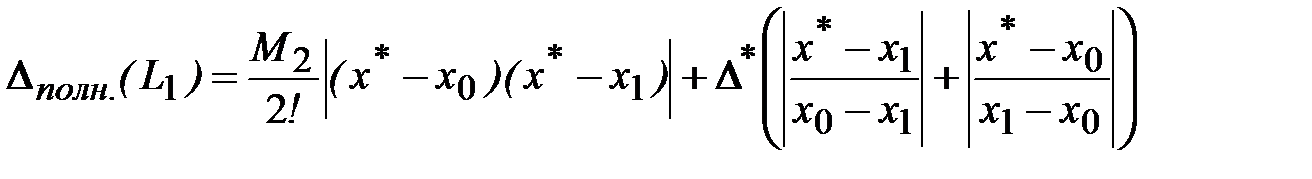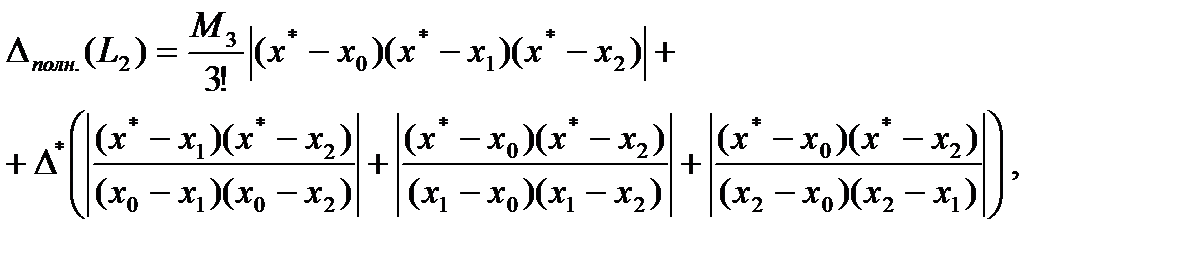
где ; .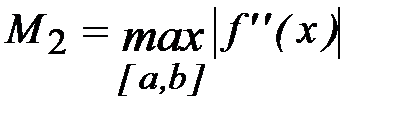

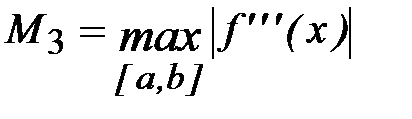
Существуют другие формы записи того же интерполяционного полинома (4.1), например, рассматриваемая далее интерполяционная формула Ньютона с разделенными разностями и ее варианты. При точных вычислениях значения Рn(х^*), получаемые по различным интерполяционным формулам, построенным по одним и тем же узлам, совпадают. Наличие же вычислительной погрешности приводит к различию получаемых по этим формулам значений. Запись многочлена в форме Лагранжа приводит, как правило, к меньшей вычислительной погрешности [1-3].

Использование формул для оценки погрешностей, возникающих при интерполировании, зависит от постановки задачи. Например, если известно количество узлов, а функция задана с достаточно большим количеством верных знаков, то можно поставить задачу вычисления f(x^*) с максимально возможной точностью. Если, наоборот, количество верных знаков небольшое, а количество узлов велико, то можно поставить задачу вычисления f(x^*) с точностью, которую допускает табличное значение функции, причем для решения этой задачи может потребоваться как разрежение, так и уплотнение таблицы.

§4.3. Разделенные разности и их свойства.

Понятие разделенной разности является обобщенным понятием производной. Пусть в точках x₀, x₁,…x_n заданы значения функций f(x₀), f(x₁),…,f(x_n). Разделенные разности первого порядка определяются равенствами

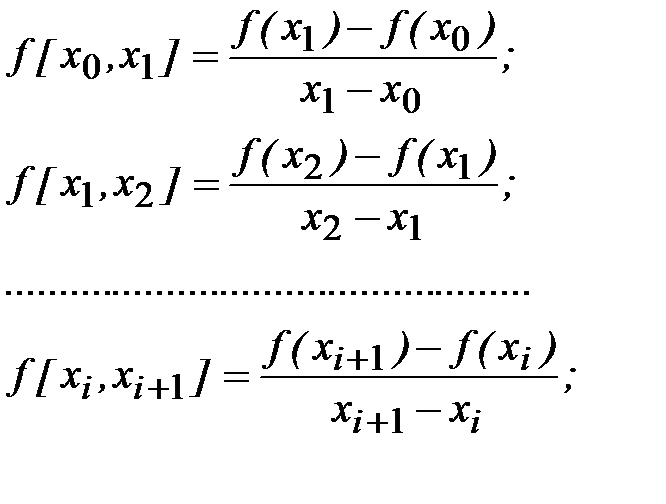
разделенные разности второго порядка – равенствами,

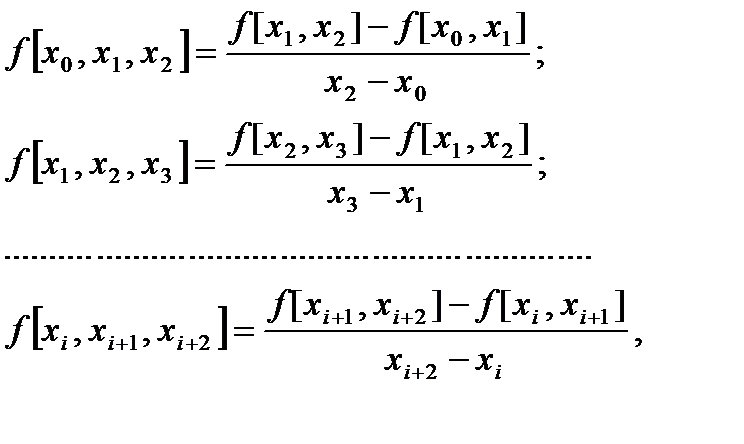
а разделенные разности k -го порядка определяются следующей рекуррентной формулой:

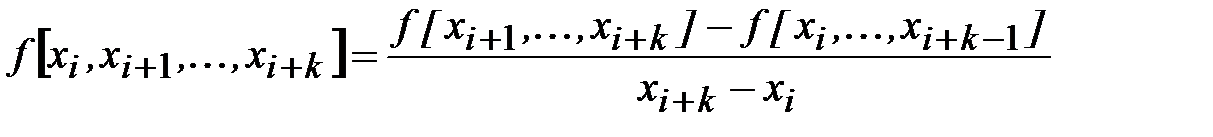(4.11)

Разделенные разности обычно помещаются в таблицу следующего вида:

хi	f(хi)	Разделенные разности
I порядка	II порядка	III порядка	IV порядка
х0	y0
		f[x0,x1]
х1	y1		f[x0,x1,x2]
		f [x1,x2]		f [x0,x1,x2,x3]
х2	y2		f [x1,x2,x3]		f[x0,x1,x2,x3,x4]
		f [x2,x3]		f [x1,x2,x3,x4]
х3	y3		f [x2,x3,x4]
		f [x3,x4]
х 4	y4

Рассмотрим следующие свойства разделенных разностей.

1. Разделенные разности всех порядков являются линейными комбинациями значений f(x_i), т.е. имеет место следующая формула:

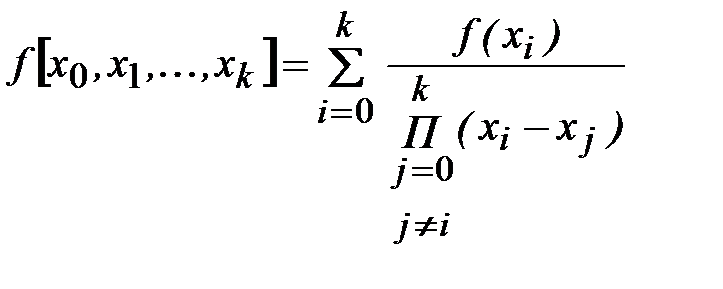. (4.12)

Докажем справедливость этой формулы индукцией по порядку разностей. Для разностей первого порядка

.

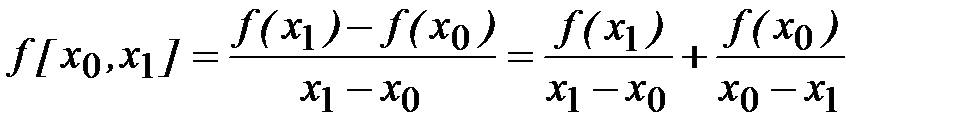Формула (4.12) справедлива. Предположим теперь, что она справедлива для всех разностей порядка .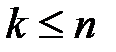

Тогда, согласно (4.11) и (4.12) для разностей порядка k=п+1 имеем

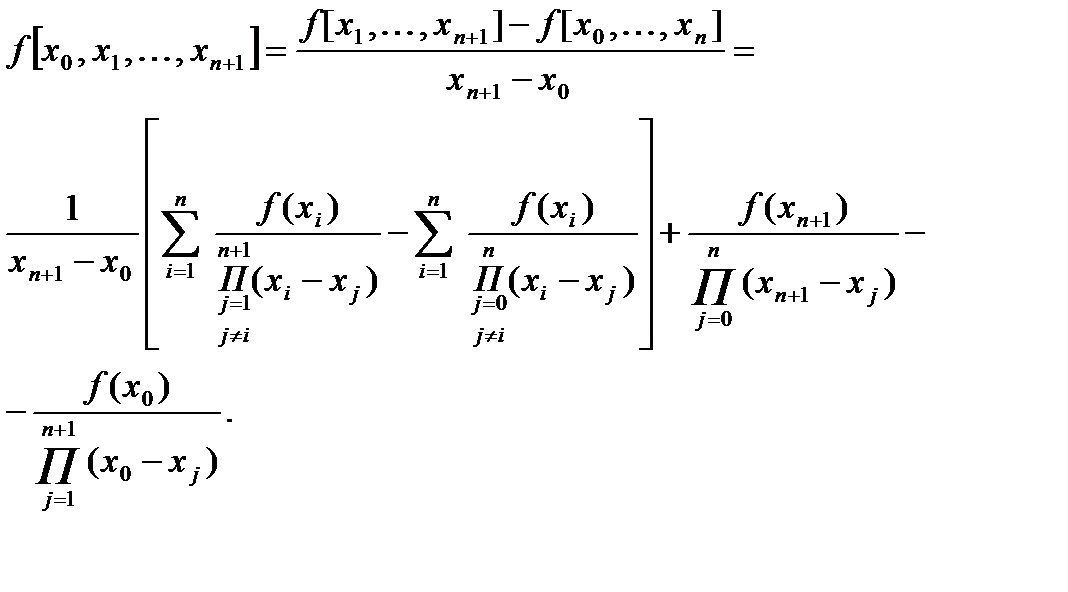
Слагаемые, содержащие f(x₀) и f(x_n+1), имеют требуемый вид. Рассмотрим слагаемые, содержащие f(x_i), i=1, 2, …,n. Таких слагаемых два - из первой и второй сумм:

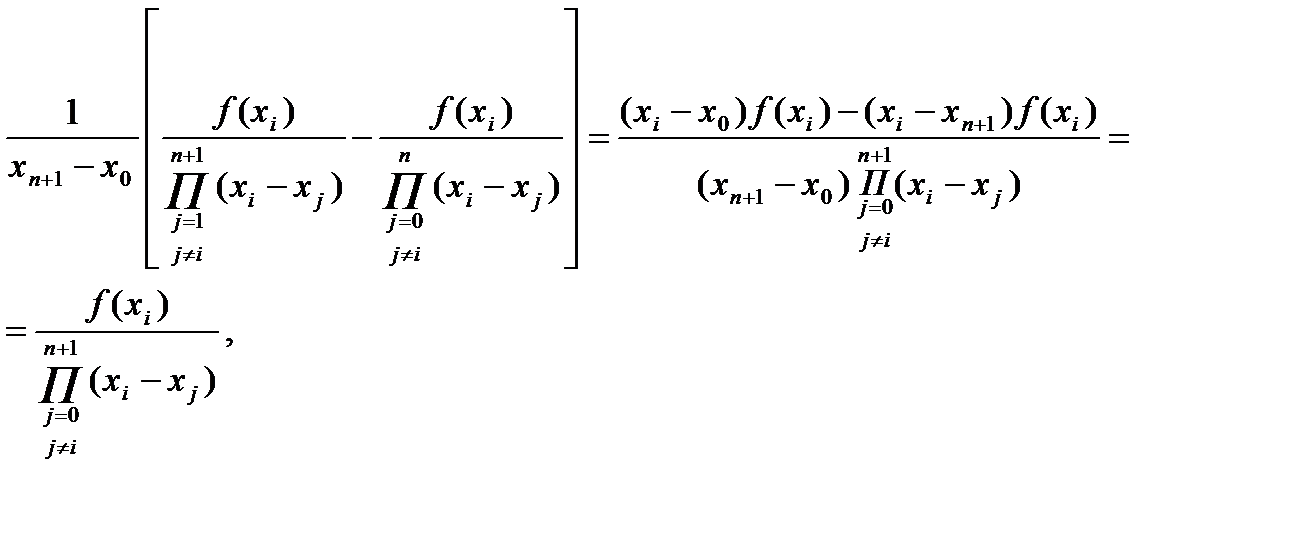
т.е. формула (4.12) справедлива для разности порядка k=п+1, доказательство закончено.

2. Разделенная разность есть симметрическая функция своих аргументов x₀, x₁,…x_n (т.е. не меняется при любой их перестановке):

.

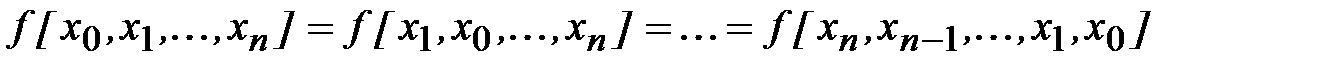Это свойство непосредственно следует из равенства (4.12).

3. Простую связь разделенной разности f[x₀, x₁,…,x_n] и производной f⁽ⁿ⁾ (x) дает следующая теорема.

Пусть узлы x₀, x₁,…x_n принадлежат отрезку [a, b] и функция f(x) имеет на этом отрезке непрерывную производную порядка п. Тогда существует такая точка xÎ[a, b], что

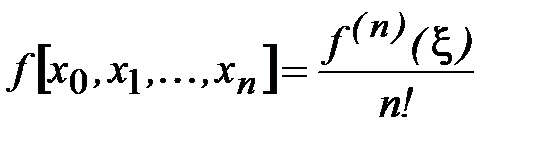. (4.13)

Докажем сначала справедливость соотношения

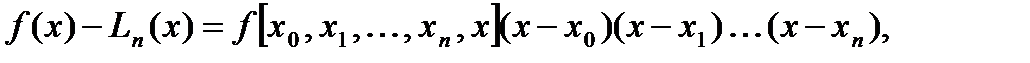(4.14)

где .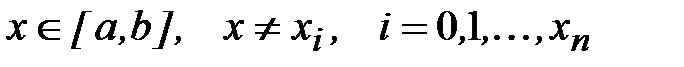

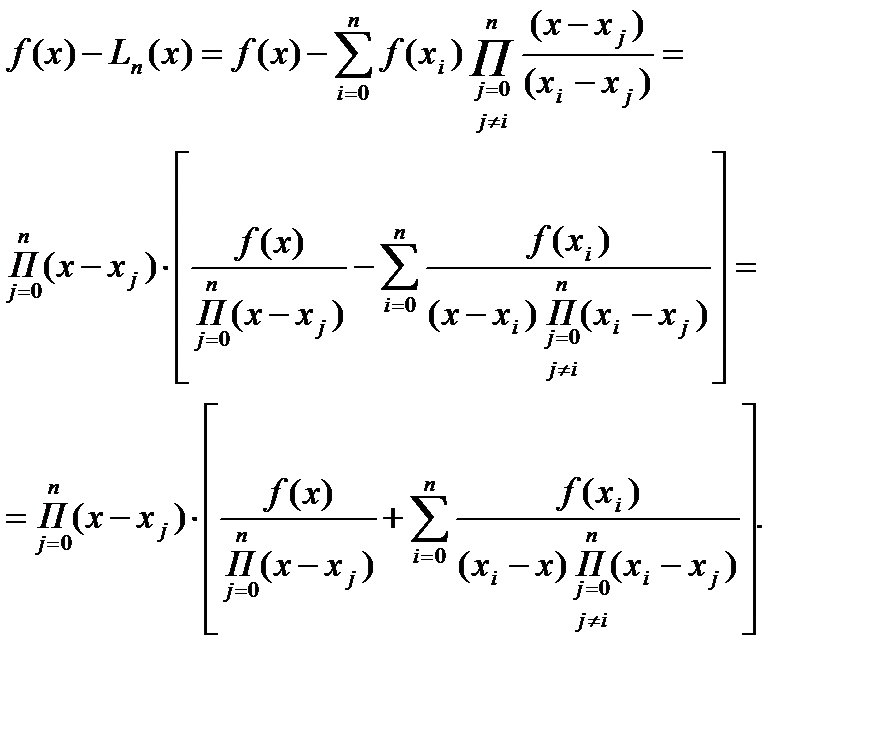
Согласно (4.12) выражение в квадратных скобках есть

f [x₀, x₁, …, x_n, x].

Из сравнения (4.14) с выражением (4.7) для остаточного члена R_n(x)=f(x)-L_n(x) получим (4.13), теорема доказана.

Из этой теоремы вытекает простое следствие. Для полинома п -ой степени

f(x) = a₀ xⁿ+a₁ x^n-1+…a_n

производная порядка п, очевидно, есть

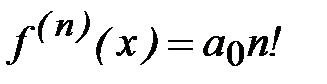
и соотношение (4.13) дает для разделенной разности значение

.

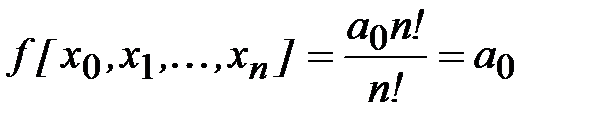Итак, у всякого многочлена степени п разделенные разности порядка п равны постоянной величине – коэффициенту при старшей степени многочлена. Разделенные разности высших порядков
(больше п), очевидно, равны нулю. Однако этот вывод справедлив лишь в случае отсутствия вычислительной погрешности у разделенных разностей.

§4.4. Интерполяционный полином Ньютона с разделенными разностями

Запишем интерполяционный полином Лагранжа в следующем виде:

(4.15)

где L₀(x) = f(x₀)=y₀, а L_k(x) – интерполяционный полином Лагранжа степени k, построенный по узлам x₀, x₁, …,x_k. Тогда 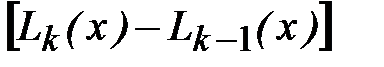есть полином степени k, корнями которого являются точки x₀, x₁, …,x_k-1. Следовательно, его можно разложить на множители

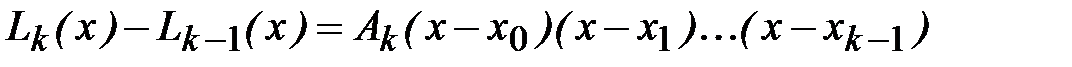(4.16)

где A_k – постоянная.

В соответствии с (4.14) получим

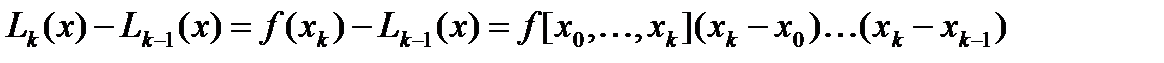(4.17)

Сравнивая (4.16) и (4.17) получим, что 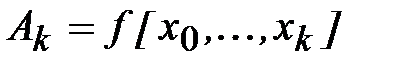и (4.15) примет вид

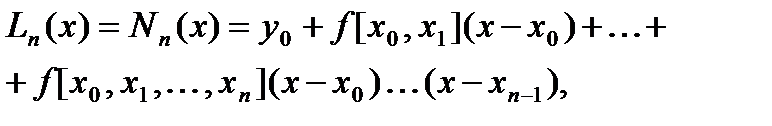(4.18)

который носит название интерполяционного полинома Ньютона с разделенными разностями.

Этот вид записи интерполяционного полинома более нагляден (добавлению одного узла соответствует появление одного слагаемого) и позволяет лучше проследить аналогию проводимых построений с основными построениями математического анализа.

Остаточная погрешность интерполяционного полинома Ньютона выражается формулой (4.8), но ее, с учетом (4.13), можно записать и в другой форме

,

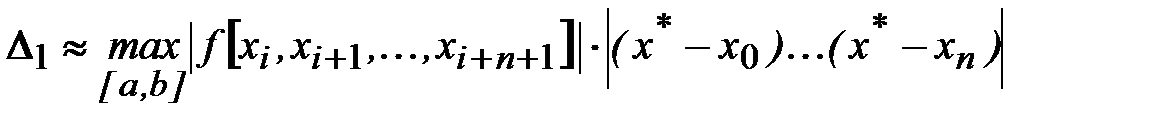т.е. остаточная погрешность может быть оценена модулем первого отброшенного слагаемого в полиноме N_n(x^*).

Вычислительная погрешность N_n(x^*) определится погрешностями разделенных разностей. Узлы интерполяции, лежащие ближе всего к интерполируемому значению x^*, окажут большее влияние на интерполяционный полином, лежащие дальше – меньшее. Поэтому целесообразно, если это возможно, за x₀ и x₁ взять ближайшие к x^* узлы интерполирования и произвести сначала линейную интерполяцию по этим узлам. Затем постепенно привлекать следующие узлы так, чтобы они возможно симметричнее располагались относительно x^*, пока очередной член по модулю не будет меньше абсолютной погрешности входящей в него разделенной разности.

Дата добавления: 2014-12-25