Графический метод решения задач линейного программирования (ЗЛП)

Общая задача оптимизации

В экономике оптимизационные задачи возникают в связи с многочисленностью возможных вариантов функционирования предприятия, при ситуациях выбора варианта, наилучшего по некоторому правилу или критерию, характеризуемому соответствующей целевой функцией (например, иметь минимум затрат, максимум продукции).

Отличительной особенностью оптимизационных моделей является наличие условия нахождения оптимального решения (критерия оптимальности), которое записывается в виде функционала. Эти модели при определенных исходных данных задачи позволяют получить множество решений, удовлетворяющих условиям задачи, и обеспечивают выбор оптимального решения, отвечающего критерию оптимальности.

В общем виде математическая постановка задачи математического программирования состоит в определении наибольшего или наименьшего значения целевой функции 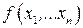при условиях

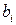, где и – заданные функции, а – некоторые действительные числа.

Задачи математического программирования делятся на задачи линейного и нелинейного программирования.

Если все функции и линейные, то соответствующая задача является задачей линейного программирования (ЗЛП), в противном случае перед нами задача нелинейного программирования (ЗНП).

В общем виде задача линейного программирования ставится следующим образом: найти вектор максимизирующий
линейную форму

и удовлетворяющий условиям

Линейная функция (4.1) называется целевой функцией задачи. Условия (4.2) называют функциональными, а (4.3) – прямыми ограничениями задачи.

Вектор , компоненты которого удовлетворяют условиям (4.2 – 4.3), будем называть планом или допустимым решением ЗПЛ.

Все допустимые решения образуют область определения ЗЛП или область допустимых решений (ОДР). Допустимое решение, максимизирующие целевую функцию (1), называют оптимальным планом задачи

где – оптимальное решение ЗЛП.

На практике хорошо себя зарекомендовали оптимизационные модели:

· определение оптимальной производственной программы;

· оптимального смешения компонентов;

· оптимального раскроя;

· оптимального размещения предприятия некоторой отрасли на определенной территории;

· формирования оптимального портфеля ценных бумаг;

· транспортной задачи.

Для решения ЗЛП применяется метод последовательно улучшения плана или симплекс-метод, который состоит из двух вычислительных процедур: симплекс-метода с естественным планом и симплекс-метода с искусственным планом (М-метод).

Выбор конкретной вычислительной процедуры осуществляется после приведения исходной задачи к каноническому виду (КЗПЛ):

Будем считать, что ЗПЛ записана в канонической форме, если ее целевая функция максимизируется, ограничения имеют вид равенств с неотрицательной правой частью и все переменные не отрицательные.

Графический метод решения ЗЛП является наиболее простым и применяется для решения задач ЛП с двумя переменными. Рассмотрим ЗЛП в стандартной форме:

Положим и будем рассматривать задачу на плоскости. Пусть система неравенств совместна (имеет хотя бы одно решение). Каждое неравенство этой системы графически определяет полуплоскость прямой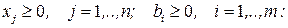

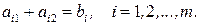
Условия не отрицательности определяют полуплоскости с граничными прямыми 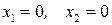соответственно.

Система совместна, поэтому полуплоскости, как выпуклые множества, пересекаясь, образуют общую часть, которая является выпуклым множеством и представляет собой совокупность точек, где координаты каждой точки являются решением данной системы. Совокупность этих точек называют многоугольником решений. Он может быть точкой, отрезком, лучом, ограниченным и неограниченным многоугольником.

Таким образом, геометрически решение ЗЛП представляет собой отыскание такой точки многоугольника решений, координаты которой доставляют линейной функции цели максимальное (минимальное) значение, причем допустимыми решениями являются все точки многоугольника решений.

Линейное уравнение описывает множество точек, лежащих на одной прямой. Линейное неравенство описывает некоторую область на плоскости.

Пример. Определить, какую часть плоскости описывает неравенство .

Дата добавления: 2014-12-26