Возможные ситуации графического решения ЗЛП

№	Вид ОДР	Вид оптимального решения
	Ограниченная	Единственное решение
Бесконечное множество решений
	Неограниченная	ЦФ не ограничена снизу
ЦФ не ограничена сверху
Единственное решение
Бесконечное множество решений
	Отрезок	Единственное решение
Бесконечное множество решений

4.3. Двойственность в ЗЛП. Анализ полученных
оптимальных решений

С каждой ЗПЛ тесно связана другая линейная задача, называемая двойственной задачей.

Первоначальная задача называется исходной или прямой. Связь исходной и двойственной задач заключается в том, что решение одной из них может быть получено непосредственно из решения другой.

Переменные двойственной задачи 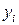называют объективно обусловленными оценками или двойственными оценками, или ценами ресурсов, или теневым ценами.

Каждая из задач двойственной пары фактически является самостоятельной ЗЛП и может быть решена независимо от другой задачи.

Двойственная задача по отношению к исходной задаче составляется согласно следующим правилам:

· ЦФ исходной задачи формулируется на максимум, а ЦФ двойственной задачи – на минимум, при этом в задаче на максимум все неравенства функциональных ограничений имеют вид 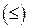, а в задаче на минимум – вид ;

· матрица 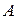, составленная из коэффициентов при неизвестных в системе ограничений исходной задачи, и аналогичная матрица 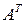в двойственной задачи получаются друг из друга транспонированием;

· число переменных в двойственной задаче равно числу функциональных ограничений исходной задачи, а число ограничений
двойственной задачи – числу переменных в исходной;

· коэффициентами при неизвестных в ЦФ двойственной задачи являются свободные переменные в системе ограничений исходной задачи, а правыми частями в ограничениях двойственной задачи – коэффициенты при неизвестных в ЦФ исходной;

· каждому ограничению одной задачи соответствует переменная другой задачи, номер переменной совпадает с номером ограничения. При этом ограничению, записанному в виде неравенства 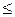, соответствует переменная, связанная условием не отрицательности. Если функциональное ограничение исходной задачи является равенством, то соответствующая переменная двойственной задачи может принимать как положительные, так и отрицательные значения.

Модель исходной (прямой) задачи в общем виде может быть записана следующем образом:

Модель двойственной задачи:

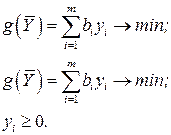
Две приведенные задачи образуют пару симметричных двойственных задач. Основные утверждения о взаимно двойственных задачах содержатся в следующих теоремах.

Первая теорема о двойственности. Для взаимно двойственных задач имеет место один из взаимоисключающих случаев:

1. В прямой и двойственных задачах имеются оптимальные решения при этом значения ЦФ на оптимальных решениях совпадают

2. В прямой задаче допустимое множество не пусто, а ЦФ на этом множестве не ограниченна сверху. При этом у двойственной задачи будет пустое допустимое множество.

3. В двойственной задаче допустимое множество не пусто, а ЦФ на этом множестве не ограниченна снизу. При этом у прямой задачи допустимое множество оказывается пустым.

4. Обе из рассматриваемых задач имеют пустые допустимые множества.

Вторая теорема двойственности (теорема о дополняющей
нежесткости). Пусть – допустимое решение прямой задачи, а 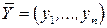– допустимое решение двойственной задачи. Для того чтобы они были оптимальными решениями соответственно прямой и двойственной задач, необходимо и достаточно, чтобы выполнялись следующие соотношения:

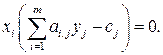
Условия (4.12) и (4.13) позволяют, зная оптимальное решение одной из взаимно двойственных задач, найти оптимальное решение другой задачи.

Рассмотрим еще одну теорему, выводы которой будем использовать в дальнейшем.

Теорема об оценках. Значения переменных 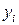в оптимальном решении двойственной задачи представляют собой оценки влияния свободных членов 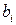системы ограничений (неравенств) прямой задачи на величину .

Решая ЗЛП симплекс-методом, мы одновременно решаем двойственную ЗЛП.

Переменные двойственной задачи 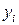называют объективно обусловленными оценками.

4.4. Специальные задачи линейного программирования.
Задачи целочисленного программирования

Под задачей целочисленного программирования (ЦП) понимается задача, в которой все или некоторые переменные должны принимать целые значения. В том случае, когда ограни­чения и целевая функция задачи представляют собой линейные зависимости, задачу называют целочисленной задачей линейного программирования. В противном случае, если хотя бы одна зави­симость – нелинейная, это будет целочисленная задача нелинейного программирования.

Особый интерес к задачам ЦП вызван тем, что во многих прак­тических задачах необходимо находить целочисленное решение ввиду дискретности ряда значений искомых переменных. К их числу относятся:

· задачи оптимизации раскроя;

· оптимальное проектирование машин и оборудования;

· оптимизация системы сервиса и технического обслуживания

машинно-тракторного парка и т.д.

Для нахождения оптимального решения целочисленных задач применяют специальные методы, в которых учитывается, что число возможных решений любой целочисленной задачи является конечным.

Задачи оптимизации, в результате решения которых искомые значения переменных должны быть целыми числами, называются
задачами (моделями) целочисленного (дискретного) программи­рования:

Если 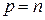, то задачу называют полностью целочисленной, если – частично целочисленной.

Существуют различные методы решения задач дискретного программирования (дискретной оптимизации). Наиболее часто используемым методом является метод ветвей и границ. Именно этот метод реализован в программе Поиск решения пакета Excel.

Дискретная оптимизация средствами Excel проводится анало­гично решению соответствующих непрерывных задач. Основное отличие заключается в том, что в диалоговом окне Поиск решения устанавливается требование целочисленности соответствующих переменных (при этом в режиме Параметры устанавливается тип задачи – линейная или нелинейная).

Дата добавления: 2014-12-26