Решение. 1. Неравенство преобразуем в равенство

1. Неравенство преобразуем в равенство. Строим прямую 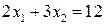. Она проходит через точки (6; 0) и (0; 4).

2. Для того чтобы определить, какая полуплоскость удовлетворяет неравенству, необходимо выбрать любую точку на графике, не принадлежащую прямой и подставить ее координаты в неравенство. Если неравенство будет выполняться, то данная точка является допустимым решением и полуплоскость, содержащая точку, удовлетворяет неравенству. Для постановки удобно использовать точку начала координат.

3. Подставим в неравенство . Получим . Данное утверждение является верным, следовательно, неравенству соответствует нижняя полуплоскость, содержащая точку (0; 0). Аналогично графически можно отобразить все ограничения ЗЛП.

4. Решением каждого неравенства системы ограничений ЗЛП является полуплоскость, содержащая граничную прямую и расположенную по одну сторону от нее. Пересечение полуплоскостей, каждая из которых определяется соответствующим неравенством системы, называется областью допустимых решений (ОДР) или областью определения .

Необходимо помнить, что ОДР удовлетворяет условиям не отрицательности .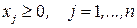

Координаты любой точки, принадлежащей области определения, являются допустимым решением задачи.

Для нахождения экстремального значения целевой функции при графическом решении ЗЛП используют вектор-градиент, координаты которого являются частными производными целевой функции:

Этот вектор показывает направление наискорейшего изменения целевой функции. Прямая , перпендикулярная вектору-градиенту, является линией уровня целевой функции.

В любой точке линии уровня целевая функция принимает одно и тоже значение. Приравниваем целевую функцию постоянной величине «a». Меняя значение «a» получим семейство параллельных прямых, каждая из которых является линией уровня целевой функции (ЦФ).

Важное свойство линии уровня ЦФ состоит в том, что при параллельном смещении линии в одну сторону уровень только возрастает, а при смещении в другую сторону уровень только убывает.

С геометрической точки зрения в ЗЛП ищется такая угловая точка или набор точек допустимого множества решений, на котором достигается самая верхняя (нижняя) линия уровня, расположенная дальше (ближе) остальных в направлении наискорейшего роста.

Графический метод решения ЗЛП состоит из следующих
этапов:

· строится многоугольная ОДР ЗЛП;

· строится вектор-градиент ЦФ в какой-нибудь точке , принадлежащей ОДР: ;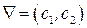

· линии уровня 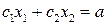(а – постоянная величина) – прямая, перпендикулярная вектору-градиенту 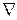, – передвигается в направлении этого вектора в случае максимизации 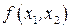до тех пор, по не покинет ОДР. Предельная точка (или точки) области при этом движении является точкой максимума ;

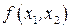· для нахождения координат точки максимума достаточно решить два уравнения прямых, получаемых из соответствующих ограничений и дающих в пересечении точку максимума. Значение 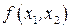, найденное в получаемой точке, является максимальным.

При минимизации (максимизации) функции 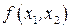линия уровня перемещается в направлении, противоположному вектору-градиенту. Если прямая, соответствующая линии уровня, при своем движении не покидает ОДР, то минимум (максимум) функции 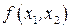не существует. Если линия уровня параллельна какому-либо ограничению задачи, то оптимальное значение ЦФ будет двигаться в любой точке этого ограничения, лежащей между двумя оптимальными угловыми точками, и соответственно, любая из этих точек является оптимальным решением задачи.

Возможные ситуации графического решения ЗЛП представлены в табл. 4.1.

Таблица 4.1

Дата добавления: 2014-12-26