Примеры вычисления. Пример 1. Вычислить ò dx/(x+2)

Пример 1. Вычислить ò dx/(x+2).

Решение. Обозначим t=x+2, тогда dx=dt, ò dx/(x+2) = ò dt/t = lnïtï+C =
= lnïx+2ï+C.

Пример 2. Найти ò tg x dx.

Решение. ò tg x dx = ò sin x/cos x dx = - ò d(cos x)/ cos x. Пусть t=cos x, тогда ò tg x dx = - ò dt/t = - lnïtï+C = - lnïcos xï+C.

Пример 3. Найти ò dx/sin x.

Решение.

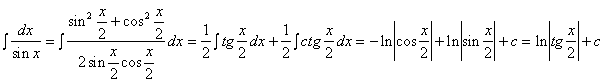
Пример 4. Найти .

Решение. =

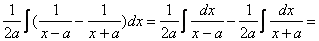
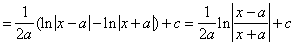
Пример 5. Найти ò arctg x dx.

Решение. Обозначим u=arctg x, dv=dx. Тогда du = dx/(x²+1), v=x, откуда ò arctg x dx = x arctg x - ò x dx/(x²+1) = x arctg x + 1/2 ln(x²+1) +C; так как
ò x dx/(x²+1) = 1/2 ò d(x²+1)/(x²+1) = 1/2 ln(x²+1) +C.

Пример 6. Вычислить ò ln x dx.

Решение. Применяя формулу интегрирования по частям, получим:
u=ln x, dv=dx, du= 1/x dx, v=x. Тогда ò ln x dx = x lnx - ò x 1/x dx =
= x lnx - ò dx = x lnx - x + C.

Пример 7. Вычислить ò e^x sin x dx.

Решение. Обозначим u = e^x, dv = sin x dx, тогда du = e^x dx, v=ò sin x dx= - cos x Þ ò e^x sin x dx = - e^x cos x + ò e^x cos x dx. Интеграл ò e^x cos x dx также интегрируем по частям: u = e^x, dv = cos x dx Þ du=e^xdx, v=sin x. Имеем:
ò e^x cos x dx = e^x sin x - ò e^x sin x dx. Получили соотношение ò e^x sin x dx = - e^x cos x + e^x sin x - ò e^x sin x dx, откуда 2 ò e^x sin x dx = - e^x cos x + e^x sin x + С.

Пример 8. Вычислить J = ò cos(ln x)dx/x.

Решение. Так как dx/x = d(ln x), то J= ò cos(ln x)d(ln x). Заменяя ln x через t, приходим к табличному интегралу J = ò cos t dt = sin t + C = sin(ln x) + C.

Пример 9. Вычислить J = .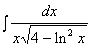

Решение. Учитывая, что = d(ln x), производим подстановку ln x = t. Тогда J = .

Пример 10. Вычислить интеграл J = .

Решение. Имеем: . Поэтому =
=
= .

Задание для практической работы по теме «Применение формулы Ньютона-Лейбница, свойств определенного интеграла при вычислениях. Методы интегрирования по частям и подстановкой».

Вариант 1	Вариант 2
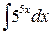Найти интегралы a) b) c)	Найти интегралы a) 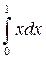b) c)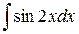
Вариант 3	Вариант 4
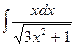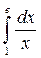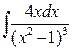Найти интегралы a) b) c)	Найти интегралы a) b) c)
Вариант 5	Вариант 6
Найти интегралы a) b) c)	Найти интегралы a) 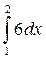b) c)
Вариант 7	Вариант 8
Найти интегралы a) b) c)	Найти интегралы a) b) c)

Практическая работа № 7.

Тема 1.7: «Геометрический смысл определенного интеграла. Вычисление площади плоской фигуры с помощью определенного интеграла»

Цель: Применять формулу Ньютона-Лейбница для вычисление площади плоской фигур.

Теоретический материал :

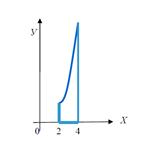
Геометрическая интерпретация: определенный интеграл представляет собой площадь криволинейной трапеции, ограниченной сверху кривой y= f(x), прямыми x = a и x = b и отрезком оси Ox.

Задание для практической работы по теме «Геометрический смысл определенного интеграла. Вычисление площади плоской фигуры с помощью определенного интеграла»

Вариант 1	Вариант 2
Вычислить площадь фигуры, ограниченной линиями:   1. y=x^2-2x-3; x=3; x=4; y=0.   2. Y=x^2+4x+5, y=5 3. Y=sinx, y= .	Вычислить площадь фигуры, ограниченной линиями:   1. y=x^2+5x+4; x=-1; x=0; y=0.   2. Y=x^2+4x+4, y=1.   3. Y=ctgx, y=tgx,y=0 на отрезке .
Вариант 3	Вариант 4
Вычислить площадь фигуры, ограниченной линиями:   1. y=x^2-4x+3; x=3; x=5; y=0.   2. Y=x^2-4x, y=x.   3. Y= , x=2,x=4,y=0.	Вычислить площадь фигуры, ограниченной линиями:   1. y=x^2+2x-3; x=1; x=2; y=0.   2. Y=x^2, y=x-2.   3. х^2+y^2=16,y=2, y= .
Вариант 5	Вариант 6
Вычислить площадь фигуры, ограниченной линиями:   1. y=x^2-4; x=2; x=3; y=0.   2. Y=-x^2+x+6, y=-2x+6.   ^3.Y=x^2-4x+4,y=4-x^2	Вычислить площадь фигуры, ограниченной линиями:   1. y=x^2-x-2; x=2; x=3; y=0.   2. Y=-x^2+5x-4, y=2.   3. Y=x^3, 3x+2y-6=0,y=0

Практическое занятие №8

Тема 1.8:" Решение дифференциальных уравнений с разделяющимися переменными первого порядка "

Цель: Решать дифференциальные уравнения с разделяющимися переменными первого порядка.

Теоретический материал :

Дифференциальным уравнением (ДУ) называется такое уравнение, которое содержит производные или дифференциалы от искомой функции, а также может содержать саму искомую функцию и независимые переменные. ДУ называется обыкновенным, если искомая функция зависит только от одной переменной. Говорят, что ДУ имеет порядок n, если в него входят производные (дифференциалы) порядка n и не входят производные (дифференциалы) высших порядков. Общим решением ДУ порядка n называется функция y = y (x, c ₁ ,..., c_n) от независимой переменной x с n параметрами (константами) c ₁ ,..., c_n такая, что при любых фиксированных значениях параметров эта функция при подстановке в уравнение обращает последнее в тождество. Задачей Коши называется задача нахождения таких фиксированных значений констант, что в результате искомая функция будет удовлетворять начальным условиям y (x ₀) = y ₀, y' (x ₁) = y ₁ ,..., Такая функция с фиксированными значениями констант называется частным решением ДУ. ДУ возникают в исследованиях в различных областях человеческой деятельности: в физике, технике, экономике, — практически везде, где применяется дифференциальное исчисление.

Уравнение (1)

где функции f (x), g (y) непрерывны при рассматриваемых значениях x и y, называется ДУ с разделяющимися переменными.

Алгоритм решения.

1. Уравнение (1) может быть записано в виде (2)

Случай, когда функция g (y) = 0 привел бы нас к уравнению y' = 0, решением которого является y = C.

2. Интегрируем обе части уравнения (2):

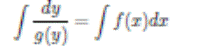
получаем общее решение y уравнения (1) (возможно в виде неявной функции).

3. Если дана задача Коши, подставляем начальные условия в формулу общего решения и находим соответствующее частное решение.

Дата добавления: 2014-12-26