Метод Гаусса

Формулы Крамера.

Матричный метод.

Методы решения общих систем линейных уравнений.

Запишем систему (1) в матричном виде:
AX=B, где

Рассмотрим случай, когда число неизвестных совпадает с числом уравнений.
Тогда решение системы находится по формуле:

A^-1B=X

Составим матрицу A*, элементами которой являются алгебраические дополнения матрицы A:

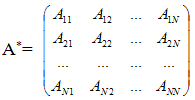
транспонируем ее и каждый элемент разделим на det A, получим матрицу

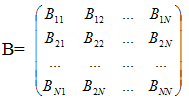, где B_ij=A_ij/det A, i=1,..,n; j=1,..,n.

Матрица B=A^-1. Тогда решение системы (1) можно найти по формулам

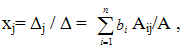j=1,..,n.
Эти формулы называются формулами Крамера.

Метод Крамера и матричный метод применимы, если СЛУ имеет единственное решение.

Рассмотрим систему m линейных уравнений с n неизвестными

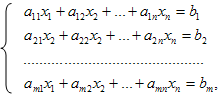i=1,…..,m; j=1,…..,n, (1)

Пусть . Разделим все члены первого уравнения на :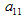

(2)
где
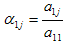(j =1,2…n + 1), (3)

Рассмотрим i-е уравнение системы(1):

(4)

Для исключения из этого уравнения х₁ умножим уравнение (2) на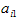
и полученное уравнение вычтем из уравнения (4). Тогда будем иметь

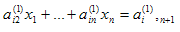(5)

где (6)

Таким образом, получаем укороченную систему

(7)

коэффициенты которой определяют по формулам (6).

Если ее ведущий коэффициент , то из системы (7) указанным выше приемом можно исключить неизвестное х₂, причем новые коэффициенты будут вычисляться по формулам типа (6) и т.д. Эта часть вычислений называется прямым ходом метода Гаусса.

Для определения неизвестных х₁,х₂,...х_n рассмотрим уравнения

(8)

Отсюда последовательно находим неизвестные (обратный ход):

(9)

Заметим,что операции (9)выполняются без деления.
Если очередной ведущий коэффициент окажется равным нулю, то уравнения системы следует переставить надлежащим образом. Возможно, конечно, что система (1) несовместна. Тогда, естественно, метод Гаусса не допускает реализации.

Дата добавления: 2015-04-24