Простые методы оценки инвестиций 5 страница

[править]Простейший поток

Однородный стационарный поток без последействий является простейшим, потоком Пуассона.

Число событий такого потока, выпадающих на интервал , распределено по Закону Пуассона:

Пуассоновский поток заявок удобен при решении задач ТМО. Строго говоря простейшие потоки редки на практике, однако многие моделируемые потоки допустимо рассматривать как простейшие.

[править]Мгновенная плотность

Мгновенная плотность (интенсивность) потока равна пределу отношения среднего числа событий, приходящихся на элементарный интервал времени (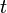, 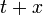) к длине интервала (), когда последний стремится к нулю.

или, для простейшего потока,

где равно математическому ожиданию числа событий на интервале .

[править]Формула Литтла

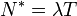
Среднее число заявок в системе равно произведению интенсивности входного потока на среднее время пребывания заявки в системе.

56. Матричные методы анализа.

матричный анализ — метод исследования взаимосвязей между экономическими объектами с помощью их матричного моделирования. * * * МАТРИЧНЫЙ АНАЛИЗ МАТРИЧНЫЙ АНАЛИЗ, метод исследования взаимосвязей между экономическими объектами с помощью их матричного моделирования

Матричные методы анализа, основанные на линейной и векторноматричной алгебре, применяются для изучения сложных и высокоразмерных структур как на отраслевом уровне, так и на уровне предприятий и их объединений.

Применение матричных методов покажем на следующем примере.

Два цеха предприятия выпускают продукцию двух видов: первый цех — продукцию 1-го вида, второй цех — продукцию 2-го вида. Часть выпускаемой продукции идет на внутреннее потребление, остальная является конечным продуктом. Требуется выявить распределение между цехами продукции, идущей на внутреннее потребление (xij), и общие (валовые) объемы выпускаемой продукции (л:),если заданы параметры прямых затрат (А) и конечного продукта (у

Элементы матрицы прямых затрат А представляют собой коэффициенты прямых затрат продукции /-го вида на производство единицы продукции /-го вида. В нашем примере эти коэффициенты будут такими:

Элементы векторстолбца у определяют величину конечного продукта, идущего на внешнюю реализацию:

н;;)=РДля определения валового (общего) выпуска продукции 1-го и 2-го видов воспользуемся следующей формулой:

х = (Е—А)-*у,

где Е — единичная матрица; (ЕА)"

матрица полных затрат;

(ЕА) =

Определитель этой матрицы равен:

ГГ-(-10-Н-4-) 16 1

25~40~

Получим обратную матрицу В = (Е—А) методом алгебраических дополнений.

Матрица алгебраических дополнений D формируется следующим образом:

,=(-1) у =у, d = ()=-;

V d I d'

57. Теория нечетких множеств.

Теория нечётких множеств (Заде) — это расширение классической теории множеств, используется в нечёткой логике. Впервые предложена Лотфи А. Заде в 60-х годах XX века.

В классической теории множеств принадлежность элементов множеству оценивается в бинарных терминах в соответствии с чётким условием — элемент либо принадлежит, либо нет данному множеству. Напротив, теория нечётких множеств разрешает градуированную оценку отношения принадлежности элементов множеству; то есть это отношение описывается при помощи функции принадлежности . Нечёткие множества — это расширение классической теории множеств, поскольку на некотором множестве функция принадлежности может действовать так же, как индикаторная функция, отображая все элементы либо в 1, либо в 0, как в классическом варианте.

[править]Определение

Нечёткое множество на классическом множестве определяется как следующее:

Функция принадлежности количественно градуирует принадлежность элементов фундаментальному множеству . Отображение элемента в значение 0 означает, что элемент не принадлежит данному множеству, значение 1 описывает полной принадлежности элемента множеству. Значения, лежащие строго между 0 и 1, характеризуют «нечёткие» элементы.

Нечёткое множество и чёткое (crisp) классическое множество

Следующие соотношения выполнены для значений функции принадлежности

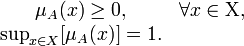
[править]Применения

Нечёткое множество B, где B = {(3,0.3), (4,0.7), (5,1), (6,0.4)} в стандартных обозначениях теории нечётких множеств обычно записывается как B = {0.3/3, 0.7/4, 1/5, 0.4/6}. Заметим, что произвольное значение со степенью принадлежности нуль zero не появляется в этом выражении нечёткого множества. Стандартное обозначение для степени принадлежности нечёткому множеству B значения 6 выглядит так: μB(6) = 0.4.

[править]Нечёткая логика

В качестве расширения многозначной логики оценками (valuations) () пропозициональных переменных () на множестве степеней принадлежности () может рассматриваться функция принадлежности, отображающая предикаты в нечёткое множество (или более строго, в упорядоченное множество нечётких пар, называемых нечётким отношением). Такими оценками (valuations) многозначная логика может быть расширена до того, чтобы разрешить нечёткие подстановки, из которых могут быть сделаны градуированные выводы.

Иногда это расширение называют «нечёткой логикой в узком смысле» в противопоставление «нечёткой логике в широком смысле», которая возникла в прикладных областях автоматического управления и инженерии знаний, и которая охватывает много тем, включающих нечёткие множества и «приближенные рассуждения».

Промышленные применения нечётких множеств в контексте «нечёткой логики в широком смысле» можно найти в нечёткой логике.

[править]Нечёткое число

Нечёткое число — это выпуклое, нормализованное нечёткое множество , чья функция принадлежности по крайней мере кусочно непрерывна и имеет функциональное значение 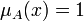на точно одном элементе. Это можно связать с игрой в пари «предположите ваш вес», где некто предполагает вес соперников, и чем ближе предположения, тем они правильнее, а «побеждает» тот, чьи предположение веса соперников ближе остальных (будучи полностью правильным, когда функцией принадлежности равна 1).

[править]Нечёткий интервал

Нечёткий интервал — это неопределенное множество со средним интервалом, чьи элементы обладают функцией принадлежности 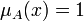. Как и для нечётких чисел, функция принадлежности должна быть выпуклой, нормализованной и по крайней мере кусочно непрерывной.

58. Способы сравнения в анализе хозяйственной деятельности.

Дата добавления: 2015-04-24