
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Біфуркації періодичних рухів. Каскад Фейгенбаума
|
|
|
|
Одним з найбільш практично важливих результатів теорії біфуркацій є встановлення факту наявності закономірностей у чергуванні біфуркацій при зміні параметрів системи в ході її еволюції. Більше того, множина сценаріїв такого чергування, на щастя, виявилась доволі обмеженою. Зокрема, у природі часто реалізується сценарій багатократного подвоєння періоду (частоти) коливань у системі. Механізми цього процесу пояснимо на прикладі динамічної системи Дуффінга, яка моделює осциляції багатьох природних систем (напр. вимушені коливання твердого тіла на пружині зі змінною жорсткістю, осциляції в електричних колах, тощо). Рівняння Дуффінга у загальному випадку має вигляд:
ẍ + εẋ + kx + βx3 = Fcos(ωt)
У фазовому просторі (ẋ, x)за, наприклад, наступного вибору параметрів ε=1, k=1, β=15.5, F=50, ω=3 атрактором системи є граничний цикл, який зображено на рисунку 1:
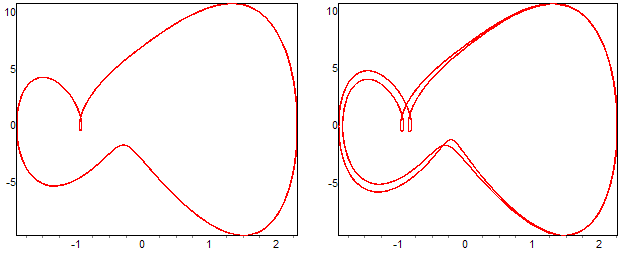
Біфуркація подвоєння періоду в системі Дуффінга.
При β = 15.6(рис. 2) внаслідок біфуркації траекторія граничного циклу ділиться на два подібні півцикли, через що загальний період коливань подвоюється. За подальшого збільшення параметра β (до 22.3 і далі) цей період зростає удвічі з кожною новою біфуркацією. При достатньо великих β ~ 30 атрактор системи надзвичайно ускладнюється наближаючись до хаотичного режиму дивного.
|
|
|
|
|
Дата добавления: 2015-05-08; Просмотров: 871; Нарушение авторских прав?; Мы поможем в написании вашей работы!