
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Числові методи розв’язування систем лінійних рівнянь
|
|
|
|
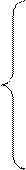 a11x1 + a12x2 + …+ a1nxn = b1
a11x1 + a12x2 + …+ a1nxn = b1
a21x1 + a22x2 + …+ a2nxn = b2
.
. Þ 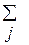 aijxj= bi (i = 1,n)
aijxj= bi (i = 1,n)
.
an1x1 + an2x2 + …+ annxn = bn
Число елементарних операцій при розв’язуванні лінійних систем з n-змінними пропорційно ~ n3.
Нехай система має єдиний розв’язок і число невідомих співпадає з кількістю рівнянь. За способом організації обчислень методи розв’язку систем лінійних рівнянь можна розділити на прямі та ітераційні.
Прямі методи дозволяють отримати розв’язок системи у вигляді точних формул після виконання скінченого числа арифметичних операцій над коефіцієнтами системи і вільними членами. Це метод Гауса і правило Крамера.
Ітераційні методи дозволяють отримати розв’язок системи з заданою точністю шляхом нескінченно збіжних процесів. Із наближених методів розглянемо метод ітерацій.
За способом організації обчислень методи розв’язку систем лінійних рівнянь можна розділити на прямі та ітераційні.
Прямі методи дозволяють знайти розв’язок у вигляді точних формул. Термін,,точний’’ є характеристикою алгоритму обчислень, а не реального обчислювального процесу. Абсолютно точний результат неможливий через обмеженість розрядної сітки. Прямі методи мають переваги: заздалегідь відома точна кількість операцій, які потрібно виконати. Вони універсальні, але разом з тим мають недоліки:
- Вимагають збереження в ОП всіх елементів матриці А, навіть, якщо серед них є багато нульових.
- При розрахунках відбувається накопичення похибок, так як результат наступного кроку обчислень використовує результат попереднього.
- При застосуванні прямих методів доцільно розв’язувати системи з густо заповненою матрицею. Тому широко використовують ітераційні методи. В них задається початкове значення невідомих: x1(0), x2(0),…,xn(0) і врезультаті ітераційних циклів отримуються наступні наближення. Вважається, що розв’язок знайдений з точністю e, якщо виконується умова êxi(n)-xi(n-1) |< e (i=1,2,…,n).
|
|
|
Переваги:
- Ітераційні методи не завжди вимагають збереження всієї матриці. Потрібні коефіцієнти можна знаходити в процесі розрахунку.
- Вони не накопичують похибок так як результат на n-ітерації не залежить від попередніх разів.
- Вони годяться для широкого класу систем і погано обумовлених систем.
Вибір методу розв’язку систем лінійних рівнянь залежить від кількох факторів:
1.Від особливостей матриці А
2.Від розмірності А
3.Від характеристик комп’ютера: його швидкодії, ОП,
зовнішніх носіїв.
A×X=B
Матриця коефіцієнтів називається неособливою або не виродженою, якщо існує обернена до неї матриця А-1×А= А×А-1= І.
 |
 a11 a12... a1n
a11 a12... a1n
.
A =.
.
an1 an2 ... ann
X =  B =
B = 
 a11 0 0 0
a11 0 0 0
0 a22 0 0
0 0 a33 0 - діагональна квадратна
0 0 0 ann
 |
1 0 0 0
0 1 0 0 - одинична, нульова
0 0 1 0
0 0 0 1
Якщо застосовувати до систем лінійних рівнянь елементарні перетворення, то отримаємо рівносильні системи, тобто системи, що мають такий же розв’язок. Елементарні перетворення:
1. множення всіх елементів рядка на одне і те ж число, яке ¹ 0.
2. додавання до елементів одного рядка відповідних елементів іншого рядка, помножених на загальне для всіх число.
3. перестановка рядків або стовпців.
Метод послідовного виключення змінних (Гауса)
 Він оснований якраз на елементарних перетвореннях. Схема – квадратна матриця перетворюється в трикутну. Розберем схему єдиного ділення.
Він оснований якраз на елементарних перетвореннях. Схема – квадратна матриця перетворюється в трикутну. Розберем схему єдиного ділення.
a11х1 + а12х2 + а13х3 = b1
a21х1 + а22х2 + а23х3 = b2
a31х1 + а32х2 + а33х3 = b3
Нехай а11¹ 0
Розділимо коефіцієнти першого рівняння і вільний член на а11. Отримаємо а 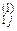 =
=  і b
і b 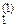 =
=  (1)
(1)
x1 + a 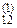 x2 + a
x2 + a 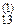 x3 = b
x3 = b 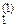 (2)
(2)
Тепер виключимо змінну х2 з другого і третього рівнянь. Для цього від другого рівняння віднімемо перше, помножене на а21, а від третього - помножене на а31. Отримаємо
|
|
|
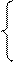 a
a  x2 + a
x2 + a 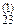 x3 = b
x3 = b  (3)
(3)
a 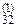 x2 + a
x2 + a  x3 = b
x3 = b 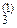 , де (4)
, де (4)
a  = аij - a
= аij - a 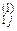 ai1 (i = 2,3; j = 2,3)
ai1 (i = 2,3; j = 2,3)
b 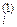 = bi - a
= bi - a 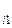 b
b 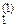
Далі (3) ділимо на а  Þ
Þ
x2 + a 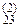 x3 = b
x3 = b  і виключимо х2 із (4).
і виключимо х2 із (4).
Отримаємо х3 = 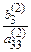
Якщо х1, х2, х3 підставити в початкову систему, то повинні отримати тотожність, але в зв’язку з тим, що проводились заокруглення чисел, то в результаті підстановки отримаємо деякі числа, відмінні від нуля. Ці числа називають нев’язками. Якщо нев’язки малі, то рішення є вірним.
Алгоритм
А×Х = В
 Введемо розширену матрицю
Введемо розширену матрицю
 a11 a12... a1n b1
a11 a12... a1n b1
a21 a22... a2n b2
.
(А|B) =.
an1 an2... ann bn
A(N,N); B (N)
Розв’язок X(N) розмістимо в В.
1) Ділимо перший рядок (А|B) на а11, потім множимо його послідовно на ак1 (k =2...n) і віднімаємо його від k-ого рядка. Після цього отримаємо наступну матрицю:
2)  1 a
1 a 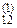 ... a
... a 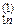 b
b 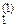
0 a  ... a
... a 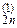 b
b 
.
.
.
0 a 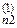 ... a
... a  b
b 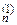
3) Елементи другого рядка ділимо на а  , потім множимо на а
, потім множимо на а 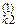 (k = 3…n) і віднімаємо від k-ого рядка.
(k = 3…n) і віднімаємо від k-ого рядка.
4)  Продовжуємо цей процес до тих пір, поки ця процедура не повториться (n-1) раз. Тоді отримаємо:
Продовжуємо цей процес до тих пір, поки ця процедура не повториться (n-1) раз. Тоді отримаємо:
1 a 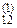 ... a
... a 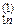 b
b 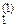
0 1 a 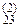 ... a
... a 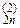 b
b 
0 0 1... a 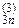 b
b 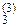
.
.
.
0 0 0... 1 a  b
b 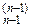
0 0 0 … 0 1 b 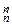
На цьому прямий хід методу Гауса закінчується.
5) Виконуємо обернений хід метода Гауса. В (n-1) рядок підставляємо значення хn і знаходимо хn-1 і т.д. за формулами
Правилом Крамера вже для n=4 не користуються, бо число операцій:
N (n) = (n2-1) n! +n, а для Гауса
N (n) = 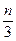 (n2+3n - 1)
(n2+3n - 1)
| Тобто при: n = 5 n=10 | По Крамеру N = 2885 N = 360∙106 | По Гаусу N = 65 N = 430 |
Метод Гауса – в теорії числових методів показується, що при виконанні прямого ходу методу Гауса треба виконати n3/2 – додавань, ~ n3/3 – множень, ~ n2/2 – ділень. На оберненому ході методу Гауса ~n2/2 – додавань, ~ n2/2 – множень, ~ n – ділень. Отже, приведення матриці до трикутного вигляду на порядок складніше ніж знаходження невідомих.
При розробці алгоритму обов’язково треба перевірити а11≠0. Якщо а11=0, тоді серед коефіцієнтів аі1 (і=2,3,...,n) шукають відмінний від нуля коефіцієнт аі1. Міняють це рівняння з першим. Такий коефіцієнт обов’язково знайдеться, інакше матриця вироджена, тобто detA=0.
Серед коефіцієнтів, на які відбувається ділення, можуть бути дуже малі, тоді при діленні на них можуть виникнути переповнення, що приведе до різкого зростання похибок.
|
|
|
При обчисленні визначника, треба виконати (n-1)×n! Операцій множення і (n!-1) – операцій додавання. Отже всіх операцій N=n!-1+(n-1)×n!=n×n!-1»n×n!
| n | |||
| N | 3.6×107 | 5×1019 | |
| час | 6 хв. | 1.4×1011год~5×109діб |
Якщо швидкодія 100000 оп/сек. Тому звичайні методи для обчислення визначника малоефективні. Тому стараються використовувати більш економні методи. Зручно використовувати прямий хід Гауса, тобто приводити матрицю до трикутного вигляду. Визначник при цьому не міняється, може змінитися тільки його знак і detA= ± 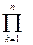 акк, де акк – діагональні елементи приведеної до ∆-вигляду матриці. Добуток береться зі знаком,,+’’, якщо кількість переставлених рядків парна, і,,-’’, якщо непарна (при приведенні до ∆-вигляду).
акк, де акк – діагональні елементи приведеної до ∆-вигляду матриці. Добуток береться зі знаком,,+’’, якщо кількість переставлених рядків парна, і,,-’’, якщо непарна (при приведенні до ∆-вигляду).
 Обчислення оберненої матриці
Обчислення оберненої матриці
1 k=j
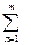 aik× zkj = dij 0 i¹j
aik× zkj = dij 0 i¹j
Для отримання оберненої матриці треба n-раз розв’язати початкову систему. Після кожного розв’язку системи знаходиться один стовпчик оберненої матриці. Наприклад, для знаходження стовпчика оберненої матриці номер j, тобто z1j,…,znj треба розв’язати систему таких лінійних рівнянь:
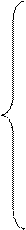 a11z1j + a12z2j +…+ a1nznj = 0
a11z1j + a12z2j +…+ a1nznj = 0
.
.
.
aj1z1j + aj2z2j +…+ ajnznj = 1 (2)
.
.
.
an1z1j + an2z2j +…+ annznj = 0
Щоб уникнути цього використовують модифікацію метода Гауса. Одну з таких модифікацій називають методом Гауса з вибором головного елемента в стовпці. Його відмінність від розглянутого метода Гауса в тому, що на кожному кроці шукається максимальний елемент в стовпці. Нехай на кожному кроці отримується діагональний елемент акк(к-1). Серед всіх елементів, які лежать вище шукаємо max: max aк(к-1).
Нехай цей елемент в рівнянні арк(к-1). Міняємо місцями р і k-е рівняння. Цю операцію повторюють на кожному кроці.
В ролі невідомих виступає стовпчик zij. В правій частині один стоїть тільки в z=j. Таких систем треба записати n-штук. Тут зручно проводити обчислення так як матриця aij – не міняється. Тому до трикутного вигляду систему приводять один раз. Для знаходження відповідного стовпчика використовують обернений хід методу Гауса. Цей метод ефективніший ніж метод:
|
|
|
(aij)-1 =  , де Aji – алгебраїчне доповнення до aij в початковій матриці. Таким методом для знаходження оберненої матриці треба виконати ~ n2n! операцій. А описаний метод з розв'язком систем лінійних рівнянь вимагає тільки ~ в 3 рази більше арифметичних операцій ніж приведення системи до трикутного вигляду.
, де Aji – алгебраїчне доповнення до aij в початковій матриці. Таким методом для знаходження оберненої матриці треба виконати ~ n2n! операцій. А описаний метод з розв'язком систем лінійних рівнянь вимагає тільки ~ в 3 рази більше арифметичних операцій ніж приведення системи до трикутного вигляду.
Важливим є питання точності отриманих розв’язків. Її характеризують двома величинами:
Похибка, яка рівна різниці між отриманим розв’язком і точним. При практичному розв’язуванні систем лінійних рівнянь за характеристику точності беруть нев’язку (величина, що дорівнює різниці між правою і лівою частиною рівняння, в яке підставляються розв’язки). Похибка e і нев’язка r взаємозв’язані. Якщо e = 0, то r = 0. Але обернене твердження не завжди справедливе. Нев’язка в практичних розрахунках повинна бути ~ 10-4 ¸ 10-6.
Метод ітерацій
Цей метод дозволяє отримати збіжну послідовність наближених значень. Не потрібно контролювати проміжні обчислення, тому що окремі помилки на будь-якому кроці ітерацій не деформують кінцевий результат, хоч можуть процес обчислення зробити довшим, тобто це метод – самовиправляючий.
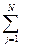 aijxj = bi, aii ≠ 0, визначник системи ≠ 0
aijxj = bi, aii ≠ 0, визначник системи ≠ 0
Виразимо з першого рівняння x1, з другого x2 і т.д. Поділивши рівняння на аіі отримаємо еквівалентну систему:
 x1 = β1+α12x2+α13x3+…+α1nxni
x1 = β1+α12x2+α13x3+…+α1nxni
x2 = β2+α21x2+α23x3+…+α2nxn
…
xn = βn+αn1x2+αn2x3+…+α n,n-1xn-1, де

- aij /aii, при i ≠ j
βi = bi/ aii; αi =
0, при i = j
або xi = βi +  αijxj (*)
αijxj (*)
назвемо її системою нормального виду.
Будемо розв'язувати її методом послідовних наближень. За нульове наближення візьмемо:
 x1(0) = β1
x1(0) = β1
x2(0) = β2
 …
…
xn(0) = βn
і підставимо в праву частину (*). Отримаємо:
xi(1) = βi +  αijxj(0), потім аналогічно
αijxj(0), потім аналогічно
xi(2) = βi +  αijxj(1)
αijxj(1)

 Робочі формули методу ітерацій
Робочі формули методу ітерацій
 xi(0) = βi
xi(0) = βi
xi(k+1) = βi +  αijxj(k)
αijxj(k)
αii = 0; i= 1,n; k=0,1,2,…
Збіжність?! Якщо  |αij| < 1 (i=1,n) або |аij| >
|αij| < 1 (i=1,n) або |аij| > 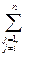 |аij| (i=1,n), то метод ітерацій для всіх рядків буде збіжним.
|аij| (i=1,n), то метод ітерацій для всіх рядків буде збіжним.
При обчисленні на машині процес ітерації закінчують, якщо
 |x
|x 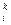 - x
- x 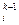 | ≤
| ≤  •ε (i=1, n)
•ε (i=1, n)
q= 
 |αij| < 1
|αij| < 1
Доводять, що тоді |x  - x
- x 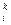 | ≤ ε
| ≤ ε
|
|
|
|
|
Дата добавления: 2015-05-23; Просмотров: 811; Нарушение авторских прав?; Мы поможем в написании вашей работы!