Метричний тензор у косокутних координатах 1 страница

Знайдемо формули переходу від узагальнених складових до узагальнених проекцій і навпаки.

Помножимо рівність

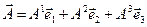
скалярно на , тоді

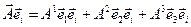(17.1)

Введемо позначення

(17.2)

Дев’ять величин бедемо називати складовими метричного тензора. Якщо 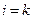, то

, (17.3)

– величини характеризують довжини відповідних масштабних векторів. При

(17.4)

величини визначають прямокутну матрицю

-62-

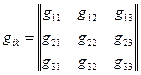
(17.5)

однак, з дев’яти елементів істотно різних є тільки шість. Це тому, що

(17.6)

Геометричний зміст величини полягає в тому, що вони є узагальненими проекціями масштабних векторів на самих себе.

Якщо масштабні вектори одиничні, то – просто косинуси кутів між осями координатної системи. Зокрема, для прямокутної системи координат

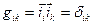, (17.7)

Приклад. Плоска косокутна система задана масштабними векторами

,

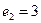що утворюють кут .

Компоненти метричного тензора тоді визначають матрицю

Повернемось до формули (17.1). використовуючи вирази можемо написати

,

тобто

, (17.8)

Ця група формул дозволяє знати унікальні проекції вектора, якщо відомі його узагальнені складові і компоненти метричного тензора.

Розглянемо тепер формулу

.

Обидві її сторони помножимо скалярно на

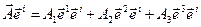. (17.9)

Введемо дев’ять величин

-63-

, . (17.10)

які також будемо називати компонентами метричного тензора. Надалі

будемо називати коваріантним складовим матеріального тензора,

– його контраваріантним складовими. Сенс цих термінів стане зрозумілим пізніше.

Формулу (17.9) можна записати

. (17.11)

Дев’ять величин (чи відповідно ) характеризують метрику косокутного простору. Якщо задана матриця є діагональною, тобто

то зрозуміло, що система прямокутна (але масштаби не обов’язково одиничні).

Таким чином, косокутну систему координат можна задати трьома масштабними векторами , або дев’ятьма (точніше–шістьма) величинами . Зв’язок між і задають формулами (17.2) і (17.3)

Знайдемо групу формул, які зв’язують масштабні вектори в дуальними через складові метричного тензора. Будемо виходити з рівності

.

Замість підставимо сюди вираз (17.8).

.

Звідси випливе, що

,

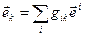або в більш конкретному записі

. (17.12)

Аналогічно знайдемо

, (17.13)

Таким чином, ми маємо три групи формул, що зв’язують масштабні і дуальні вектори

-64-

= i,k=1,2,3 /1/

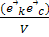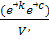= , = (I,k,c) /2/
= , =∑ i=1,2,3 /3/

Найбільшим ступенем невігластва є фальшива наука.

Алі бен Марабу

10. Скалярний і векторний добуток двох векторів в косокутних координатах.

Розглянемо два вектори А⃗= , В⃗=

І обчислюю їх скалярний добуток А⃗В⃗= ∑і ∑к =∑і ∑к

Якщо врахувати, що ∑к

А⃗В⃗=∑i

Вектори А⃗ і В⃗ можна записати також у вигляді А⃗= , В⃗=

Тоді А⃗В⃗= ∑і ∑к =∑і ∑к ,

А тому, що ∑к

То справедлива також формула А⃗В⃗=∑i

Таким чином, для скалярного добутку двох векторів у косокутних координатах маємо чотири формули

А⃗В⃗= ∑і ∑к /18.1/

-65-

А⃗В⃗= ∑і ∑к , /18.2/

А⃗В⃗=∑i /18.3/

А⃗В⃗=∑i /18.4/

Розглянемо тепер вираз для векторного добутку векторів А⃗ і В⃗

=∑і ∑к[ .

З дев'ятки доданків у цій подвійній сумі три доданки дорівнюють нулеві. Дійсно, [ 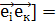0 і=к

Далі маємо [ -[ ],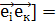

Отже = () /18.5/

Правильність такого запису перевіряють безпосередньо. Розглянемо два з шести доданків ] +[ ] = ](

Тому

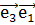= ]( +[ ]( +[ ](. /18.6/

Якщо згадаємо формулу [ 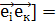V , (I,k,c)

То маємо ще один запис векторного добутку в косокутих координатах

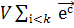= () / 18.7/

або в розгорнутому вигляді

= ( +V ( + (. /18.8/

Запишемо ще раз формулу для скалярного добутку векторів

А⃗В⃗=∑і ∑к \

І врахуємо, що

Тоді А⃗В⃗=∑к = .

-66-

З другого боку =

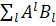
отже, повинна задовольнятися рівність

= I,l=1,2,3 /18.9/

Де - символ Кронекера / ми вводимо нове позначення замість ,доцільність такого поняття стане зрозумілою в наступному параграфі/.

Формули /18.9/ встановлюють зв'язок між коваріантними і контрваріантними складовими матричного тензора. Якщо відомі коваріантні складові , то /18.9/ можна розглядати як систему лінійних алгебраїчних рівнянь для визначення

І=1 l=1

I=1 l=2 , і т.д.

Згідно з теоремою Крамера розв'язки цієї системи дорівнюють

= , /18.10/

Де g=dct / -детермінант, підрахований з елементів матриці .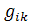

Переконаємось, що g= /18.11/

Де V- об’єм паралелепіпеда, побудованих на масштабних векторах. Використовуючи тотожність Лагранжа одержуємо

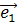= ( [ ])( ])= =dct =g

=( [ ])( ])= =det/ .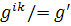

-67-

Уява важливіша від знань.

А. Ейнштейн

19. Правила індексів

Запишемо ще раз окремі формули, одержані в попередніх параграфах:

, (𝛼) , /𝛾/
, (𝛽) , /𝛿/

А⃗В⃗=∑і ∑ = ∑і ∑ /𝜀/

Якщо уявно придивитись до цих формул,як і зрештою до всіх інших формул попередніх трьох параграфів,то можна завважити певні законо-мірності для індексів у формулах. Таких закономірностей є чотири.

1.Якщо якийсь індекс фігурує в лівій стороні формули один раз, то він фігурує в правій стороні формули також один раз. Якщо зліва індекс знаходиться знизу,то і в правій стороні формули цей індекс знаходиться знизу. Якщо індекс знаходиться зверху, то він знаходиться зверху в обох сторонах формули. Такий індекс називають рухомим індексом,його можна позначити довільною буквою.

Прикладами на це правило є формули /𝛼-𝛿/,де рухомим індексом є індекс і. Ці ж формули можна записати

, ,

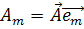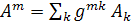, . m=1,2,3.

2.Формула залишається справедливою, якщо в обох її сторонах підняти рухомий індекс знизу вверх. Наприклад, формула (𝛽) одержується підніманням рухомого індекса і в формулі (𝛼).

Справедливе і обернене. Наприклад, оускаючи два рухомі індекси і,к в формулі

Одержемо I,k=1,2,3 3.

Якщо якийсь індекс знаходиться під знаком суми, то він зустрічається обов’язково два рази: один раз знизу і один раз зверху. Такий індекс називають німим індексом, його можна позначити довільною буквою.

-68-

Прикладом німого індекса є індекс к в формулі

,

Цю ж формулу можна записати ,

У формулі (𝜀)виступають два німі індекси і,к.

Формула/18.5/ не є винятком з цього правила. Індекс ℓ зв’язаний з індексом і,к правилом циклічної перестановки.

4.Формула залишається справедливою, якщо німий індекс в одному місці опустити і в другому підняти. Наприклад,справедливими є формули

А⃗В⃗=∑i , А⃗В⃗=∑i І також формули

А⃗В⃗=∑і ∑ , А⃗В⃗= ∑і ∑

Закономірності і/ -4/ зважив Ейнштейн в 1916 році. Він запропонував правило, яке дозволяє записувати формули в більш простому і компактному виляді / правило підсумовування Ейнштейна/.

Якщо один і той же індекс входить в який-небуть одночлен двічі, один раз зверху, а другий раз знизу, то написаний вираз означає суму одночленів, в яких цей індекс пробігає всі значення від І до 3/в n-вимірному просторі- відІ до n/. Наприклад,

Таким чином, формули /18.1/ - /18.4/ можна записати

А⃗В⃗= , А⃗В⃗= ,.

А⃗В⃗ , А⃗В⃗=

З другого боку, користуватись правилом Ейнштейна вимагає певни навиків /треба розуміти символ суми там, де він не фігурує/. Тому в нашому курсі цим правилом користуватися не будемо.

Повернемось ще раз до формул , ,

Перша з них визначає правило опускання індекса: щоб опустити індекс у величині досить застосувати оперетор /19.1/

-69-

Тобто, досить помножити 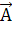на коваріантний матричний тензор і підсумувати по індексу к.

Аналогічно друга з формул /19.1/ визначає правило піднімання індекса, яке зводиться до множення на контраваріантний матричний тензор і відповідного сумування.

узагальнені проекції і узагальнені складові вектори. Нехай, наприклад, маємо вираз . Ми можемо одержати є нього вираз опускаючи індекс і. =

Вчимось на помилках. Є народи,

що вчаться на досягнення.

А. Качановський

20. Диференціальні операції в косокутних координатах.

У косокутній системі координат,визначеній масштабними векторами

Розглянемо довільну точку з координат

Ці три величини як видно з рис. 62, / рисунок правильний якщо вектори одиничні /, в узагальненими складовими радіуса – вектора , = /20.1/

МИ бачимо,що позначення для косокутних координат точки є невдалими. Для більш конкретного запису формул треба ввести позачення

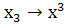, , , тоді + +

Нехай в косокутних системах задана функція

φ= φ(x,y,z) = φ(, , )

яка в точці М має значення φ(, , ) і в близькій точці М' – значення

φ=(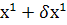, , 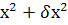) = φ(, , )+𝛿φ.

-70-

З точністю до малих величин вищого порядку

𝛿φ= 𝛿 + 𝛿 + 𝛿 = .

Отриманий вираз можна інтерпретувати як скалярний добуток двох векторів А⃗В⃗=∑i ,

де

Тоді 𝛿φ=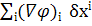

Таким чином, у косокутних координатах величини

= /20.2/

Інтерпретуються як узагальнені проекції градієнта скалярної функції, Символічно 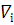= , /20.3/

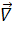= + + . /20.4/

Легко знайти узагальнені складові вектора набла. Для цього досить піднести індекс у величин

= /20.5/

Нехай у косокутній системі задане векторне поле

Щоб знайти вираз для дивергенції вектора 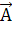досить згадати що

div =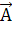

Тоді div = = ,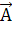

div 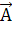= + + 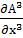. /20.6/

Аналогічно можна знайти вираз для ротора векторного поля в косокутних координатах. Для цього використовують формулу

-71-

rot = [ ]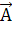

Дата добавления: 2015-05-24