
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Числові послідовності. Границя послідовності
|
|
|
|
Якщо кожному числу п з натурального ряду чисел 1,2...п,... поставлено у відповідність дійсне число 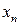 , тоді множина дійсних чисел
, тоді множина дійсних чисел 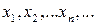 називається числовою послідовністю.
називається числовою послідовністю. 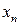 – загальний елемент послідовності
– загальний елемент послідовності 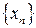 , п – його номер.
, п – його номер.
Послідовність вважається заданою, якщо вказаний спосіб отримання будь-якого її елемента, наприклад, формула 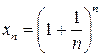 задає послідовність 2,
задає послідовність 2, 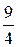 ,...
,...
Послідовність 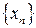 , називається обмеженою, якщо існують такі числа т і М
, називається обмеженою, якщо існують такі числа т і М 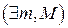 , що будь-який елемент
, що будь-який елемент 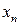
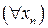 цієї послідовності задовольняє нерівності:
цієї послідовності задовольняє нерівності: 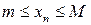 . Число
. Число 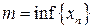 – найменше значення
– найменше значення 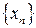 , а число
, а число 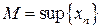 – найбільше значення
– найбільше значення 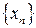 .
.
Послідовність 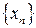 називається необмеженою, якщо
називається необмеженою, якщо 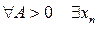 цієї послідовності, який задовольняє нерівність:
цієї послідовності, який задовольняє нерівність: 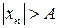 .
.
Число а називається границею послідовності 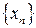 , якщо
, якщо 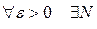 , що
, що 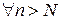 виконується нерівність
виконується нерівність 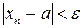 .
.
Послідовність 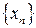 , яка має границю а, називається збіжною:
, яка має границю а, називається збіжною:
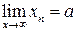 або
або 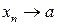 при
при 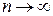 (3)
(3)
Послідовність, яка не є збіжною, називається розбіжною.
Приклад 1. Користуючись означенням границі послідовності, доведемо, що 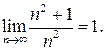
Згідно з означенням: 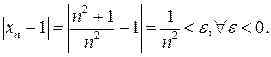 Звідси випливає, що як номер N можна взяти будь-яке ціле число, яке задовольняє нерівність
Звідси випливає, що як номер N можна взяти будь-яке ціле число, яке задовольняє нерівність 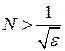 . Тоді нерівність
. Тоді нерівність 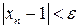 буде виконуватись
буде виконуватись 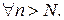
Приклад 2. Знайти 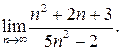
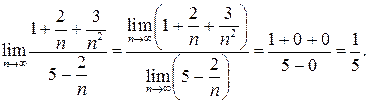
Послідовність 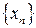 називається зростаючою
називається зростаючою 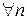 , якщо
, якщо 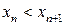 ; неспадною, якщо
; неспадною, якщо 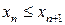 ; спадною, якщо
; спадною, якщо 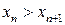 ; незростаючою, якщо
; незростаючою, якщо 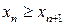 . Усі такі послідовності називаються монотонними. Монотонна обмежена послідовність збігається (за теоремою).
. Усі такі послідовності називаються монотонними. Монотонна обмежена послідовність збігається (за теоремою).
Приклад 3.
1. 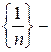 спадна і обмежена (m= 0, M= 1).
спадна і обмежена (m= 0, M= 1). 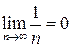 .
.
2. 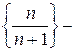 зростаюча і обмежена (m=
зростаюча і обмежена (m= 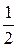 , M= 1).
, M= 1). 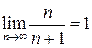 .
.
3. 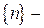 зростаюча і необмежена.
зростаюча і необмежена.
4. 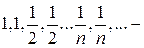 незростаюча і обмежена (m= 0, M= 1).
незростаюча і обмежена (m= 0, M= 1).
5. 1,1,2,2,... n, n... – неспадна і необмежена.
6. 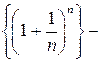 зростаюча і обмежена (m= 2, M=е).
зростаюча і обмежена (m= 2, M=е).
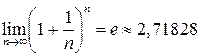 (число е).
(число е).
|
|
|
|
|
Дата добавления: 2015-05-24; Просмотров: 473; Нарушение авторских прав?; Мы поможем в написании вашей работы!