
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Асимптоти графіка функцій
|
|
|
|
Дослідження функції на екстемум.
Формула Тейлора.
Нехай функція 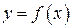 має в точці
має в точці 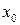 і деякому її околі похідні порядку п +1. Це означає, що функція
і деякому її околі похідні порядку п +1. Це означає, що функція  та її похідні до порядку п включно неперервні і диференційовні в цьому околі. Тоді справедлива формула Тейлора
та її похідні до порядку п включно неперервні і диференційовні в цьому околі. Тоді справедлива формула Тейлора
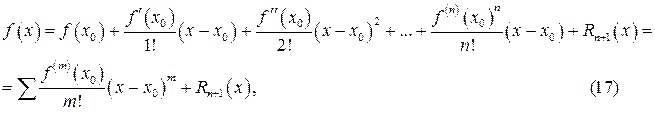 де
де 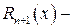 деякий залишковий член, причому
деякий залишковий член, причому 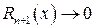 при
при 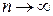 (0!=1 у формулі (17)).
(0!=1 у формулі (17)).
Отже, формула Тейлора надає можливість розкласти функцію  у степеневий ряд в околі деякої точки
у степеневий ряд в околі деякої точки 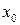 .
.
Зауваження. Формулою Маклорена називають формулу Тейлора (17) при 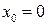 .
.
Приклад 1. Знайти 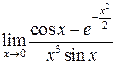 .
.
Маємо невизначеність 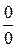 . Розкладемо функції
. Розкладемо функції 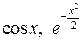 і
і 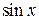 у ряд Маклорена з необхідною точністю:
у ряд Маклорена з необхідною точністю:
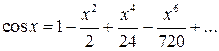
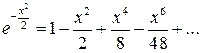
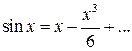
Тоді маємо:
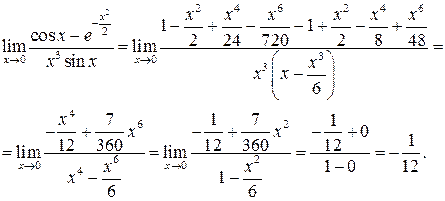
Приклад 2. Знайти 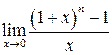 .
.
Маємо невизначеність 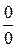 . Розкладемо функцію
. Розкладемо функцію 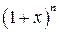 в ряд Маклорена:
в ряд Маклорена: 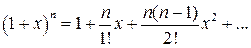 У результаті отримуємо:
У результаті отримуємо:
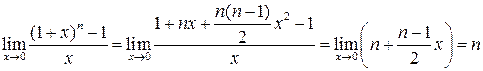 .
.
Нехай функція 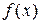 диференційована на інтервалі
диференційована на інтервалі 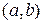 . Точка
. Точка 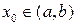 називається точкою екстремуму, якщо
називається точкою екстремуму, якщо 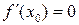 .
.
Точка екстемуму 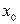 називається локальним мінімумом (максимумом), якщо
називається локальним мінімумом (максимумом), якщо 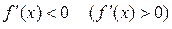 ліворуч від цієї точки і
ліворуч від цієї точки і 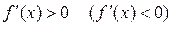 праворуч від цієї точки.
праворуч від цієї точки.
Крім того, у точці локального мінімуму (максимуму) справедливе співвідношення 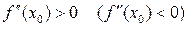 .
.
Точка 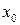 називається точкою перегину, якщо 1)
називається точкою перегину, якщо 1) 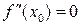 і 2)
і 2) 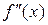 має різні знаки ліворуч і праворуч від точки
має різні знаки ліворуч і праворуч від точки 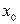 .
.
Приклад 1. Дослідити функцію 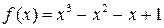 на екстремум.
на екстремум.
 Знаходимо похідну і прирівнюємо її нулю:
Знаходимо похідну і прирівнюємо її нулю: 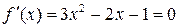 . Отже, точками екстремуму є
. Отже, точками екстремуму є 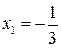 і
і 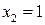 . Відмітивши їх на осі х (Рис. 3.1), дослідимо на її верхній частині знак похідної функції
. Відмітивши їх на осі х (Рис. 3.1), дослідимо на її верхній частині знак похідної функції 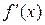 в околі цих точок екстремуму, а в її нижній частині – інтервали монотонності даної функції. У результаті маємо: на інтервалі (
в околі цих точок екстремуму, а в її нижній частині – інтервали монотонності даної функції. У результаті маємо: на інтервалі (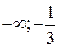 )
) 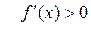 (функція
(функція 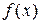 зростає), на інтервалі
зростає), на інтервалі 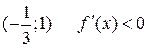 (функція
(функція 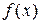 спадає), і, нарешті, на інтервалі
спадає), і, нарешті, на інтервалі 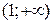
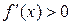 (функція
(функція 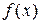 знову зростає). Це означає, що функція
знову зростає). Це означає, що функція 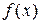 у точці
у точці 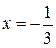 має локальний максимум
має локальний максимум 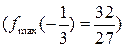 , а у точці х= 1 – локальний мінімум
, а у точці х= 1 – локальний мінімум 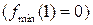 . Дійсно,
. Дійсно, 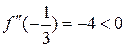 і
і 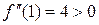 .
.
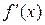 + max – min +
+ max – min +
|
|
|





 x
x
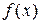
 1
1
Рис. 3.1. Дослідження функції 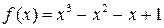 на екстремум
на екстремум


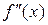 – +
– +
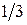 х
х
Рис. 3.2. Дослідження функції 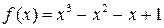 на перегин
на перегин
Дослідимо, чи має дана функція точку перегину. Для цього знайдемо другу похідну і прирівняємо її до нуля: 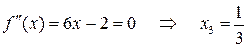 . З
. З
Рис. 3.2 видно, що 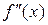 має різні знаки ліворуч і праворуч від точки
має різні знаки ліворуч і праворуч від точки 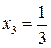 і, отже, дана точка є точкою перегину функції
і, отже, дана точка є точкою перегину функції 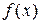
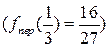 . Її графік наведено на Рис. 3.3.
. Її графік наведено на Рис. 3.3.
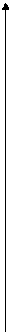 |



 4 у
4 у
 |
2 
 |

 0
0 
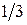 1 х
1 х
 |
 -2
-2
 | |||
 |
-4
-2 -1 0 1 2
Рис. 3.3. Графік функції 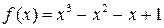
|
|
|
|
|
Дата добавления: 2015-05-24; Просмотров: 517; Нарушение авторских прав?; Мы поможем в написании вашей работы!