Лекція 10

Атом водню. Дискретний спектр

Розглянемо рух електрона у кулонівському полі „нерухомого” атомного яд­ра з потенціальною енергією

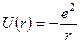. (10.1)

У лекції 7 ми розглянули рівняння Шредінґера для однієї частинки масою m з координатою 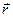у сферично симетричному полі з потенціальною енергією 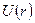. Змінні у рівнянні розділяються (відокремлюються), і, відповідно до цього, хвильова функція 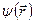у сферичних координатах 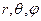зображується у вигляді добутку

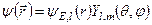, (10.2)

У випадку атома водню радіальне рівняння Шредінґера, якому задовольняє функція 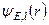, має вигляд

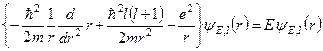. (10.3)

Зробимо підстановку

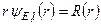. (10.4)

Для функції 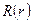одержуємо одновимірне рівняння Шредінґера

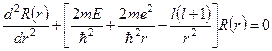. (10.5)

Введемо т. з. борівський радіус

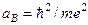(10.6)

і характерний масштаб виміру енергії

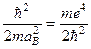, (10.7)

який названо рідбергом:

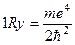. (10.8)

Числові значення цих величин рівні:

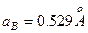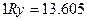, еВ. (10.9)

Перейдемо у рівнянні (10.5) до безрозмірних величин:

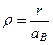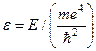, . (10.10)

Тоді рівняння (10.5) набуде вигляду:

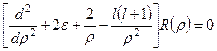. (10.11)

Дослідимо розв’язок рівняння (10.11) для великих значень ρ при від’ємних зна­ченнях повної енергії E. При 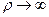у рівнянні (10.11) з E <0 можна знехтува­ти третім і четвертим доданками. Таким чином, асимптотичний розв’язок рів­нян­ня (10.11) при 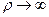та E <0 матиме вигляд

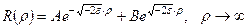. (10.12)

Оскільки хвильова функція при нескінченно великих відстанях ρ не може зростати до нескінченності, у формулі (10.12) слід покласти B =0. Отже, розв’язок рівнян­ня (10.11) при від’ємних значеннях повної енергії E слід шукати у вигляді

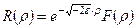, (10.13)

де функція представляється степеневим рядом

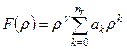. (10.14)

Визначимо асимптотичну поведінку функції 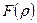при 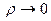. Для цього підста­вимо вираз (10.13) у рівняння (10.11), зберігаючи при цьому у розкладі (10.14) доданки з найменшими степенями ρ. Це означає, що при 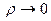функцію 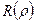представимо у вигляді:

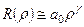. (10.15)

Після підстановки цього виразу у формулу (10.11), одержимо рівняння для визначення γ:

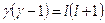. (10.16)

Звідси випливає наявність двох розв’язків для γ:

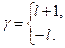(10.17)

Щоб функція 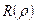прямувала до нуля при 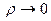, треба взяти тільки один розв’язок, а саме 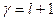. Адже, для різних значень l функція 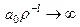, коли .

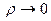Отже, розв’язок рівняння (10.11) при від’ємних значеннях повної енергії E, який задовольняє граничні умови у нулі та на нескінченності, слід шукати у вигляді:

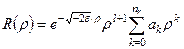. (10.18)

Підставимо вираз (10.18) у рівняння (10.11) і прирівняємо коефіцієнти при однакових степенях 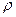. Отримаємо рекурентне співвідношення

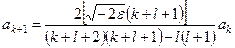. (10.19)

Це співвідношення дозволяє виразити послідовно всі коефіцієнти степене­вого ряду (10.14) через значення a ₀, яке визначається з умови нормування хвильової функції. Нам слід обмежити число членів ряду (10.18). Умовою того, що степеневий ряд буде обірваний на члені з k = n_r, є умова 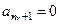. Отже,

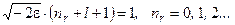(10.20)

З формул (10.10) та (10.20) отримуємо рівняння, що фіксує можливі рівні енер­гії (знаменита формула Н.Бора):

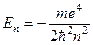, (10.21)

де n = n_r + l +1. Оскільки орбітальне квантове число l =0, 1, 2,…, тоді головне кван­тове число n набуває цілих додатних значень, починаючи з одиниці:

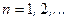(10.22)

Максимально можливе значення числа l при заданому n отримуємо, якщо n_r =0:

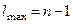. (10.23)

Отже, l =0, 1, 2,…, n -1.

Стани з певним значеням енергії 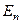і певним значенням орбітального мо­мента скорочено позначаються через 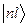. При цьому замість квантового числа l використовують позначення: випадку l =0 відповідає s -стан, випадку l =1 –
p -стан, випадку l =2 – d -стан, випадку l =3 – f -стан, випадку l =4 – g -стан, і т.д.

Кратність виродження. У загальному випадку кожному рівню з головним квантовим числом n відповідає n станів, які відрізняються різними значеннями квантового числа l, а саме: l =0, 1, 2,…, n -1. Кожний стан з певним значенням l має виродження, кратність якого рівна числу (2 l +1). Такі стани мають різні значення квантового числа m: 0, ±1, ±2,…, ± l. Через це за­гальна кратність виродження стаціонарного стану атома водню з квантовим числом n буде рівна

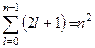. (10.24)

Наведемо в Таблиці 10.1 приклади перших радіальних функцій атома водню, які нормовані умовою

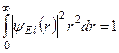. (10.25)

Таблиця 10.1

Стани	nr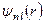
1 s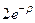
2 s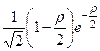
2 p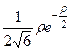
3 s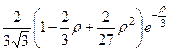
3 p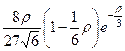
3 d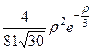

Радіальні функції водню

У загальному випадку довільного стану його нормовані радіальні хвильові функції виражаються через т.з. приєднані поліноми Лагера:

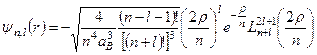, (10.26)

де одне із стандартних означень приєднаного полінома Лагера є таким

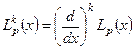, (10.27)

а поліном Лагера

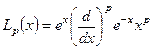. (10.28)

Ще раз нагадаємо, що повна хвильова функція

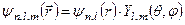
повинна нормуватись на одиницю, тобто

,

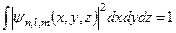а у сферичних координатах:

.

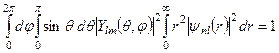Цими формулами завершується розв’язок квантовомеханічної задачі про рух електрона в полі кулонівського потенціалу для зв’язаних станів (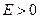, проблема Кеплера).

Основний стан атома водню: 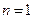, , , 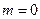а його хвильова функція

.

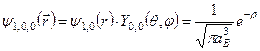Відповідно енергія основного стану .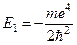

Перший, 4-кратновироджений, збуджений стан водню:

, , ; , , ;

, , ; , , .

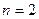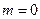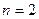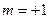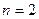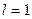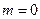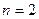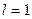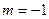Енергії цих збуджених станів відповідають такі чотири хвильові функції:

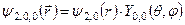
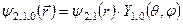
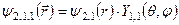
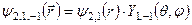
Кутові функції цих станів мають вигляд:

;

,

.

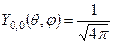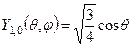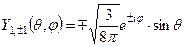Радіальні функції одержуємо із загального виразу для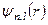

,

,

, .

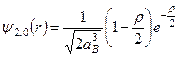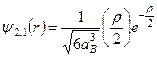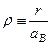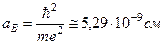Радіальні функції 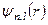визначають густину імовірності 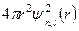розподі­лу „електронної хмари” вздовж радіуса .

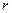Наприклад, для основного стану густина імовірності

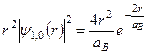
має максимум значення при 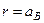. Це означає, що величина 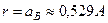дозволяє прикинути величини просторових розмірів атома.

Дата добавления: 2015-06-04