Доказательство. Пусть Q – совокупность всех функций из , непрерывных относительно сдвига. Очевидно, что Q – линейное подпространство R. Покажем, что Q замкнуто в R

Доказательство. В силу условия 1) при. Но тогда и при каждом фиксированном значении индекса k имеем.

Лемма. Если для некоторой функции разложение сходится по норме пространства, то – есть обычные коэффициенты Фурье функции.

Лемма доказана.

Лемма. Всякая функция f(x), входящая в однородное пространство 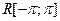, непрерывна относительно сдвига по норме: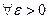 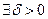: при 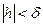выполнено .

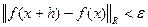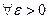
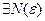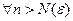
Пусть в R, то есть : . Подберем 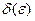из условия непрерывности относительно сдвига функции 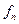так, чтобы иметь при 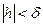. В силу условия 2) одновременно имеем 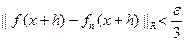. Отсюда

.

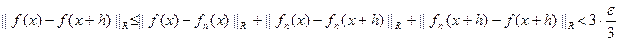То есть f тоже непрерывна относительно сдвига.

Наконец заметим, что каждая из функций 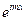непрерывна относительно сдвига, так как .

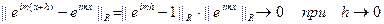Таким образом, Q содержит тригонометрические полиномы и замкнуто. Отсюда в силу условия 3) Q = R.

Лемма доказана.

Теперь можем сформулировать основные проблемы:

А. Дана функция f(x) из однородного пространства 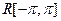и вычислены ее коэффициенты Фурье 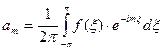. Будет ли ряд Фурье 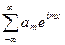сходиться к функции 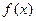по норме пространства ?

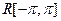Ответ на этот вопрос, вообще говоря, отрицательный. Существуют однородные пространства, и при том самые привычные нам, как и , в которых ряд Фурье для некоторых функций расходится.

Такой ответ вызывает естественное пожелание:

Б. Указать по возможности простой единообразный процесс, позволяющий эффективно восстанавливать функцию f(x) по ее ряду Фурье, невзирая на возможную расходимость этого ряда.

Теорема. Для любой функции 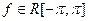средние арифметические частных сумм

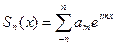ее ряда Фурье сходятся по норме пространства 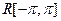к функции f(x) при .

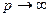Доказательство теоремы. Положим , где – частная сумма ряда Фурье для функции .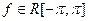

.

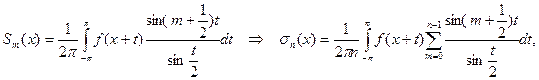
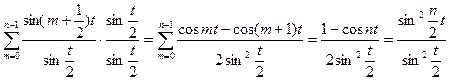Итак, . (*)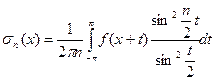

Функция 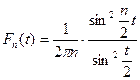называется ядром Фейера. В отличие от ядра Дирихле ядро Фейера неотрицательно. Далее, если 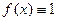, то 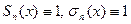и, значит, .

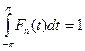Теперь непосредственно переходим к доказательству теоремы. Проверим сначала, что она справедлива для любого тригонометрического полинома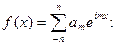

,

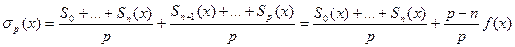поскольку частные суммы при q > n совпадают с многочленом 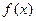. Далее, при 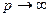первое слагаемое стремится к нулю, а второе – к 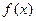. Рассмотрим теперь общий случай 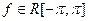. Равенство (*) задает как действие линейного интегрального оператора с ядром Фейера на функцию f. Обозначим этот оператор через А_n.

.

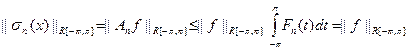Здесь неравенство является аналогом известного неравенства для скалярных функций. Для функций вещественного аргумента t, принимающих значения в линейном нормированном пространстве R, можно построить по стандартной схеме интеграл Римана (рассматриваются только непрерывные функции аргумента t). При этом сохраняются все известные свойства интеграла Римана и, в частности, если g(t) – абстрактная непрерывная функция, 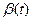– скалярная непрерывная функция, то – снова абстрактная непрерывная функция и в случае имеет место неравенство .

В данном случае g(t) = f(x + t) ставит в соответствие каждому вещественному значению t функцию переменного x – элемент пространства R.

Итак, для любого n .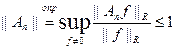

Теперь доказательство теоремы завершается на основании простого утверждения.

Лемма. Пусть в линейном нормированном пространстве R задана последовательность линейных операторов А_n, нормы которых ограничены фиксированной постоянной М. Если предельное соотношение 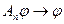справедливо для элементов 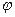, принадлежащих некоторому всюду плотному множеству 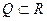, то оно справедливо и для всех элементов .

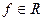Доказательство леммы. Пусть 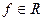и задано . Найдем 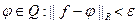. Затем найдем 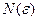так, что 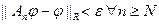. Тогда .

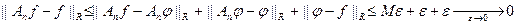Лемма доказана.

Доказанная теорема в применении к пространству приводит к следующему результату: всякая функция 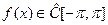есть предел равномерно сходящейся последовательности средних арифметических частных сумм своего ряда Фурье. В этом частном виде теорема была доказана в 1905 году Л.Фейером.

В применении к пространству эта теорема приводит к важному свойству единственности: если все коэффициенты Фурье суммируемой функции f равны 0, то f= 0 почти всюду на .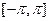

Для пространства 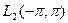последний результат означает, что система функций полна в этом пространстве: если для какой-либо функции из равенства нулю всех ее коэффициентов Фурье следует, что g(x) = 0 почти всюду в 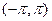, то система полная.

Дата добавления: 2015-07-02