Часть 2. Опыт показывает, решение дифференциальных уравнений в численном виде приводит к тому, что студенты не понимают принципиального отличия нелинейных систем от

Опыт показывает, решение дифференциальных уравнений в численном виде приводит к тому, что студенты не понимают принципиального отличия нелинейных систем от линейных. Аналитическое решение подчеркивает это различие, численное – стирает. Поэтому представляется полезным провести некоторое исследование свойств обоих типов уравнений.

Дифференциальное уравнение порядка n

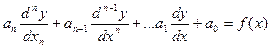
называется линейным, если все его коэффициенты 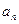(n =0,1,…) являются числами или функциями аргумента х.

Дифференциальное уравнение называется нелинейным, если хотя бы один из этих коэффициентов зависит от функции у, или ее производных.

Рассмотрим линейное дифференциальное. уравнение второго порядка

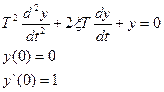
Данное дифференциальное уравнение является линейным с постоянными коэффициентами, так как и Т и x - числа. В теории автоматического управления линейное уравнение, записанное в такой форме, называется типовым динамическим звеном второго порядка.

1. Исследуем влияние на решение коэффициента x. Его значения при Т= 10 заданы в таблице:

T	ξ
	0.5
	-0.5

Убедимся, что

при x =5 решение - монотонно затухающая кривая,

при x =0,5 - решение затухающее колебательное,

при x =0 решение - чистая синусоида, при

x = -0,5 решение расходящаяся синусоида и, наконец,

при x = -5 решение - монотонно расходящаяся кривая.

Следовательно, если данным дифференциальным. уравнением описывается какая - либо реальная система (а это бывает сплошь и рядом), то при x= 0,-0.5, -5 система неработоспособна, т.к. является неустойчивой.

Коэффициент x в данном уравнении называют коэффициентом затухания.

3. Исследуем теперь влияние коэффициента Т при неизменном x = 0.5.

Примем Т= 1, 5,10,25. Убедимся, что увеличение Т ведет к увеличению запаздывания системы. Коэффициент Т называют линейным запаздыванием.

1. Если в любом дифференциальном уравнении и правая часть равна 0 и заданы нулевые начальные условия, то его решение будет также тождественно равно 0.Начальные условия и правая часть являются возмущениями. Рассмотрим, как влияет величина начальных условий - возмущений на решение дифференциального уравнения. При Т= 10, x = 0.5 рассмотрим решения для у₀ = 10 и y₀ =100.

Мы видим, что характер решения не изменился, устойчивая система продолжает оставаться устойчивой при увеличении возмущений.

Пример решения линейного уравнения. Задано одно и то же уравнение, но разные начальные условия (различное возмущение).

3d²y/dt² +0,8dy/dt +6y=0 3d²z/dt² +0,8dz/dt +6z=0

t₀ =0, y₀= 10, dy/dt _t=0 =0 t₀ =0, z₀ =100, dz/dt _t=0 =0

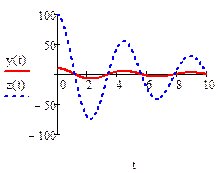
Рис.1 Влияние начальных условий на решение линейного дифференциального уравнения.

Характер решения не изменился. В обоих случаях - затухающие колебания с одинаковой частотой.

Задача 1.

А)Решить приведенное выше линейное дифференциальное уравнение для Т=10 и ξ= -2,-0.5, 0, 0.5,5.

Убедиться, что:

При ξ - -2 решение – расходящийся апериодический процесс;

при ξ = -0.5 – решение – расходящийся периодический процесс;

при ξ =0 – решение незатухающие гармонические колебания;

при ξ= +0.5 – решение затухающие колебания;

при ξ = +5 – решение апериодический сходящийся процесс.

Б). Решить приведенное выше линейное дифференциальное уравнение для ξ=2 и

Т=0.5,5,10.

Убедиться, что увеличение коэффициента линейного запаздывания Т приводит к уменьшению наклона решения - экспоненты.

В) Решить приведенное выше линейное дифференциальное уравнение для начальных условий, заданных на рис.1. Убедиться, что характер решения и период колебаний не изменился.

Дата добавления: 2015-06-27