Общие сведения. Качественное описание задачи распознавания

Качественное описание задачи распознавания.

Распознавание - процесс преобразования входной информации, в качестве которой рассматриваются некоторые параметры (признаки распознаваемых образов), в выходную, представляющую собой заключение о том, к какому классу относится распознаваемый образ. Задачу распознавания можно представить в следующей трактовке.

Пусть имеется некоторая совокупность объектов или явлений. В соответствии с выбранными принципами классификации она подразделена на ряд классов. Например, при распознавании диспетчерской службой аэропорта прибывающих самолетов различаются классы: пассажирские, транспортные, спортивные и т.д. Разработан словарь признаков и с его помощью описываются классы объектов, т.е. на основе априорных данных (предыдущего опыта) устанавливается связь между классами и признаками (априорная информация). Например, признаки для самолетов: максимальная скорость, предельная высота полета, число и тип двигателей, размах крыльев и т.п.

Появляется объект, подлежащий распознаванию, вместе со сведениями о присущих ему признаках (апостериорная информация).

Необходимо определить к какому классу может быть отнесен данный объект.

Распознавание сложных объектов и явлений требует создания специальных систем распознавания. Система распознавания - сложная динамическая система, включающая в свой состав коллектив специалистов и совокупность технических средств получения и переработки информации и предназначенная для решения на основе специально сконструированных алгоритмов задач распознавания соответствующих объектов или явлений.

Логические задачи распознавания. В проблеме распознавания объектов методы алгебры логики (исчисления высказываний) выступают на первый план в случаях, когда отсутствуют сведения о количественном распределении объектов по пространственным, временным, энергетическим и другим интервалам в соответствующем пространстве признаков, а в распоряжении исследователя имеются лишь детерминированные логические связи между рассматриваемыми объектами и их признаками. Задачи распознавания, удовлетворяющие этим условиям, называются логическими задачами распознавания.

Пример [3]. В результате продолжительных наблюдений за воздушным противником установлено‚ что на выполнение боевого задания направляется следующий состав авиационных средств:

- либо появляются истребители-перехватчики и штурмовики и при этом нет ни тяжелых бомбардировщиков, ни истребителей сопровождения;

- либо появляются тяжелые бомбардировщики и истребители сопровождения и нет истребителей-перехватчиков, причем легкие бомбардировщики и штурмовики появляются одновременно.

На основании этих данных‚ образующих априорную информацию‚ требуется определить, например:

а) какие выводы можно сделать относительно появления бомбардировщиков‚ если известно‚ что ожидается налет, в котором будут участвовать истребители сопровождения и не будет штурмовиков;

б) что можно сказать о возможности появления истребителей и штурмовиков‚ если известно‚ что в налете вообще не будут участвовать бомбардировщики‚ либо будут только легкие бомбардировщики и не будет тяжелых.

На материале этой задачи далее будет рассмотрен общий подход к формализации логических задач распознавания и методы их решения.

Основу для постановки логической задачи распознавания составляют два конечных множества Х и L ‚ элементами которых являются двоичные (булевы) логические переменные х_j , l_j:

Х = {х₁‚ х₂‚...‚ х_n }, L = {l₁‚ l₂‚...‚ l_m}.

Одно из них, например Х, является множеством классов‚ другое – L - множеством признаков. Их значения будут:

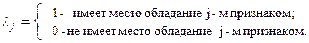
Для нашего примера Х = { х₁‚ х₂‚ х₃ } ‚ L = {l₁‚ l₂} ‚ где булевы переменные означают (равны 1):

х₁ - наличие истребителей сопровождения;

х₂ - наличие истребителей перехватчиков;

х₃ – наличие штурмовиков;

l₁ - наличие тяжелых бомбардировщиков;

l₂ - наличие легких бомбардировщиков.

Как видно‚ в данном случае разница между классами и признаками определяется структурой исходных данных и является весьма условной.

Для конкретной предметной области между логическими переменными х_i (i = 1‚2‚...‚ n) и l_j =(j = 1‚ 2‚...‚ m) устанавливаются зависимости‚ выражающиеся в форме логических условий вида:

х_i = F_i (l₁‚ l₂‚...‚ l_m);

l_j = Ф_j (х₁‚ х₂‚...‚ х_n),

или

х_i ® F_i (l₁‚ l₂‚...‚ l_m) = 1;

Ф_j (х₁‚ х₂‚...‚ х_n) ® l_j = 1,

или

F (х₁‚ х₂‚...‚ х_n) ® Ф (l₁‚ l₂‚...‚ l_m) = 1,

или

F(х₁‚ х₂‚...‚ х_n ‚ l₁‚ l₂‚...‚ l_m) = Ф (х₁‚ х₂‚...‚ х_n, l₁‚ l₂‚...‚ l_m).

Подобные зависимости выражают формально априорную информацию для задач распознавания‚ которая в общем случае в результате преобразований может быть представлена единым соотношением вида

Y (х₁‚ х₂‚...‚ х_n‚ l₁‚ l₂‚...‚ l_m) = 1 (3.1)

Приведение к форме (3.1) возможно на основе известных преобразований, например:

зависимость F(х₁‚ х₂‚...‚ х_n‚ l₁‚ l₂‚...‚ l_m) = Ф (х₁‚ х₂‚...‚ х_n‚ l₁‚ l₂‚...‚ l_m)

эквивалентна выражению F() ~ Ф() = 1 = [ F() & Ф() ]Ú [ F() &Ф()],

а зависимость F(х₁‚ х₂‚...‚ х_n‚ l₁‚ l₂‚...‚ l_m) ® Ф(х₁‚ х₂‚...‚ х_n‚ l₁‚ l₂‚...‚ l_m) = 1

эквивалентна F() Ú Ф() = 1.

В нашем конкретном примере априорная информация может быть представлена в форме

Y (х₁‚ х₂‚ х₃‚ l₁‚ l₂) = х₁· х₂ · х₃ · l₁ Ú х₁·х ₂·l₁ (х₃·l₂ Ú х₃·l₂) = 1, (3.2)

устанавливающей “истинность” перечисленных выше условий‚ регламентирующих состав боевых средств при налете противника.

Задача распознавания возникает‚ когда в дополнение к априорной информации (3.1) появляется полученная на основе дополнительных наблюдений (экспериментов) апостериорная информация ‚ устанавливающая “истинность” некоторой заданной булевой функции G(l₁‚ l₂‚...‚ l_m) логических переменных l₁‚ l₂‚...‚ l_m и требуется определить‚ какие выводы можно сделать относительно логических переменных х₁‚ х₂‚...‚ х_n и выражающей их состояние и взаимосвязь функции F(х₁‚ х₂‚...‚ х_n).

Формально это сводится к нахождению булевой функции F(х₁‚ х₂‚...‚ х_n)‚ такой, чтобы выполнялось условие

G (l₁‚ l₂‚...‚ l_m) ® F (х₁‚ х₂‚...‚ х_n) = 1 (3.3)

при ограничениях (3.1). Эта задача называется прямой задачей распознавания.

Если же апостериорная информация задана в виде булевой функции R (х₁‚ х₂‚...‚ х_n) переменных х₁‚ х₂‚...‚ х_n и нужно определить‚ какие следствия это породит в отношении переменных l₁‚ l₂‚...‚ l_m ‚ т.е. найти функцию Q (l₁‚ l₂‚...‚ l_m) ‚ удовлетворяющую уравнению

R (х₁‚ х₂‚...‚ х_n) ® Q (l₁‚ l₂‚...‚ l_m) =1 (3.4)

при ограничениях (3.1)‚ то такая задача называется сопряженной задачей распознавания.

Принципиальная разница между прямой и сопряженной задачами распознавания состоит в том‚ что в первом случае апостериорная информация, образующая “посылку”, задается на множестве признаков L‚ а искомое “следствие” определяется на множестве классов Х‚ тогда‚ как во втором случае наоборот. Однако в обоих случаях требуется на основании заданной “посылки” определить “следствие”‚ удовлетворяющее априорной информации (3.1).

Применительно к рассматриваемому примеру апостериорная информация в п. а) формально задается в виде

R(х₁‚ х₂‚ х₃) = x_{1 ·} х₃

и ставится сопряженная задача распознавания:

(x_{1 ·} х ₃) ® Q (l₁‚ l₂) = 1, Q (l₁‚ l₂) =?.

В п. б) апостериорная информация задается в виде

G (l₁‚ l₂) = (l₁ Ú l₂) Ú l_{1 ·} l₂ = l_{1 ·} l₂ Ú l_{1 ·} l₂ = l₁

и ставится прямая задача распознавания:

l₁ ® F (х₁‚ х₂‚ х₃) = 1, F (х₁‚ х₂‚ х₃) =?

Наряду с прямой и сопряженной задачами распознавания могут существовать и обратные, когда апостериорная информация задает «следствие», а необходимо определить «посылку», которая это следствие порождает и удовлетворяет априорной информации (3.1).

Так если задана Q (x_1, х₂‚ …, х_n) и требуется найти R (l₁‚ l₂, …, l_m) такую, что

R (l₁‚ l₂, …, l_m) ® Q (x_1, х₂‚ … х_n) = 1, R (l₁‚ l₂, …, l_m) =?, (3.5)

то это обратная прямой задача распознавания.

Если же задана H (l₁‚ l₂, …, l_m) и требуется найти L(х₁‚ х₂‚ …, х_n), такую, что

L (х₁‚ х₂‚ …, х_n) ® H (l₁‚ l₂, …, l_m) = 1, L (х₁‚ х₂‚ …, х_n) =?, (3.6)

то это обратная сопряженной задача распознавания.

Например:

в) Какая ситуация с участием в налете тяжелых и легких бомбардировщиков влечет за собой наличие истребителей сопровождения и отсутствие штурмовиков (обратная прямой задача распознавания)?

R (l₁‚ l₂) ® x₁ х ₃ = 1, R (l₁‚ l₂) =?

г) Какая ситуация с участием в налете истребителей и штурмовиков влечет за собой наличие легких бомбардировщиков и отсутствие тяжелых (обратная сопряженной задача распознавания)?

L (х₁‚ х₂‚ х₃) ® l_{1 ·} l₂ = 1, L (х₁‚ х₂‚ х₃) =?

Метод решения логических задач распознавания

Принципиальная возможность решения поставленных логических задач распознавания связана с существованием логической зависимости между классами и признаками‚ которая содержится в априорной информации (3.1).

Представление этой зависимости в более явной форме в виде соотношения между наборами (х₁‚ х₂‚...‚ х_n) и (l₁‚ l₂‚...‚ l_m) ‚ удовлетворяющего (3.1)‚ лежит в основе метода и связана с построением так называемого сокращенного базиса.

Пусть определена функция Y(х₁‚ х₂‚...‚ х_n‚ l₁‚ l₂‚...‚ l_m), выражающая априорную информацию в соотношении (3.1).

Сокращенный базис есть множество (n+m) разрядных наборов ‚ при которых удовлетворяется условие (3.1), то есть множество наборов (х₁‚ х₂‚...‚ х_n‚ l₁‚ l₂‚...‚ l_m) на которых функция y () равна единице (множество T₁ ^y функции y). Сокращенный базис для заданной функции y может быть представлен в виде‚ например‚ специальной таблицы (см. таблицу 3.1).

Таблица 3.1

х1			· · ·
х2
· · ·
хn
l1
l2
· · ·
lm			· · ·

Каждый элемент сокращенного базиса - (n+m) - разрядный двоичный набор (столбец в таблице 3.1)‚ может быть разбит на две части: n - разрядный‚ соответствующий аргументам х₁‚ х₂‚...‚ х_n (верхняя часть таблицы) и m -разрядный‚ соответствующий аргументам l₁‚ l₂‚...‚ l_m (нижняя часть таблицы). Таким образом устанавливается соответствие между наборами (х₁‚ х₂‚...‚ х_n) и наборами (l₁‚ l₂‚...‚ l_m) ‚ при которых априорная информация является “истинной”, (выполняется (3.1)).

Такое соответствие между наборами можно формализовать с помощью булевой матрицы Е размера 2 ⁿ ×2 ^m ‚ элементы которой e_ij = 1‚ если i -ый набор (х₁‚ х₂‚...‚ х_n) совместно с j -м набором (l₁‚ l₂‚...‚ l_m) образуют элемент множества T ₁^y , и e_ij = 0 в противном случае. Назовем такую матрицу перестановочной.

Продемонстрируем построение сокращенного базиса для априорной информации‚ представленной в соответствии с выражением (3.2). Составим для его правой части

Y (х₁‚ х₂‚ х₃‚ l₁‚ l₂) = х₁· х₂ · х₃ · l₁ Ú х₁·х ₂·l₁ (х₃·l₂ Ú х₃·l₂)

таблицу истинности (табл. 3.2) и по ней найдем сокращенный базис (табл. 3.3).

Таблица 3.2

T

x1

x2

x3

λ1

λ2

__ __ x1·x2·x3 · λ 1

__ x1·x2·x3 · λ 1· λ 2

__ __ __ x1·x2·x3 ·λ1·λ2

ψ(x1,x2,x3, λ 1, λ 2)

Таблица 3.3

T
х1
х2
х3
l1
l2
j

Как видно‚ сокращенный базис состоит из четырех 5-ти разрядных наборов (12‚ 13‚ 18 и 23) и регламентирует следующую связь между наборами (х₁‚ х₂‚ х₃) с номерами i и наборами (l_1‚ l₂) с номерами j:

i = 3 ® j = 0, i = 3 ® j = 1, i = 4 ® j = 2, i = 5 ® j = 3.

Соответствующая перестановочная матрица имеет вид (рис. 3.1).

=

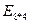Рис. 3.1

После того‚ как определены искомые связи между наборами (х₁‚х₂‚...‚ х_n) и (l_1‚ l_2‚...‚ l_m) прямая и сопряженная задачи распознавания решаются путем удовлетворения соотношениям (3.3) или (3.4) наборами с номерами i и j ‚ находящимися в такой связи. Практически это осуществляется путем “вычисления” изображающего числа искомой ФАЛ на основе логического умножения справа изображающего числа ФАЛ‚ задающей апостериорную информацию, на перестановочную матрицу‚ отображающую априорную информацию.

Для прямой задачи распознавания (3.3) это имеет вид:

#F (х₁‚ х₂‚...‚ х_n) = #G (l_1‚ l_2‚...‚ l_k) ÄE^Т (3.7)

(1× 2 ^m) (1× 2 ^m) (2 ^m ×2 ⁿ)

Для сопряженной задачи распознавания (3.4):

#Q (l_1‚ l_2‚...‚ l_m) = #R (х₁‚ х₂‚...‚ х_n) Ä E (3.8)

(1× 2 ^m) (1× 2 ⁿ) (2 ⁿ ×2 ^m)

Обоснованием данного способа “вычисления” искомых ФАЛ может служить известное свойство‚ проявляющееся при умножении справа изображающего числа ФАЛ‚ отличной от константы «ноль»‚ например‚ R(х₁‚ х₂‚...‚ х_n) ‚ на прямоугольную булеву матрицу‚ например Е‚ и заключающееся в том‚ что единица в i-ой строке и j-м столбце матрицы Е (то есть е_ij = 1) обеспечивает перемещение единицы‚ находящейся на i -ом месте в #R (х₁‚ х₂‚...‚ х_n) на j -ое место результата - изображающего числа #Q (l_1‚ l_2‚...‚ l_m).

Это значит‚что при е_ij = 1 единица на i -ом месте #R (х₁‚ х₂‚...‚ х_n) обеспечивает единицу на j -ом месте # Q (l_1‚ l_2‚...‚ l_m) (см. рис 3.2)‚ что соответствует истинности импликации. Если учесть все единицы в #R (х₁‚ х₂‚...‚ х_n) ‚ то #R (х₁‚ х₂‚...‚ х_n) ® #Q (l_1‚ l_2‚...‚ l_k) = 1‚ что соответствует решению задачи (3.4).

Аналогично при умножении #G (l₁‚ l₂‚...‚ l_m) на Е^Т получаем #F (х₁‚ х₂‚...‚ х_n)‚ причем #G (l₁‚ l₂‚...‚ l_m) ® #F (х₁‚ х₂‚...‚ х_n) = 1.

Рис. 3.2

Применяя описанный метод к решению конкретных задач распознавания а) и б) для рассматриваемого примера, находим:

а) #R (х₁‚ х₂‚ х₃) = # (х₁ · х₃) = (00001010),

#Q (l_1‚ l₂) = (00001010) Ä = (0010),

следовательно Q(l_1‚ l₂) = l₁·l₂, что обозначает: в налете будут участвовать тяжелые бомбардировщики и не будет легких;

б) #G (l_1‚ l₂) = # (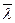 ₁) = (1100),

#F (х₁‚ х₂‚ х₃) = (1101) Ä = (00010000),

следовательно F (х₁‚ х₂‚ х₃) = x_{1 ·} х_{2 ·} х₃, что означает: в налете будут участвовать истребители-перехватчики и штурмовики и не будет истребителей сопровождения.

Решение обратных задач распознавания может быть осуществлено путем сведения их к прямым путем элементарных преобразований.

Пусть для заданной функции Q (х₁‚ х₂‚...‚ х_n) требуется найти такую функцию R(l₁‚ l₂‚...‚ l_m) =?‚ что R (l₁‚ l₂, …, l_m ® Q (x_1, х₂‚ … х_n) = 1.

Так как R ® Q = R Ú Q = Q Ú R = Q ® R = 1‚ то рассматриваемая обратная задача может быть заменена прямой

Q (x_1, х₂‚ … х_n) ® R (l_1‚ l_2‚... l_k) = 1, R (l₁‚ l₂, …, l_k) =?,

содержащей инверсии заданной и искомой функции.

На этом построение методики решения задач распознавания (3.3)‚ (3.4)‚ (3.5)‚ (3.6) завершено.

В заключение‚ рассмотрим важный частный случай.

Пусть сокращенный базис состоит из 2 ^m (n + m) - разрядных наборов‚ причем в нем представлены все m - разрядные наборы l₁‚ l₂‚...‚ l_m (такая ситуация имела место в нашем примере и отражена в таблице 3.3). Соответствующая перестановочная матрица Е имеет по одной единице в каждом столбце. Можно заметить‚ что в этом случае логические переменные х₁‚ х₂‚...‚ х_n могут быть представлены‚ как некоторые функции логических переменных l₁‚ l₂‚...‚ l_m ‚, образующие решение булевского уравнения (3.1) в виде

х_i = f_i (l₁‚ l₂‚...‚ l_m) ‚ i = 1‚2,..., n. (3.9)

Например‚ таблица 3.3 задает три ФАЛ:

х ₁ = l₁, х ₂ = l₁, х₃ = l₁ Ú l₂.

В данной ситуации решение сопряженной задачи распознавания (3.4) может быть получено аналитически путем подстановки в заданную функцию R(х₁‚ х₂‚...‚ х_n) функций х_i = f_i (l₁‚ l₂‚...‚ l_m). В результате получится искомая функция Q (l₁‚ l₂‚...‚ l_m).

Для рассматриваемого примера R (х₁‚ х₂‚ х₃) = х₁ · х ₃

Q (l_1‚ l₂) = R (f₁ (l_1‚ l₂)‚ f₂ (l_1‚ l₂)‚ f₃ (l_1‚ l₂)) = l₁· (l₁ Ú l₂) = l₁· l₁· l₂ = ₌ l₁ · l₂,

что совпадает с полученными ранее.

При наличии нескольких единиц в каждом столбце сокращенного базиса решение исходного уравнения вида (3.9) будет не единственное. При отсутствии единицы хотя бы в одном столбце решения уравнения (3.1) в виде х_i = f_i (l₁‚ l₂‚...‚ l_m) ‚ i = 1‚2,..., n не существует.

Следует заметить, что рассмотренный выше вариант представления сокращенного базиса в виде перестановочной матрицы соответствует заданию конечного автомата без памяти с двоичными входами l₁‚ l₂‚...‚ l_m и выходами х₁‚ х₂‚...‚ х_n, обеспечивающего решение исходного уравнения (3.1).

Наличие сокращенного базиса позволяет искать решения исходного уравнения (3.1) также в виде

l_j = φ_j (х₁‚ х₂‚...‚ х_n) ‚ j = 1‚2,..., m. (3.10)

Однако вопрос о существовании решений и их количестве в этом случае будет определяться наличием и расположением единиц уже в строках перестановочной матрицы.

В данной лабораторной работе необходимо осуществить анализ полученного сокращенного базиса на существование и единственность решения (3.9). При наличие нескольких привести все решения.

В конкретных приложениях логические задачи распознавания приходится решать при наличии больших массивов данных о классах и признаках объектов‚ поэтому весьма актуальными являются алгоритмизация решений и реализация их на ЭВМ.

Дата добавления: 2017-01-13