Определение гамильтонова пути в графе

Гамильтонов путь в графе – это путь, проходящий через все вершины графа, причем каждая вершина встречается в нем только один раз. Если этот путь замкнут, то говорят о гамильтоновом цикле или контуре.

В качестве примера рассмотрим задачу определения очередности решения на ЭВМ вычислительной программы (алгоритма) А,состоящей из п подпрограмм A_i; i =1,2,…, n, причем на порядок выполнения подпрограмм накладываются ограничения в виде

A_i → A_j, (4.1)

т.е. выполнение подпрограммы A_i предшествует выполнению подпрограммы A _j, i, j Î {1,2,…, n } или

A_i A_j, (4.2)

т.е. порядок выполнения программ A_i и A_j безразличен.

Эту задачу удобно геометрически отобразить в виде графа, где каждой i вершине соответствует A_i - подпрограмма, а связи между подпрограммами соответствуют дугам или ребрам. Причем дуга соответствует связи A_i → A_j, а ребро - связи A_i A_j.

Если предполагается, что программа A будет выполнена, когда выполнены все подпрограммы A_i, i =1,2,…, n (без повторений), то определение очередности выполнения подпрограмм A _iсводится к определению на графе гамильтонова пути. Очевидно, что эту задачу можно решить перебором всех возможных вариантов (n! в насыщенном графе) с одновременной проверкой выполнения всех условий (4.1), (4.2). При n = 2 максимально возможно всего два варианта, при n = 3 - шесть, при n =10 существует более трех с половиной миллионов возможных вариантов, из которых надо выбрать допустимые, удовлетворяющие условиям (4.1), (4.2).

Решение поставленной задачи может быть облегчено, если воспользоваться алгоритмом Фаулкса, позволяющим во многих случаях значительно уменьшить количество рассматриваемых возможных вариантов [1].

Алгоритм Фаулкса. Рассматривается n операций (вершины графа) A_1, A_2,…, A_n, между которыми существуют соотношения:

A_i → A_j , A_i → A_j, i, j Î {1,2,…, n } (4.3)

Задача состоит в том, что среди всех возможных путей найти, если это возможно, путь (или несколько путей), проходящий один и только один раз через каждую извершин графа и удовлетворяющий написанным выше соотношениям (4.3), то есть гамильтонов путь.

Идея вычислений, которые необходимо выполнить при использовании алгоритма Фаулкса, заключается в нахождении матрицы R^N путем последовательногобулевого умножения матрицы R¹ достижимости не более чем за один шаг саму на себя N раз (матрица R¹ может быть получена из матрицы смежности R в результате подстановки единиц на главной диагонали).

Элементы r^N_ij матрицы R ^N, определяются как

Вычисления следует прекратить, если R^N = R^{N -1} .

На каждом цикле вычисления возможны некоторые упрощения матрицы, связанные с выявлением «начальных» и «конечных» вершин, ограничивающих возможность дальнейшего построения ГП из общего множества возможных путей в графе.

Порядок решения задачи:

1. Задаем номер цикла вычислений N= 1.

2. Используя соотношения (4.3), составляем граф, вершины которого есть операции, а направленные дуги графа определяются заданными соотношениями между операциями.

3. Составляем матрицу R¹ графа, элементы r¹_ij которой могут принимать значения 0 либо 1. Если r¹_ij = 1, то это указывает на то, что операция (вершина) A_j должна следовать за операцией (вершиной) A_i. Полученная таким образом матрица R¹ является булевой матрицей (каждый элемент может принимать значения 0 или 1). Она является исходной для всех дальнейших вычислений.

4. Используя матрицу R^N (на первом цикле вычислений R^N = R¹), длякаждой вершины графа (операции) проверяем принадлежность ее кначальной или конечной вершине ГП по следующим правилам.

Вершина (операция) является начальной вершиной ГП, если во всей строке матрицы стоят единицы, а во всем столбце (за исключением их пересечения) - нули. Вершина (операция) является конечной вершиной ГП, то во всей строке матрицы стоят нули (за исключением их пересечения), а во всем столбце - единицы.

5. Упрощаем матрицу R^N графа, вычеркивая из нее строки и столбцы, соответствующие начальной или (и) конечной вершине ГП. Получаем матрицу (R^N)^'.

6. Увеличиваем на единицу номер цикла, т.е. N = N +1.

7. Находим матрицу (R^N)^', выполнив булевое умножение матрицы (R^{N -1})^' на матрицу (R¹)^', которая получается из исходной матрицы R¹ вычеркиванием из нее строк и столбцов, соответствующих начальным и конечным вершинам ГП, найденным во всех предыдущих циклах вычислений. Булевое перемножение матриц производится по обычным правилам умножения, только вместо умножения используется конъюнкция, а вместо сложения – дизъюнкция.

8. Проверяем условие выполнения равенства матриц (R^N)^' и (R^{N -1})^'.

Если это условие выполняется, то переходим к п. 10, Иначе - к п. 9.

9. Проверяем условие равенства всех элементов матрицы R^N единице. Если это условие выполняется, то нет необходимости в дальнейших вычислениях матрицы (R ^N)^', так как очевидно, что (R^{N +1})^'=(R^N)^', переходим к п. 10. Если нет - к п. 4.

10. Составляем матрицу R^b , возвращая в матрицу (R^N)^', строки и столбцы, вычеркнутые в п. 5 во всех циклах вычислений.

11. Составляем матрицу R^c, перегруппировывая одновременно строки и столбцы матрицы R^b таким образом, чтобы все нули были расположены под главной диагональю, а единицы - над ней.

Квадратные матрицы, состоящие из единиц, опирающихся на главную диагональ, образуют классы эквивалентности вершин (совокупности вершин графа, эквивалентных с точки зрения очередности их присутствия в гамильтоновом пути).

Если для данного графа мы получили m классов эквивалентности (m £ n), то есть B₁,…,B_m, и в каждый класс эквивалентности B_d, d = 1,2,…, m входят S_d вершин графа, то можно сказать, что вершины, входящие в класс эквивалентности B_d, расположенные выше и левее класса эквивалентности B_l в матрице R^c будут предшествовать в Гамильтоновом пути вершинам из класса эквивалентности B_l.

Нахождение Гамильтоновых путей в этом случае значительно упрощается. В соответствии с классами эквивалентности мы получили упорядоченные группы вершин. В качестве начальной выбирается вершина из первого класса эквивалентности. Если их в нем несколько, то следующая выбирается из этого же класса и так до тех пор, пока не будут исчерпаны все вершины этого класса. Затем переходим к вершинам следующего класса и т.д. пока не будут использованы все вершины графа и построен ГП. Следует заметить, что при выборе очередной вершины необходимо обязательно проверять выполнение условий (4.3). Если условия не выполняются, очередность следования вершин из одного класса эквивалентности меняется. Максимальное число возможных вариантов сокращается до произведения B ₁ ! ∙ B ₂ ! ∙, …, ∙ B_m!

Пример. Пусть программа A состоит из 6 операций (подпрограмм) A _1, A _2,…, A ₆, между которыми существуют следующие соотношения:

A ₁ → A ₂ , A ₂ → A ₃ , A ₃ → A ₄ , A ₅ → A ₂ , A ₆ → A ₂ ,

A ₁ → A ₄, A ₂ → A ₄, A ₅ → A ₄ , A ₆ → A ₄ ,

A ₁ → A ₆, A ₂ → A ₅ , A ₆ → A ₅

A ₂ → A ₆ . (4.4)

Цель задачи состоит в нахождении пути, проходящего только один раз через все операции (вершины графа) и удовлетворяющего написанным соотношениям. Без учета ограничений (4.4) всего возможно 6! = 720 вариантов следования вершин.

Для решения задачи воспользуемся приведенным алгоритмом.

1. Зададим номер цикла N = 1.

2. Составим граф (рис. 4.1), соответствующий соотношениям (4.4).

Рис. 4.1

3. Составим матрицу R ¹ достижимости не более чем за один шаг.

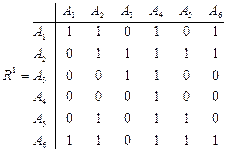
4. Проверим матрицу R ¹ на наличие начальной или конечной вершин в графе.

Очевидно, что A ₄ есть конечная вершина каждого гамильтонова пути, поскольку никакая дуга не имеет эту вершину своим началом, тогда как дуга, исходящая из любой другой вершины, достигает вершину A _4. Это свойство выражается наличием единиц во всем столбце A ₄ и нулей во всей строке A ₄ (за исключением их пересечения).

5. Вычеркиваем столбец и строку A ₄. Получаем матрицу (R ¹)^' .

6. N =1+1=2.

7. Произведем булевое умножение матриц) (R ¹)^' Ä (R ¹)^' = (R ²)^'.

Наличие 1 в матрице означает существование между соответствующими вершинами путей длиной меньшей или равной двум, а 0 - их отсутствие.

8. Проверяем условие равенства (R ²) ^' и (R ¹)^' . Так как они не равны, переходим к п. 9.

9. Проверяем условие равенства всех элементов матрицы единице. Так как оно не выполняется, то возвращаемся к п.4.

4. Рассмотрим матрицу (R ²) ^' .

Вершина A ₃ , является конечной вершиной гамильтонова пути на данном цикле вычислений.

5. Вычеркиваем столбец и строку A ₃. Оставшаяся матрица имеет вид

(R ²) ^' = .

6. N =2+1=3.

7. Производим умножение (R ² )^'Ä (R ^' ) = (R ³ )^'.

(R ³) ^' = .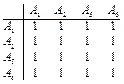

8. (R ³) ^' ¹ (R ² ) ^'

9. Все элементы (R ^N) ^', равны единице. Очевидно, что матрицы (R ⁴) ^', (R ⁵) ^' и т.д. также будут равны, т.к. будут иметь все элементы, равные единице.

Переходим к п.10.

10. Матрицу R ^b получаем возвращением строк и столбцов, вычеркнутых в п. 5.

11. Перегруппируем строки и столбцы матрицы R ^bтак, чтобы все нули были расположены под главной диагональю, а единицы - над ней: Получаем матрицу R ^c

Таким образом, получили три класса эквивалентности:,

- в первый класс входят вершины A ₁, A ₂, A ₅, A ₆;

- во второй - вершина A ₃;

- в третий - вершина A _4.

Т.е. в гамильтоновом пути вершины A ₁, A ₂, A ₅, A ₆ предшествуют вершине A ₃, которая, в свою очередь, предшествует вершине A ₄. Всего возможно 4! ∙ 1! ∙ 1! = 24 вариантов следования вершин.

С учетом необходимости выполнения условий (4.4) определение гамильтонова пути становится достаточно простым делом. В данном примере получим единственный ГП: A ₁, A ₆, A ₅, A ₂, A ₃, A ₄.

Алгоритм Фаулкса в общем случае не решает однозначно задачу определения Гамильтонова пути, он только частично упорядочивает множество вершин, снижая тем самым размерность решаемой задачи. В случае, когда в каждый класс эквивалентности входит только одна вершина, алгоритм Фаулкса определяет гамильтонов путь однозначно.

Дата добавления: 2017-01-13