Определение связности графа

Неориентированный граф называется связным, если для любой пары вершин х_i,х_jÎX существует хотя бы один маршрут, их соединяющий. В противном случае граф несвязан. Несвязный граф может быть единственным образом разбит на группы взаимосвязанных вершин (на связные компоненты) таким образом, что не существует маршрута, соединяющей какие-либо из вершин различных компонент.

Решим задачу определения связности графа с помощью элементов алгоритма Фаулкса.

Пусть дана матрица смежности R неориентированного графа G (матрица R симметрична относительно главной диагонали), имеющего n вершин. Необходимо определить, является ли этот граф связным. В случае, если граф несвязный, то требуется выделить из него все т связных подграфов G _1, G _2,…, G _m таких, что, например, из любой вершины подграфа G ₁ можно найти путь или маршрут, ведущий к любой другой вершине этого же подграфа, но нельзя найти путь или маршрут ни к одной вершине, не принадлежащей данному подграфу G ₁. Требуется определить, какие вершины входят в каждый из подграфов.

На основании матрицы смежности R получим матрицу достижимости не более чем за один шаг R ¹.

Затем, в соответствии с алгоритмом Фаулкса, найдем матрицу R^N путем булевского перемножения матриц (R^N = R^{N -1} Ä R ¹ ) до тех пор, пока не достигнем R^N = R^{N -1}. Полученная матрица R^N является матрицей достижимости графа G. Она позволяет выявить связные подграфы и номера вершин, входящих в связные подграфы. Для этого необходимо в некоторой i - строке матрицы R^N найти элементы r^N_ij = 1, i, j = 1,…, n. Номера столбцов j, где r_ij = 1, и будут номерами вершин, входящих в связный подграф, включающий в себя i -ю вершину. Рассматривая последовательно все несовпадающие строки матрицы можно выявить все т связных подграфов исходного графа G.

В случае ориентированного графа, для решения задачи выделения связных подграфов, не связных между собой путем или маршрутом, необходимо перейти от ориентированного графа к неориентированному, заменив дуги неориентированными ребрами (звеньями). При возникновении параллельных звеньев оставить для дальнейшего рассмотрения только по одному звену, связывающему соответствующие вершины. В остальном процесс поиска связных подграфов не меняется.

Пример.

Пусть задана матрица R ¹ достижимости не более чем за один шаг неориентированного графа G, имеющего n = 8 вершин.

Необходимо проверить граф на связность и выявить все связные подграфы.

1. Зададим начальный номер цикла вычислений: N = 1.

2. N= N +1 =2.

3. Производим умножение R ¹ Ä R ¹ = R ²

.

4. Проверяем условие равенства R ² и R ¹. Они не равны. Переходим к п. 2.

2) N = 2 + 1 = 3.

3) Умножение R ² Ä R ¹ = R ³.

.

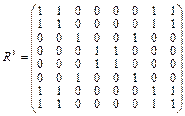4) Проверяем условие равенства матриц R ² и R ³. Так как они равны, то это означает, что путь длиной 2 - максимальный в данной графе, и дальнейшее перемножение матрицы не имеет смысла, так как мы будем получать одну и ту же матрицу. Найденная матрица R ³ есть матрица достижимости исходного графа. Наличие нулей в полученной матрице показывает, что между соответствующими элементами отсутствует путь любойдлины и,следовательно, данный граф — несвязный.

5. Выбираем начальную вершину для выявления связных подграфов: i =1.

6. В строке i =1 выбираем все элементы r ³_{1 j} , равные единице (j =1,…, n). r ³₁₁ = r ³₁₂ = r ³₁₇ = r ³₁₈ = 1. Номера столбцов, в которых r ³ _ij = 1 - это номера вершин первого связного подграфа, входящего в данный граф. То есть вершины 1, 2, 7, 8 образуют связный подграф G ₁ .

7. Определяем номер очередной вершины i = 1 + 1 = 2. Так как 2 ≤ 8, то на 8 (иначе на 9).

8. Проверим – входит ли данная вершина в найденные связные подграфы. Если среди вершин найденных связных подграфов есть данная вершина, то на 7, иначе на 6.

Так как среди вершин связного подграфа G ₁ есть вершина j =2, то возвращаемся к п.7.

7) i = 2 + 1 = 3. Так как 3 ≤ 8, то на 8.

8) Среди вершин связного графа G ₁ нет вершины j =3. Возвращаемся к п. 6.

6.) В строке 3 выбираем элементы, равные единице: r ³₃₃ = r ³₃₆ = 1. Следовательно, во второй связный подграф G ₂ входят вершины 3, 6.

7) Определяем номер очередной вершины i = 3 + 1 = 4. Так как 4 ≤ 8, то на 8.

8.) Среди вершин связных подграфов G ₁ и G ₂ нет вершины j = 4. Возвращаемся к п. 6.

6.) В строке 4 выбираем элементы, равные единице. r ³₄₄ = r ³₄₅ = 1. Следовательно, в третий связный подграф G ₃ входят вершины 4, 5.

7) i = 4 + 1 = 5. Так как 4 ≤ 8, то на 8.

8) Среди вершин связных графов G _1, G _2, G ₃ есть вершина j = 5. Переходим к п.7.

Аналогично проверяются вершины j = 6, 7, 8. Они входят в уже полученные выше подграфы.

9. Если проверены все вершины, то все связные подграфы найдены. Конец.

Таким образом в результате работы алгоритма найдены три связных подграфа:

G ₁ = {1, 2, 7, 8}; G ₂ = {3, 6}; G ₃ = {4, 5} (см. рисунок 4.2)

.

Рис 4. 2.

Дата добавления: 2017-01-13