Интегралдау ќадамдарын тањдау. 1 страница

Берілген интегралды сандыќ єдістердіњ ќайсысымен болса да шешу уаќытында берілген дєлдікті ќамтамасыз ететін ќадам тањдау керек. Кейде интегралдау аралыѓын бірнеше бµлікке бµлу барысында дµњгелектеу, есептеу ќателіктері µсуі м‰мкін. М±ндай ыњѓайсыздыќќа ±шырамас ‰шін интегралдау ќадамын д±рыс тањдау керек. Практикада интегралдау ќадамын 2 тєсілмен тањдайды:

1. Ќалдыќ м‰шені баѓалау арќылы
2. Екілік есептеу арќылы.

1-тєсілде берілген интегралды шешуге тиімді бір сандыќ єдісті тањдап алып, сол єдістіњ ќалдыќ м‰шесініњ формуласын

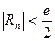(5.13)

баѓалау арќылы h –ты аныќтайды.

Мысалы:

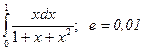
Трапеция єдісін тањдайыќ. Ол єдістіњ ќалдыќ м‰шесініњ формуласы:

.

;

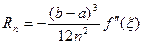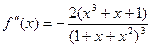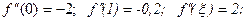
Табылѓан мєндерді 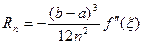формуласына ќойып (5.13)-баѓалауды баќылаймыз, сонда 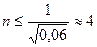екендігі табылады. Енді ќадамды табуѓа болады: 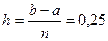. Трапеция формуласына ќойсаќ: .

2-тєсілде берілген интеграл h ќадаммен аралыќты n рет бµледі жєне 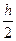ќадаммен аралыќты 2n рет бµледі де екі рет есептеледі. алынѓан интегралдарды сєйкесінше жєне 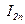деп белгілесек, шарты орындалса, онда 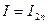деп есептеуге болады, м±ндаѓы I – интегралдыњ дєл мєні. Егер б±л шарт орындалмаса, онда ќадамды таѓы да 2-ге кішірейтеді.

Интегралдау ќадамы берілмеген есептерде, алѓашќы ќадамды 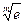санына жуыќ сан ретінде алуѓа болады, м±ндаѓы m=2 трапеция формуласы ‰шін, m=4 – Симпсон формуласы ‰шін. Б±л тєсіл есепті ЭЕМ кµмегімен шешу кезінде ќадамды автоматты т‰рде компьютер тањдайтындай жаѓдай тудырады жєне бірмезгілде есептеу ќадамдары да баќыланып отырады.

Бақылау сұрақтары:

1. Канторовичтің интеграл астындағы функцияның ерекшелігін айшыќтау әдісі?

2. Дәрежелік ќатарлар кµмегімен интегралдау єдісі?

3. Гаусстыњ квадратуралыќ формулалары?

4. Интегралдау ќадамдарын тањдау қалай жүзеге асады?

Тақырыбы: Монте-Карло әдісімен еселі интегралды есептеу

Мақсаты: Интегралдап жуықтап есептеу есептерін шығаруды үйрену

Тапсырма:

E=10^-5 дєлдікпен тµмендегі интегралдарды сєйкес єдісті тањдау арќылы есептеңіздер.

1. ;

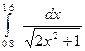2.

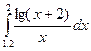
3.

4.

5.

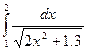
6.

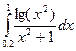
7.

8.

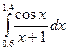
9.

10.

11.

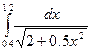
12.

13.

14.

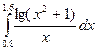
15. , аралыќты 2-ге бµлу арќылы есептеу.

16.

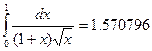
17.

18.

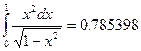
19.

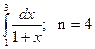
20.

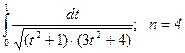
Тапсырманы орындауға әдістемелік нұсқаулар:

Сандық интегралдау есебі

Сандық интегралдау инженерлік және ғылыми деректерді анализдеу немесе сараптау үшін қажетті. Интегралды классикалық әдістермен аналитикалық түрде алу мүмкін болмаған жағдайларда сандық интегралдау есебі қойылады. Кейде интеграл астындағы функция өте күрделі, кейде функцияның кесте лық мәндері ғана берілуі мүмкін.

Сандық интегралдауды сандық квадратура деп те атайды. Ал қолданылатын формулалар квадратуралық формулалар деп аталады.

Сандық интегралдау да дәл және жуықтау болып екіге бөлінеді.

Егер абсцисса өсі бойынан алынатын нүктелер бірқалыпты орналасатын болса, онда Ньютон – Котестің дәл квадратуралық формулалары қолданылады, басқа жағдайда жуықтау – Гаусс формулалары қолданылады.

Сандық интегралдаудың негізгі идеясы - интеграл астындағы функцияны [a,b] аралығында интерполяциялық полиномға жіктеу және полиномның әр мүшесін интегралдау арқылы есептеу процесін жеңілдету.

Интегралдың қателігін төмендету үшін интеграл астындағы функция анықталған [a,b] аралығы h қадаммен бірнеше аралыққа бөлу керек: x_i+1-x_i=h, i=1,2,…,n-1. Қадам тұрақты болған жағдайды қарастырайық.

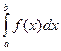(5.1)

түрдегі интеграл берілсін. Дәл әдістерге Ньютон-Котес квадратуралық формулалары жататыны жоғарыда айтылған.

Трапеция әдісі

Егер n=1 болса квадратуралық формула трапеция әдісі деп аталады. Әдіс бойынша; интегралдық қисық пен ох өсі аралығындағы фигура ауданын табу үшін сол фигураны трапециямен толықтырып, ауданын табуға болады:

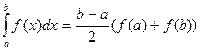(5.2)

Қателікті азайту үшін аралықты бірнеше бөлікке бөліп әр трапецияның ауданын тауып барлығының қосындысы берілген интегралдың мәні деуге болады:

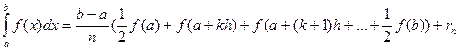(5.3)

Мұндағы

, (5.4)

.

(5.4)-формула әдістің қателігін бағалау формуласы деп аталады. Геометриялық мағынасы трапециямен толықтырылған уақытта осы облысқа кірмей қалған аймақтардың қосындысы, кейде оны қиылу қателігі де дейді. Оның мәні өте аз шама болуы керек.

1-мысал:

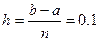
(5.3)- формулаға қоямыз:

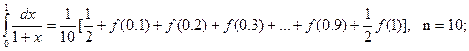
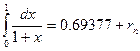
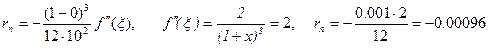
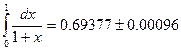
Симпсон әдісі.

N=2 болса Ньютон – Котес формуласы Симпсон єдісін аныќтайды. [a,b] аралыѓын екі симметриялы бµлікке бµледі: 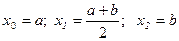н‰ктелері болса, аралыќ ж±п болады, есептеу формуласы:

(5.5)

Онда есептеу ќателігі 16-ѓа азаяды. Ал бµлу аралыѓы таќ болса, онда [a,b] аралыќтыњ алѓашќы ‰ш бµлігінен ‰шінші дєрежелі парабола ж‰ргізнміз, б±л жаѓдайда Симпсоннныњ ‰штен сегіздік формуласы ќолданылады:

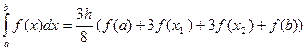
Мысал:

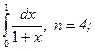
a=0; h=0.25; b=1;

.

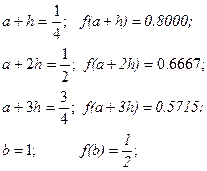
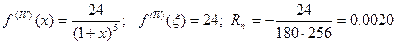Тіктөртбұрыштар әдісі.

[a,b] аралығынан х₀ бір түйін алатын болсақ, чғни f(x)=const болады, онда қарастырып отырған аралықта 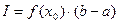деуге болады. Х₀ нүктесін аралықтың тура ортаңғы нүктесі деп алсақ формуласы шығады, оны тіктөртбұрыштар формуласы дейді, әдістің қателігін азайту мақсатында аралықты бірнеше бөлікке бөліп, әр аралықты тіктөртбұрышпен толтырып, ауданын тауып, барлық аудандарды бір біріне қосады:

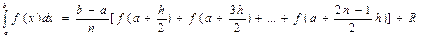(5.6)

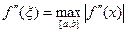
Мысалы:

Табылған мәндерді (5.6)-формулаға қойсақ:

Жоғарыда келтірілген мысалдармен салыстыру арқылы қай әдістің қателігі аз екенін анықтай аласыздар.

Бақылау сұрақтары:

1. Сандық интегралдау есебіне мысал келтіріңіз?

2. Трапеция әдісі қалай жүзеге асады?

3. Симпсон әдісі қалай жүзеге асады?

4. Тіктөртбұрыштар әдісі қалай жүзеге асады?

Тақырыбы: Болжау-түзеу схемасын пайдаланып КДТ сандық шешімін табу.

Мақсаты: Қарапайым дифференциалдық теңдеулерді шешудің бірқадамды сандық әдістерімен есептер шығаруды үйрену

Тапсырма:

Төмендегі қарапайым дифференциалдық теңдеулерді [0.2; 1.2] аралығында 0.1 қадаммен у (0.2)=0.25 бастапқы шартты қанағаттандыратын шешімін Эйлер және Эйлер-Коши әдістерімен тауып, қателіктерін бағалау. Есептеуді үтірден кейін 4 орынмен жүргізу.

№ 1.

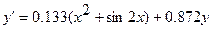
№ 2.

№ 3

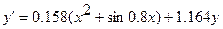
№ 4

№ 5

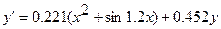
№ 6

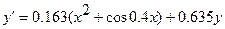
№ 7

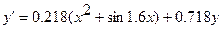
№ 8

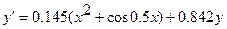
№ 9

№ 10

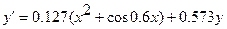
2. Берілген аралықта h=0,2 қадаммен теңдеулерді және теңдеулер жүйелерін Рунге-Кутта әдісімен шешу.

a) 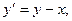y(0)=1.5; a=0; b=1;

b) 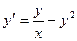, y(1)=1; a=1; b=2;

c) , y(0)=1; z(0)=1; a=0; b=1;

d) 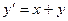, y(0)=1, табу керек y(0.5)

e) , y(0)=1, табу керек y(1)

f) 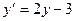, y(0)=1, табу керек y(0.5)

g) 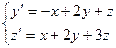y(0)=2, z(0)=-2, x=0.5 болғандағы y,z-тің мәндерін табу керек

i) 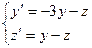y(0)=2, z(0)=-1, x=0.5 болғандағы y,z-тің мәндерін табу керек

3. Рунге-Кутта әдісін қолданып берілген аралықта 10^-4 дәлдікпен төмендегі ҚДТ –ді шешу.

a) , y(0)=1, a=0, b=1

b) 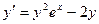, y(0)=1, a=0, b=1

c) , y(1)=0, a=1, b=2

4. Рунге-Кутта әдісін қолданып бастапқы шарты х(0)=0 болғанда төмендегі теңдеулердің шешімдерін анықтау. һ=0,1 болсын.

a) 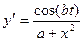, a=1+0.4n, n=0,1,…, 5, b=1+0.8k, k=0,1,2

b) , a=1+0.4n, n=0,1,…, 5, b=1+0.4k, k=0,1,2,3,4,5

c) 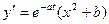, a=1+0.4n, n=0,1,…, 5, b=1+0.4k, k=0,1,2,3,4,5

d) , a=1+0.4n, n=0,1,…, 5

e) 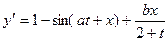, a=1+0.4n, n=0,1,…, 5, b=1+0.8k, k=0,1,2

f) 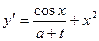, a=1+0.4n, n=0,1,…, 5

g) 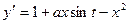, a=1+0.4n, n=0,1,…, 5

5. Рунге-Кутта әдісін қолданып 10^-4 дәлдікке дейін төмендегі теңдеулерді шешу.

a) 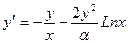, y(1)=1, a=1, b=2,

b) 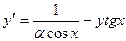, y(0)=1, a=0, b=1,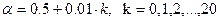

Тапсырманы орындауға әдістемелік нұсқаулар:

Эйлер әдісі

Коши есебін шешудің бұл әдісі бірінші ретті дифференциалдық теңдеуді интегралдауға мүмкіндік береді. Бұл әдістің дәлдігі төмен. Сондықтан практикада көп қолданылмайды. Бірақ бұл әдістің негізінде басқа тиімді, бірақ күрделі әдістерді меңгеру жеңілдейді.

(6.1)-(6.2) Коши есебі берілсін.

Геометриялық мағынасы: һ қадам таңдап алып берілген аралықта бірдей қадаммен нүктелер жиынын құраймыз:

x_i=x₀+ih (i=0,1,2,…). (6.4)

M₀(x₀,y₀) нүктесінен өтетін ізделінді y=y(x) интегралдық қисықты төбелері M_i (x_i,y_i) (i=0,1,2,…) болатын Эйлер сынықтарымен M₀M₁M₂… алмастырылады:

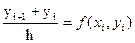(6.5)

Әрбір M_iM_i+1 сынықтары бағыты M_i нүктелерінен өтетін (6.1)-теңдеумен берілген интегралдық қисықтың бағытымен беттеседі.

Сонда есептеу формуласы келесі түрде жазылады:

Y_i+1=y_i+Dy_i, (6.6)

Dy_i=hf(x_i,y_i) (i=0,1,2,…)

Әдіс теңдеулер жүйесіне де қолданылады. Ол 2-мысалмен келтірілген.

1-Мысал:

Эйлер әдісін қолданып [0,1] аралығында h=0,2 қадаммен теңдеуін және у(0)=1 бастапқы шартты қанағаттандыратын мәндер кестесін құру керек болсын.

Есептеу нәтижелері 1-кестеде келтірілген. Кестенің толтырылуы:

Бірінші жолға i=0 болғанда бастапқы мәндер жазылады: x₀=0; y₀=1,0000. Үтірден кейін мәнді цифрларды жоғалтпау үшін 4 орын сақтап отырайық. Осы мәндер және (6)- формула бойынша f(x₀,y₀)=1, сосын , у₁=1+0,2=1,2 мәндері есептеледі.

Екінші жолға i=1 болғанда x₁=0.2, y₁=1.2000 мәндері жазылады. Осы мәндерді қолданып f(x₁,y₁)=0.8667 мәні, мәні есептеледі. Сосын мәнін анықтауға болады. Дәл осылайша i=2,3,4,5 болғандағы есептеулерді анықтауға болады.

Кестенің ең соңғы бағанында салыстыру үшін теңдеудің дәл шешімінің мәндері келтірілген. Кестеден абсолютті қателіктің мәні е=0,0917, салыстырмалы қателігінің 5% екендігі көрінеді.

1-кесте. теңдеуін есептеу алгоритмі.

I	xi	yi	-ді есептеу
	0,2 0,4 0,6 0,8 1,0	1,0000 1,2000 1,3733 1,5294 1,6786 1,8237	0,3333 0,5928 0,7846 0,9532	1,0000 0,8667 0,7805 0,7458 0,7254	0,2000 0,1733 0,1561 0,1492 0,1451	1,0000 1,1832 1,3416 1,4832 1,6124 1,7320

2-мысал:

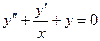
Бастапқы шарттары: .

Аралық [1, 1.5], қадам h=0.1 болсын. Мұндай жағдайда алмастыру қолдану арқылы 1-ретті теңдеулер жүйесін құрып алуға болады:

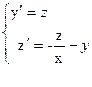және бастапқы шарттары: .

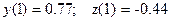Мұндай жүйелер үшін Эйлер формуласы келесі түрде жазылады:

Y_i+1=y_i+hf₁(x_i,y_i,z_i)

z_i+1=z_i+hf₂(x_i,y_i,z_i), i=0,1,2,… (6.7)

(6.7)-ні қолдансақ және f₁(x,y,z)=z; f₂(x,y,z)= 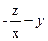болатынын ескерсек:

i=0; x₀=1.00; y₀=0.77; z₀=-0.44; f₁(x₀,y₀,z₀)=-0.44; f₂(x₀,y₀,z₀)= =-0.33;

y₁=y₀+ 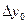=0.726; z₁=z₀+ =-0.473 екендігі шығады. Дәл осылайша келесі мәндерді табу оңайға түседі.

Эйлер – Коши әдісі

Бастапқы нүктедегі ақиқат қисыққа жанама көлбеуі бұрышының тангенсі белгілі және 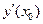-ға тең болса да, ол тәуелсіз айнымалының өзгеруіне байланысты өзгеріп отырады. Сондықтан x₀+h нүктесінде жанама көлбеуі x₀ нүктесіндегі жанама көлбеуіндей болмайды. Осыдан, h интервалында бастапқы жанама көлбеуін сақтай отырып есептеу барысында қателік пайда болады. Эйлер әдісінің дәлдігін арттыру үшін туынды аппроксимациясын жақсарту керек, яғни интервалдың бастапқы және соңғы нүктелерінде туындының орта мәнін алуға болады. Бұл әдісті Эйлер – Коши әдісі дейді. Бұл әдісте алдымен Эйлер формуласы қолданылады:

, i=0,1,2,… Сосын осы мәнді интервал соңындағы 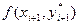туынды мәнін жуықтап есептеуге қолданады. Табылған екі мәннің ортасын анықтап, дәл мәнге өте жуық мән аламыз, бұл формула Эйлер – Коши формуласы деп аталады:

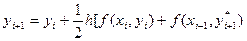(6.8)

Рунге-Кутта әдісі

Бұл әдіс те бірқадамды әдіске жатады.

(6.9)

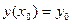(6.10)

(6.9)-теңдеу екі өлшемді қарапайым дифференциалдық теңдеу (ҚДТ) және (6.10)-бастапқы шарт берілсін. [x₀, x_n] аралығында у-тің мәндерін анықтап, функция графигін сызу керек болсын.

нүктелерінде мәндерін Рунге-Кутта формуласымен табамыз:

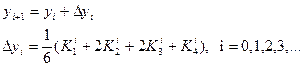
Мұндағы К аралық сандары төмендегідей табылады:

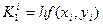
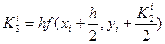
Практикада есептеу қадамдарын 2-кестеге толтырған тиімді.

2-кесте. Рунге-Кутта әдісінің схемасы.

i	X	Y	K=hf(x,y)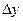
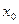
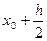
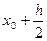
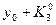
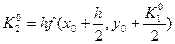
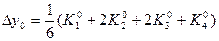
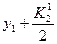
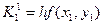
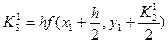
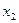
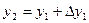
			Т.с.с.

Қадамның дұрыс таңдалуын 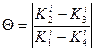бөлшегін есептеу арқылы қадағалауға болады, оның мәні бірнеше жүздіктен аспаса қадам дұрыс таңдалынды, кері жағдайда қадамды кішірейту керек.

Дата добавления: 2017-01-14