
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Интегралдау ќадамдарын тањдау. 2 страница
|
|
|
|
Бұл әдістің дәлдігі 4-ші ретті. Қателігін бағалау өте күрделі, сондықтан екілік есептеу арқылы алынған мәндер бір бірімен салыстырылып, айырмасы дәлдіктен асып кетпеуі тексеріледі, егер айырма мәндері көп ауытқыса, есептеудің келесі қадамындағы х мәнін екі еселенген қадаммен алады, әйтпесе қадамның жартысын алады.
1-мысал: Рунге-Кутта әдісін қолданып  теңдеуін шешу. Бастапқы шарты y(0)=-1, h=0.1, аралық [0,0.5] болсын.
теңдеуін шешу. Бастапқы шарты y(0)=-1, h=0.1, аралық [0,0.5] болсын.
Шешімі:
Есептеу қадамдарын 3-кестеге толтырып отырған дұрыс. Кестені толтыру ережесі:
- 1-ші жолға бастапқы шарт мәндерін жазамыз. Х0=0, у0=-1.
- f(x0, y0)=0.25, K10=0.1*0.25=0.025 мәндерін тауып аламыз.
- 2-ші жолға
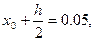
 мәндерін жазамыз.
мәндерін жазамыз. -
 ,
,  мәндерін есептейміз.
мәндерін есептейміз. - 3-ші жолға
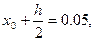
 мәндерін жазамыз.
мәндерін жазамыз. -
 ,
,  мәндерін есептейміз.
мәндерін есептейміз. - 4-ші жолға
 ,
,  мәндерін жазамыз.
мәндерін жазамыз. -
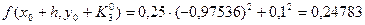 ,
,  мәндерін есептейміз.
мәндерін есептейміз. - 5-ші жолға
 мәнін жазамыз.
мәнін жазамыз. - 6-шы жолға
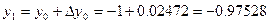
- Осы алгоритмді қайталау арқылы кестенің қалған жолдары толтырылады.
Рунге-Кутта әдісін ҚДТ жүйесіне де қолдануға болады. Егер жүйе жоғарғы ретті болса, теңдеуді 1-ретті түрге келтіріп алу керек.
3-кесте.  теңдеуін шешудің кестелік алгоритмі.
теңдеуін шешудің кестелік алгоритмі.
| i | X | Y | 
| 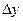
| 
|
| 0.05 0.05 0.1 | -1 -0.98750 -0.98769 -0.97536 | 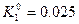
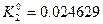

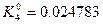
| 
| 0.024 | |
| 0.1 0.15 0.15 0.2 | -0.97528 -0.96289 -0.96257 -0.94987 | 



| 
| 0.025 | |
| 0.2 0.25 0.25 0.3 | -0.94978 -0.93650 -0.93569 -0.92164 | 0.026553 0.028176 0.028138 0.030236 | 0.02824 | 0.023 | |
| 0.3 0.35 0.35 0.4 | -0.92154 -0.90642 -0.90514 -0.88881 | 0.030231 0.032790 0.032732 0.035743 | 0.03284 | 0.023 | |
| 0.4 0.45 0.45 0.5 | -0.88870 -0.87083 -0.86910 -0.84957 | 0.035745 0.039209 0.039134 0.04307 | 0.03925 | 0.022 | |
| 0.5 | -0.84945 |
Бақылау сұрақтары:
1. Эйлер әдісі?
2. Сандық интегралдау есебі дегеніміз не?
|
|
|
3. Эйлер – Коши әдісі?
4. Рунге-Кутта әдісі?
Тақырыбы: Адамс схемасын екі теңдеу жүйесінің сандық шешімін табу Мақсаты: Қарапайым дифференцилдық теңдеулерді шешудің көпқадамды сандық әдістерімен есептер шығаруды үйрену
Тапсырма:
1. Адамс әдісін қолданып 10-2 дәрежесіне дейінгі дәлдікпен төмендегі қарапайым дифференциалдық теңдеулер мен теңдеулер жүйелерін шешу. Бастапқы мәндерді Рунге-Кутта әдісімен есептеу.
a) 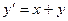 , y(0)=1, табу керек y(0.5)
, y(0)=1, табу керек y(0.5)
b)  , y(0)=1, табу керек y(1)
, y(0)=1, табу керек y(1)
c) 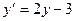 , y(0)=1, табу керек y(0.5)
, y(0)=1, табу керек y(0.5)
d) 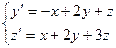 y(0)=2, z(0)=-2, x=0.5 болғандағы y,z-тің мәндерін табу керек
y(0)=2, z(0)=-2, x=0.5 болғандағы y,z-тің мәндерін табу керек
e) 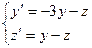 y(0)=2, z(0)=-1, x=0.5 болғандағы y,z-тің мәндерін табу керек
y(0)=2, z(0)=-1, x=0.5 болғандағы y,z-тің мәндерін табу керек
2. Адамс әдісін қолданып берілген аралықта 10-4 дәлдікпен төмендегі ҚДТ –ді шешу. Бастапқы мәндерді Рунге-Кутта әдісімен анықтау.
a)  , y(0)=1, a=0, b=1
, y(0)=1, a=0, b=1
b) 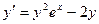 , y(0)=1, a=0, b=1
, y(0)=1, a=0, b=1
c)  , y(1)=0, a=1, b=2
, y(1)=0, a=1, b=2
3. Адамс әдісін қолданып бастапқы шарты х(0)=0 болғанда төмендегі теңдеулердің шешімдердің мәндер кесте сын екі қадамға жалғастыру. һ=0,1 болсын. Бастапқы мәндерді Рунге-Кутта әдісімен анықтау.
a) 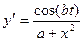 , a=1+0.4n, n=0,1,…, 5, b=1+0.8k, k=0,1,2
, a=1+0.4n, n=0,1,…, 5, b=1+0.8k, k=0,1,2
b)  , a=1+0.4n, n=0,1,…, 5, b=1+0.4k, k=0,1,2,3,4,5
, a=1+0.4n, n=0,1,…, 5, b=1+0.4k, k=0,1,2,3,4,5
c) 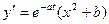 , a=1+0.4n, n=0,1,…, 5, b=1+0.4k, k=0,1,2,3,4,5
, a=1+0.4n, n=0,1,…, 5, b=1+0.4k, k=0,1,2,3,4,5
d)  , a=1+0.4n, n=0,1,…, 5
, a=1+0.4n, n=0,1,…, 5
e) 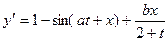 , a=1+0.4n, n=0,1,…, 5, b=1+0.8k, k=0,1,2
, a=1+0.4n, n=0,1,…, 5, b=1+0.8k, k=0,1,2
f) 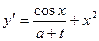 , a=1+0.4n, n=0,1,…, 5
, a=1+0.4n, n=0,1,…, 5
g) 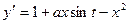 , a=1+0.4n, n=0,1,…, 5
, a=1+0.4n, n=0,1,…, 5
4. Милн әдісін қолданып 10-4 дәлдікке дейін төмендегі теңдеулерді шешу. Бастапқы мәндерді бірқадамды әдістердің біреуімен анықтау.
a) 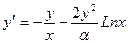 , y(1)=1, a=1, b=2,
, y(1)=1, a=1, b=2, 
b) 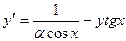 , y(0)=1, a=0, b=1,
, y(0)=1, a=0, b=1, 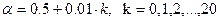
5. Адамс әдісін қолданып 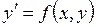 дифференциалдық теңдеудің
дифференциалдық теңдеудің 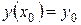 бастапқы шартты қанағаттандыратын шешімдерін
бастапқы шартты қанағаттандыратын шешімдерін 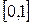 аралығында
аралығында  қадаммен анықтау. Есептеуді төрт ондық таңбамен жүргізу. Бастапқы аралықтағы мәндерді Рунге-Кутта әдісімен анықтау.
қадаммен анықтау. Есептеуді төрт ондық таңбамен жүргізу. Бастапқы аралықтағы мәндерді Рунге-Кутта әдісімен анықтау.
a) 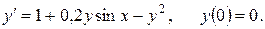
b) 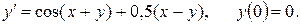
c) 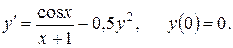
d) 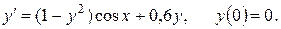
e) 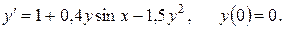
f) 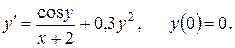
g) 
h) 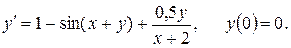
i) 
j) 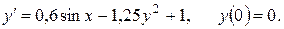
Тапсырманы орындауға әдістемелік нұсқаулар:
|
|
|
 (6.11)
(6.11)
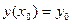 (6.12)
(6.12)
(6.11)-теңдеу екі өлшемді қарапайым дифференциалдық теңдеу (ҚДТ) және (6.12)-бастапқы шарт берілсін. [x0, xn] аралығында у-тің мәндерін анықтап, функция графигін сызу керек болсын. Бұл есепті шешудің көпқадамды әдістері: Адамс және Милн әдістері деп аталады.
Адамс әдісі
Адамс әдісінің идеясы бірқадамды әдіспен табылған мәндер кесте сын толықтыру немесе жалғастыру. Сондықтан есептеің берілгенінде бастапқы шартпен бірге бірнеше нүктедегі функция мәндері табылған болады.
Бастапқы шартты пайдаланып, функция өсімшесінің мәндерін анықтаймыз, оларды qi (i=0,1,2,3) деп белгілейік:

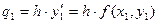
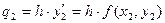

Енді осы мәндердің шектік айырымдарын табамыз:


 ,
, 
Енді функцияның мәндерін есептеу үшін Адамс формуласын қолданамыз. Ол екі түрлі:
- Экстраполяциялық формула:
 ,
,
 ,
,  (6.13)
(6.13)
Бұл формуламен табылған 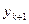 мәндерін алдын ала анықталған функция мәндері деп атаймыз және
мәндерін алдын ала анықталған функция мәндері деп атаймыз және  ,
,  деп белгілейміз. (6.13)-формуламен табылған мәндерді тереңірек анықтау үшін интерполяциялық формуланы қолданамыз.
деп белгілейміз. (6.13)-формуламен табылған мәндерді тереңірек анықтау үшін интерполяциялық формуланы қолданамыз.
- Интерполяциялық формула:
 ,
,
 ,
,  (6.14)
(6.14)
Бұл формуламен табылған 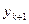 мәндерін жөнделген немесе түзетілген функция мәндері деп атаймыз және
мәндерін жөнделген немесе түзетілген функция мәндері деп атаймыз және  ,
,  деп белгілейміз. Сосын (6.13) және (6.14)-формулалармен алынған мәндерді бір бірімен салыстырамыз. Егер төмендегі шарт орындалса:
деп белгілейміз. Сосын (6.13) және (6.14)-формулалармен алынған мәндерді бір бірімен салыстырамыз. Егер төмендегі шарт орындалса:
 онда әдіс өзінің жалғыз шешіміне жинақталады, орындалмаса – қадамды кішірейтіп есептеуді қайта жүргізу керек.
онда әдіс өзінің жалғыз шешіміне жинақталады, орындалмаса – қадамды кішірейтіп есептеуді қайта жүргізу керек.
Практикада есептеуді жеілдету үшін Адамстың басқа формулалары да қолданылады:
1-формуласы:  ),
), 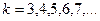 (6.15)
(6.15)
2-формуласы:  ),
), 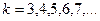 (6.16)
(6.16)
Адамс әдісі дифференциалдық теңдеулер жүйесіне де қолданылады:
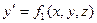
 жүйесі берілсе, оған қолданылатын Адамс формулалары төмендегідей болады:
жүйесі берілсе, оған қолданылатын Адамс формулалары төмендегідей болады:
 (6.17)
(6.17)
 (6.18)
(6.18)
Мұндағы:  ,
,

Милн әдісі.
Бұл әдіс те Адамс әдісі сияқты мәндер кесте сын жалғастыруға мүмкіндік береді. Теңдеу, бастапқы шарт, және қандай да бір әдіспен табылған функцияның бірнеше мәндері берілсін. Функцияның қалған мәндерін анықтау керек.
|
|
|
 (6.19)
(6.19)
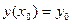 (6.20)
(6.20)
 ,
, 
 мәндерді анықтау үшін Милн формулаларын қолданамыз:
мәндерді анықтау үшін Милн формулаларын қолданамыз:
1. Алдын ала анықтау:  ,
,
- Осы мәндерді қолданып

- Милннің 2-ші формуласымен алдында табылған мәндерді түзетеміз немесе дәлдейміз:
 .
. - Табылған мәндердің қателігін бағалаймыз:
 . Бұл формула есептеудің әр қадамында алынған мәннің дәлдігін тексеріп отырады. Егер дәлдік берілсе және
. Бұл формула есептеудің әр қадамында алынған мәннің дәлдігін тексеріп отырады. Егер дәлдік берілсе және  болса, онда
болса, онда  деп алып yi+1-лерді есептеуге болады, кері жағдайда қадамды кішірейту керек.
деп алып yi+1-лерді есептеуге болады, кері жағдайда қадамды кішірейту керек.
Милн әдісін жүйені шешуге де қолдануға болады. Егер жоғарғы ретті теңдеу берілсе оны 1-ші ретті теңдеуге келтіру керек.
1- мысал: Адамс әдісін қолданып  теңдеуін шешу. Бастапқы шарты y(0)=-1
теңдеуін шешу. Бастапқы шарты y(0)=-1
Шешімі:
(6.15)-(6.16)-формулаларды қолданып есептейік. Рунге-Кутта әдісімен алдын ала бірнеше мәндер табылған болсын.
X1=0.1 y1=-0.97528
X2=0.2 y2=-0.94978
X3=0.3 y3=-0.92154
Есептеу қадамдарын 1-кестеге жазуға болады.
Кестені толтыру ережесіне тоқталайық:
1,2- бағандарға белгілі мәндерді толтырамыз. 3-бағанда уk-дің (k=0,1,2,3)
белгілі мәндерін толтырамыз. Осы мәндерді қолданып,
1-кесте.  теңдеуін шешудің алгоритмі.
теңдеуін шешудің алгоритмі.
| K | xk | yk | Y`k | 
| 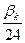
| 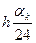
| 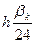
|
| 0.0 | -0 | 0.25 | |||||
| 0.1 | -0.97528 | 0.24779 | |||||
| 0.2 | -0.94978 | 0.26552 | |||||
| 0.3 | -0.92154 | 0.30232 | 0.32834 | 0.32840 | 0.03283 | 0.03284 | |
| 0.4 | -0.88871 | 0.35745 | 0.39237 | 0.39246 | 0.03924 | 0.03925 | |
| -0.88870 | |||||||
| 0.5 | -0.84946 | 0.43040 | |||||
| -0.84946 |
 формуласымен 3-бағандағы сәйкес мәндерді анықтаймыз. 5-6 – бағандардағы
формуласымен 3-бағандағы сәйкес мәндерді анықтаймыз. 5-6 – бағандардағы  белгілеулері (6.15)- (6.16)- формулалардағы жақша ішіндегі қосындыны білдіреді. K=3 болғанда
белгілеулері (6.15)- (6.16)- формулалардағы жақша ішіндегі қосындыны білдіреді. K=3 болғанда  мәнін 5-бағанның сәйкес жолына жазамыз. K=4 болғанда (6.15)-формуламен
мәнін 5-бағанның сәйкес жолына жазамыз. K=4 болғанда (6.15)-формуламен  мәнін тауып, кестеде өз орнына жазамыз. Осы табылған х4, у4 мәндерін қолданып табамыз.
мәнін тауып, кестеде өз орнына жазамыз. Осы табылған х4, у4 мәндерін қолданып табамыз. 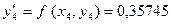 мәнін есептеп өз орнына жазамыз. Әрі қарай K=3 болғанда
мәнін есептеп өз орнына жазамыз. Әрі қарай K=3 болғанда 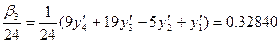 мәнін есептеп өз орнына жазамыз. Енді табылған у4 мәнін (6.16)- формуламен түзетеміз:
мәнін есептеп өз орнына жазамыз. Енді табылған у4 мәнін (6.16)- формуламен түзетеміз:  . Табылған екі мән бір біріне өте жуық болғандықтан кестедегі алдыңғы табылған
. Табылған екі мән бір біріне өте жуық болғандықтан кестедегі алдыңғы табылған  мәнін
мәнін  мәнімен түзетеміз. Осы әдіспен кестенің келесі жолын толтыруға болады.
мәнімен түзетеміз. Осы әдіспен кестенің келесі жолын толтыруға болады.
|
|
|
Бақылау сұрақтары:
1. Қарапайым дифференциалдық теңдеулерді шешудің көпқадамды сандық әдістерін атаңыз?
2. Адамс әдісі?
3. Милн әдісі?
4. Қарапайым екіөлшемді дифференциалдық теңдеу қалай жазылады?
СОӨЖ-НА АРНАЛҒАН ТАПСЫРМАЛАР ЖӘНЕ НҰСҚАУЛАР
СОӨЖ ТАПСЫРМАЛАРЫ:
Тапсырмалар
1-СОӨЖ: «Сызықты емес теңдеулерді және теңдеулер жүйесін шешудің сандық әдістері»
Берілген теңдеулердің түбір жатқан аралығын тауып, жоғарыда келтірілген сандық әдістермен түбірлерін анықтау. Әр түрлі әдіспен анықталған түбірлерді бір бірімен салыстырып қателіктерін көрсету. Дәлдікті өздеріңіз таңдап алыңыздар.
| № | Теңдеулер | түсіндірме |
| (0,2x)3=cos(x) | ||
| x-10sin(x)=0 | ||
| 2-x=sin(x) | X<10 | |
| 2x-2cos(x)=0 | x>-10 | |
| Lg(x+5)=cos(x) | X<5 |
1.1. Берілген сызықты емес теңдеулер жүйелерінің түбірлерін Ньютон, Зейдель, қарапайым итерация әдістерімен анықтау.
| № | Жүйелер | Қосымша шарт |

| ||

| Y=0, y=x, x=0.5 түзулерімен шектелген облыстағы түбірлерін табу. | |

|  Y=0, y=x, x=0.5 түзулерімен шектелген облыстағы түбірлерін табу.
Y=0, y=x, x=0.5 түзулерімен шектелген облыстағы түбірлерін табу.
| |

| Y=0, y=x, x=0.5 түзулерімен шектелген облыстағы түбірлерін табу. | |

| Y=0, y=x, x=0.5 түзулерімен шектелген облыстағы түбірлерін табу. |
2 - СОӨЖ: «Сызықты алгебралық теңдеулер жүйесін шешудің сандық әдістері»
Гаусс, Жордан-Гаусс, квадрат түбірлер, Зейдель, қарапайым итерация әдістерін қолданып төмендегі жүйелерді шешу.
№1 №2

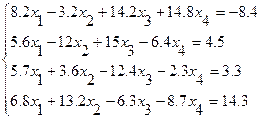
№3 №4


№5

3 – СОӨЖ: «Функцияны интерполяциялау»
Функцияның мәндер таблицасы берілген:
| Х | 1,50 | 1,54 | 1,56 | 1,60 | 1,63 | 1,70 |
| У | 3,873 | 3,924 | 3,950 | 4,000 | 4,037 | 4,123 |
Лагранж формуласын қолданып көрсетілген нүктелердегі функция мәндерін анықтау:
a) 1,52 b) 1,55 c) 1,58 d) 1,61 e) 1,67.
3. Функцияның мәндер таблицасы берілген:
| Х | 2,0 | 2,3 | 2,5 | 3,0 | 3,5 | 3,8 | 4,0 |
| У | 5,848 | 6,127 | 6,300 | 6,694 | 7,047 | 7,243 | 7,368 |
Лагранж формуласын қолданып көрсетілген нүктелердегі функция мәндерін анықтау:
a) 2,22 b) 2,41 c) 2,78 d) 3,34 e) 3,75, f) 3,88.
3. sin(x) функциясының x=0,  /6,
/6,  /4
/4  /3
/3  /2 нүктелеріндегі мәндерін біле отырып x=
/2 нүктелеріндегі мәндерін біле отырып x=  /12 нүктесіндегі мәнін және қателігін анықтау.
/12 нүктесіндегі мәнін және қателігін анықтау.
4. Cos(x) функциясының x=0,  /6,
/6,  /4
/4  /3
/3  /2 нүктелеріндегі мәндерін біле отырып x=
/2 нүктелеріндегі мәндерін біле отырып x=  /5 нүктесіндегі мәнін және қателігін анықтау.
/5 нүктесіндегі мәнін және қателігін анықтау.
5. y=ex функциясының мәндері таблицамен берілген. Сызықты интерполяциялау формуласын қолданып функцияның берілген нүктелердегі мәндерін анықтау.
| X | 0.50 | 0.51 | 0.52 | 0.53 | 0.54 | 0.55 | 0.56 | 0.57 | 0.58 | 0.59 | 0.60 |
| ex | 1.6487 | 1.6653 | 1.6820 | 1.6989 | 1.7160 | 1.7333 | 1.7507 | 1.7683 | 1.7860 | 1.8040 | 1.8221 |
|
|
|
|
|
|
Дата добавления: 2017-01-14; Просмотров: 1062; Нарушение авторских прав?; Мы поможем в написании вашей работы!