Байланыс энергиясы. 2 страница

Кристалдық қатты заттар бөлек жалғыз монокристалдық және поликристалдық кристалдар ретінде кездеседі.

Электронда микроскопиялық және рентгенді- құрылымды зерттеулер көрсеткендей шын монокристалдар нағыз құрылымын аз көрсетеді. Көбінесе олар мозаикалық құрылымда болады. Бұл жағдайда барлық монокристалдар 10^{-6 м өлшемді мозаика блоктарына бөлінеді. Мозаика блоктары бір-бірінен бетімен бөліген 10-152}-тен 10-15¹-ке дейінгі әртүрлі монокристалдар үшін блок жұқалығы нормальды разорменацияның максималды бұрышын құрайды.

Кристалдың поликристалдарына жиі құрылымдық жағынан монокристалдар-ға өте жақын. 10^-6м ретінде өлшемде болатын кристалиттер саны мен қатар мозаика блоктарына бөлінеді. Әрбір мозаика блогының өзінің идеалдық құрылымы болады, бірақ блоктар бір қатарға орналастырылмаған, керісінше, бірнеше минуттан бірнеше градусқа дейінгі уақытта бұрылған ретінде орналасқан.

Кристалдық заттардың ерекше құрылымы болып атомдардың қайтарымды орналасуындағы корреляция нақтылығы табылады. Мұндай корреляция өте көп күштердің тепе – теңдігіне немесе атомдардың өзара қарым – қатынас барысында пайда болатын процестерге шартталған. Мұндай тепе – теңдік жағдайында атомдар берілген кристалдарға симметриялық узор жасай ретті орналасады.

Кристалдар бұл геометриялық заңдылықтарға қатысты құрылымдар қатаң периодты орналасқан бөліктерді құрайтын зат. Әрбір кристалдық зат басқа кристалдық заттан атомдық құрылымымен ерекшеленеді.

Қатаң заңдық реттеуде және кристалдар құрылымының симметриясы біркелкі әрі анизатропты. Құрылымдық кристалды графында біркелкі түсінігі анықталған мәнді береді. Кристалл біркелкі деп аталады, егер соның ішінен алынған кез – келген нүктеден қасиеті жағынан бірінші және одан бірнеше қашықтықта қалған идентивті нүкте табылады. Органикалық емес кристалдар үшін бұл алшақтық бірнеше анометрлерді құрайды. Қандайда бір атомдар нүктелеріне міндетті түрде байланысты емес, шығарым кез келген болуы мүмкін етіп ерекшелейміз.

Біркелкі анықтадан шығып және атомдық дискреттік құрылымды ескере отырып, идентивті нүктелердің бастапқы және соңғы компланарлы емес векторымен берілетін тремя нүктесін көрсетуі мүмкін. Барлық кристалдық аралықты қамтитын үш өлшемді периодты торды ескереді. Кристалл структурасы мен кеңістік тор түсінігін ажырату керек. Кристалл структурасы – бұл физикалық шындық.

Торды периодтық қайталаудың элементарлы параллепипед кеңістігінің көмегімен үлес компланарлы вектордың берілуін және а,в,с бірлік трансляцияларды бейнелеуге болады. Трансляция тордың бір нүктесіне ғана емес, барлық торға толық әсер етеді. Үш векторлы трансляция басында кез келген нүктені таңдауға болады. Егер қандай да бір түйін басынан алынса, R векторлы – радиус басқа кез келген тор түйінінде 1.1 формуладан анықталады.

R=ma+nb+pc (1.1.)

Мұнда m,n,p – берілген түйіндердің индекс сандары. Үш индекс жиынтығы қарапайым түрде көбінесе екі квадраттық жақшада жазылады және түйін символы деп аталады.

Жалпы жағдайда элементар ұяшық a,b,c паралелепипед қоры мен байланысты бұрышты және λ(= 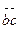), В=(= ), және γ(=ab) бұрыштарын көрсетеді. Алты көрсетілген көлем параметр торы деп аталады. Элементарлы ұяшықтар өлшемін анықтайтын a,b,c параметрлері әрдайымғы тор деп аталады. Элементарлы параллелепипед қысқа a,b,c трансляциясында орналасқан және параллелепипед торының негізі болып табылады. Мұндай параллелепипедтерде ішкі және үстіртін нүктелерде қосымша түйіндер болмайды, тек жоғарғы жағында ғана және оны прементивті немесе примитивті элементарлы ұяшық болып табылады. Негізгі элементарлы параллелепипед көлемінде тордың бір түйіні кездеседі. Параллелепипедтің жоғарғы жағынан алынған әрбір түйін бірдей уақытта параллелепипедке жатады, яғни әрбір параллелепипедке 1/8 түйіннен болады. Параллелепипед ұзындығы 8 болса, онда оған толық түрде 8 х1/8=1 түйіні жатады.

Кейде толық элементарлы ұяшықты таңдаудан гөрі, көп көлемде таңдауға тура келеді. Бұл приментивті параллелепипед сыбайлас бұрышты болып келуі мүмкін. Мысалы кристалл структурасын анықтау барыснда сыбайлас емес координат жүйесінде шығару қатар тік бұрышты да болады. Таңдалынған координаттар ұяшығы жүйесінде жоғарғы жақын түйіндерден басқа қосымша түйіндерден құралуы мүмкін. Күрделі ұяшық координаттар түйінінің сипатталады. Элементарлы ұяшықта туындайтын координаттар түйінінің жиынтығы ұяшық базисі деп аталады. Көбінесе қиын элементарлы ұяшықты қосымша түйіндері центрлік шетте пайда болатындай немесе центр көлемінде пайда болатындай етіп таңдайды. Төменде оданда күрделі кең таралған ұяшықтар орналасуы келтірілген. Центрлік көлемдегі ұяшық.J ұяшығында қосымша түйін В түйінінде жатыр. Мұндай ұяшыққа екі түйін керек: ұяшықтың жоғарғы координатымен А түйінімен ұяшық центрінде табылатын В, бұл ұяшық тығыздығына жатады және [[1/21/21\2]] координаттарды қабылдайды. Сәйкес ұяшықтар периодтары бөлігінде – ½ а, ½ в, ½ с координаттары берілген.

Ұяшық базисі: [[000]]; [[1/2 ½ 1/2]].9zis0 r – ktv3 ұяшық көлемі бойынша центрлік болып табылуын белгілеу үшін мұндай ұяшықтар J ұяшығы деп аталады.

Базо – центрлік ұяшық – центрге негізделген ұяшық. Мұндай ұяшықтарды шек центрленгендігін көрсететін С ұяшығы деп те атайды. Базо – центрлі ұяшықта екі түйін бар: А – жоғарғы [[000]] координаттары және С шегіндегі [[1/2 ½ 0]] координаттарымен В түйіні. В түйінінің қырға жартылай жататындығын көру оңай, ал екінші жартысы көрші ұяшықта жатады. Ұяшықта қыр екеу болса, онда ұяшық қырында табылатын 2х1/2=1 түйіні жатады. Ұяшық базисі: [[000]]; [[1/21/20]]. Бокоцентрлі ұяшық Мұндай ұяшықтар екеу болуы мүмкін: қыр а перпендикуляр осіне орталықтанған А ұяшығы және в перпендикуляр осіне орталықтанған қыр. Тағыда осындай ұяшыққа екі түйін координаттары керек: А – [[000]] түйіні, В – [[1/20 ½ ]] немесе [0 ½ ½ ] түйіндері. Қырлы – центрленген немесе Ғ – ұяшығы (1.7 - сурет). Қосымша түйіндер қыр центрінде табылады. Ұяшыққа төрт түйін қажет. Ұяшық базисі: [[000]];[0,1/21/21/2]; [[1/201/2]]; [[1/21/20]].

2.1 Кристалдар симметриясы. Табиғатта моногрантты түрдегі дұрыс сыртқы формадағы кристалдар жиі кездеседі. Мұндай жағдайда кристалдарды симметриялы болып келеді деп атайды. Кең мағынада симметрия сөзі объекті нақтылығына және қандайда бір өзгермейтін құбылыстың пайда болуына бөлінеді. Геометриялық фигуралар симметриясы құралдары тең және біркелкі орналасқан бөлікті құрайды. Қандайда бір осьтің айналу шеңберінде өздігінен нүктенің бейнеленуінде немесе фигура тығыздығында араласу мүмкін. Мұндай операциялар симметриялы мамандандырылған, симметрияны бөлек сипаттайтын бейне – симметрия элементі деп аталады. Барлық денені барлық геометриялық фигуралар сияқты жүйе нүктесі ретінде қарастыруға болады. Әрбір соңғы фигураның ең болмағанда бір нүктесі бар. Мұндай нүкте ерекше болып табылады. Бұл жағдайда кристалдар симметрия кеңістігін алмағанда, трансляция болып табылатын негізгі симметрия элементі кристалдық тор үшін сипатталатын нүктелік симметрияны ерекшелейді.

Кристалда симметрия элементтерінің саны шеклеулі. Бұларда соңғы фигуралардағыдай келесі негізгі симметрия элементтеріне бөлінеді: айналық симметрия тығыздығы, симметрияның бұрылым осі, симметрия центрі немесе инверсия центрі.

Симметрияның айналық тығыздығы айна секілді қарапайым тығыздық бейнесіне сәйкес келеді. Мұндай тығыздық денені теңдей екі бөлікке бөледі. Осы тығыздықты бейнелеуде басқа барлық нүктелермен өзара сәйкес келетіндей. Симметрияның қарапайым бұрылу осьі – айналу бөліміндегі бұрылуындағы түзу сызық, яғни 1/n тең. Мұндай n – ось реттігі, фигура өздігінен барлық нүктелерінде араласады, қосылады. n=6 алтылық ретті фигура осінде мұндай бұрылу 1/6 айналымға тең. Қарапайым бұрылу осінен басқа айналық бұрылу осі 1/n айналымдағы остің бұрылу әрекетіндегі бірдейлікті ескеретін және тығыздық перпендикулярлық бейнесіне бөледі. Симметрия центрі немесе инверсия центрі – фигура ішіндегі басты нүктесі. Кристалдарда симметрия осьтері бес әртүрлі атауларда кездеседі: бірінші, екінші, үшінші, төртінші және алтыншы. Кез келген көп қырлы кристалдарда симметрия элементтерінің шектеулі сандары болады. Симметрия элементтерінің толық жиынтығын жалпы жағдайда симметрия класы деп атайды. Симметрия кластары саны бойынша немесе симметрия элементтерінің орналасуы бойынша ерекшеленеді. Кристалдарда кездесетін симметриялық элементтер комбинациясының барлық мүмкін математикалық анализі осындай комбинациялар санының шектеулі екендігін және кристалдық кластар санының шектеулілігін көрсетеді. Кристалл бейнесін сыртынан зерттеу 32 класс симметриясын орнатуға алып келеді. Бұл симметрия ішкі структурасына тікелей тәуелді және дискретті жиіліктердің шектік торда орналасуын анықтайды. Жоғарыда қарастырылған шектік тор элементтері – симметрия тығыздығы, симметрия осі, симметрия ортасына тордың бір ғана нүктесіне емес, барлық торға әсер ететін жаңа симметрия элементі Т трансляция қосылады. Торды трансляцияға араластыру барысында вектордың бағытталуы тор трансляциясы барлық нүктелерінде бірігеді. Трансляция комбинациясы симметрия элементімен соңғы фигура кристалы ретінде симметрия элемнтінің жаңа түрін береді. Мұндай элементтер болып: ось бойымен бұрылу +параллельді осьтің берілуі= винттік ось; тығыздық бейнесі + тығыздықтың параллельді бөлінуі=тығыздықтың сырғанау бөлігі болып табылады. Табиғатта мысалға, қантты және басқада оң және сол кристалды кварцтар кездеседі. (1.8 – сурет). Барлық мүмкін симметриялық тордағы жағдайларды зерттеу келесі элементтерден – айналық тығыздық, қарапайым бұрылу ось, симметрия центрі сығу бөлігінің тығыздығы, әртүрлі атаулардағы винттік осьтер топтық шектегі шектеулі сандармен көрсетуге болады. Анықталған бейнеде 32 кластық нүктелік симметрияға жататын симметрияның 230 шектік тобы Е.С.Федорова толық қорытындыға келтірді.

2.2. Кристалдардың координатының жүйесі. Кристалды – графикада кристалдардың аналитикалық бейнеленуі үшін сәйкес кристалл симметриясымен таңдалатын үш өлшемді координат жүйесін қолданады. Координат осьтері алты параметрмен сипатталатын a,b,c,α,β,γ элементар ұяшықтармен сәйкес келеді. Кристалды – графикалық осьте таңдау кезінде ережелерді сақтау қажет, яғни кристалды – графикалықта қабылданған және міндетті барлық зерттеулер үшін. Бұл заңдылықтардың орындалуы мүмкін жағдайын шығарады. Координат осьтерінің орналасуы кристалл графикалық индекстерге тәуелді екендігін есте сақтау қажет. Барлық кристалл графикалық оқулықтарда жетінші сингоникалық деп фомбоэдрикалық примитивті ұяшыққа сәйкес тригональдарын санайды.. Мұндағы гексогельді сингонтригональды байланыс біз көріп отырғандай торда болады. Әрбір кристалдық структураны элементарлы трансляция жиынымен сипаттауға болады.

О. Бравэ 1848 жылы трансляциялық тордың 14 типі бар екендігін математикалық жолмен дәлелдей алды. Бравэ мынандай үш шартты қарастырды:

1. Таңдалынған ұяшық барлық тордың сингониясы болуы, оның симметриясы барлық тор симметриясына сәйкес болуы тиіс;

2. Тік бұрыш саны және теңдік жағы максимальды болуы тиіс.

3. Алғашқы екі шартты сақтау барыснда ұяшық көлемі минимальды болуы тиіс.

Олай болса, элементарлы ұяшықты стандартты таңдауға сәйкес кристалдың сыртқы симметриясы мен сақталынған жоғарғы үш шарттың кез келген кристалдық структурасы Бравэнің әртүрлі торының 14 топологиясының біреуінің көмегімен көрсетілген. Осы 14 тордың ішінен тек 6 ғана примитивті болады. Вингер – Зейц ұяшығының негізгі примитивті ұяшық көлемі бойынша тең.

2.3. Түзу және түйіндік тығыздықтағы кристалл графикасының символдары.

Кристалл графикада тығыздық алынған және шектік торды түйін арқылы жүргізеді. Алда бізді тек «түйінді тығыздық» пен «түйіндік түзу» қызықтырады.

Түйінді тығыздықтар. Олардың үш түйін арқылы өтетін бір түзуде жатпайтын барлық тығыздық толық сетка түйінін құрайды. Параллель түйіндер тығыздық жүйесі бір – бірінен бірдей d қашықтықтағы тығыздық аралығында орналасқан.

Жалпы декарттық координата жүйесі ретінде примитивті ұяшық қырын аламыз. Шектік торда түйін арқылы өтетін қандай да бір тығыздықты жүргіземіз. Ол координат осінде нүктемен белгіленген. Таңдалған жүйе координатында мұндай тығыздық бірінші дәрежелі теңдеумен шығарылады:

Ax+By+Cz+D=0 (1.2)

О координат басында сыртқы параллельді трансляционды және идентивті болып табылатын тығыздық өтеді. Бұл тығыздық теңдеуі мына түрде болады:

Ax+By+Cz=0 (1.3)

Осы тығыздықтан екі түйін координатасымен алайық

X₁=m₁a; y₁=n₁b; z₁=p₁c; X₂=m₂a; y₂=n₂b; z₂=p₂c мұнда m₁,n₁,p₁,m₂,n₂,p₂ – бүтін сандар, a,b,c – элементарлы ұяшық параметрлері.

Координаттар түйіні (1.3) теңдеуі қанағаттандыратындығы белгілі:

Ааm₁+Bbn₁+Ccp₁=0; Aam₂+Bbn₂+Ccp₂=0

Сызықтық теңдеу теориясынан Аа, Вb,Cc t көбейтіндіге дейін дәл анықталуы тиіс:

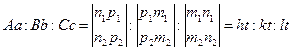(1.4)

m,n,p – сандар, h,k,l - өзара үш қарапайым сандар. Егер (1.3) теңдеуіндегі А,В,С коэффициенттерінің орнына мәндерді қоятын болсақ, онда басынан өтетін тығыздық теңдеуі мына түрде болады.

hx+kx+lx=0 (1.5)

Мұнда x=x/a; y=y/b; z=z/c - әрбір осьтегі әртүрлі бірліктер және элементар ұяшық қырының трансляциясына тең. Кез келген тығыздық теңдеуі, басынан өтетін параллельді тығыздық былай жазылады:

Hx+ky+lz=t (1.6)

Мұнда t – бүтін сан. Басы арқылы өтетін тығыздық үшін t=0, ал басына жақын болса t=1.

Егер (1.6) теңдеуі t=1 жағдайында кескінді тығыздығындағы теңдеу түрінде жазылады:

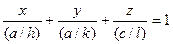(1.7)

1.14 – те екі өлшемді ұяшықтың параллельді тығыздық типі келтірілген.

Күрделі торды бірнеше біркелкі параллельді примитивті торлардан құралған ретінде қарастыруға болады. Осы примитивті тор саны үйіндер санына тең, ал оның бастапқы түйіндері примитивті емес тор түйіндерінен табылады.

Егер ұяшық көлемі бойынша орталықтанған болса, онда диоганаль жұп санда h+k+l=2n болады. Мұнда n – бүтін сан. Егер h+k+l=2n+1 суммасы тақ болса, онда диоганаль өзгереді. Кубтық кристалда (110),(101),(011) тығыздықтары эквивалентті. Мұндай эквивалентті тығыздықтар {110} символымен анықталады немесе жалпы жағдайда {hkl}.

Тығыздық жағдайын анықтауға гексагональдық кристалда үш жүйе емес, координаттың төрт осі пайдаланылады. Әр тығыздық төртінші индекс І жасайды. Төртінші а₃ көмекші осі с перпендикуляр ось тығыздығына кіреді. АВ түзуі – тығыздық ізі, ОД – р кесіндісі, ал ΔΑΒC мен ΔΑДО – дан мына формула шығады:

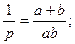
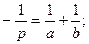
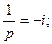
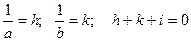- (1.8)

Төрт индексті әдіс гексагональды кристалда мәндерді анықтаумен ыңғайлы. Мысалы бізге теңдей мәндерді (213) тығыздық типі шығару қажет. Тығыздық төрт индекс жүйесінде (213), і=n – (2+1)=3 жазсақ, онда (2.13) – (2133) болады. Циклдық орналастыруды пайдалана отырып (1.17) – суреттен қалған тығыздықты жазу оңай:

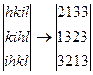
Үшінші қатарды белгілеу арқылы үш индексті жүйедегі теңдей мәнді тығыздыққа өтеміз.

Гексагональды тығыздық кристалында с перпендикуляр осі - тығыздық базисі гексагональды призманың негізі болып табылады және (0001) индексті болады. Параллель призма қырының тығыздықтары мына индекстерді қабылдайды (1010),(0110),(1100),(1010),(0110),(1100).

Түзу түйіндер. Шекаралық торда xyz координатты кристалл графикалық жүйені көреміз және координат басынан түзу түйіндерді жүргіземіз. [[mnp]]

Түйін символы түзу символға және [[mnp]] квадрат жақшаға жазылады. Мұнда m,n,p бүтін параллельді түзу түйіндерін сипаттайды. Белгілеу үшін симметриялы эквивалентті түзу түйіндерін жиынтығымен жұмыс жасаймыз, яғни <mnp> символы түрінде. Мысалы координаттық осьтердің кубтық кристалдарға [100],[010],[100],[001],[010],[001] бағытталу күш симметриясында эквивалентті. Сондықтанда мұндай жиынтық <100> символын береді.

3-лекция. Кристалдың кеңістіктік торы.

Қатты дене физикасында көп жағдайларда талдауда периодтық потенциал өрісіндегі электрондар қозғалысы дискреттік жиіліктің периодтық орналасу байланысында қайтару торы басты және пайдалы рөлді атқарады. Қайтару торы кристалда болмайды, ол математикалық шарттарды дәл бейнелейтін ыңғайлы абстракцияны көрсетеді, а,в,с векторлық трансляцияда орналасқан қарапайым түзу торының параметрі мен қайтару торы параметрлері аралығында анықталған байланыс бар. Осы байланысты орнату үшін x,y,z координаттарына жақын (hkl) тығыздығын жүргіземіз. (hkl) тығыздығы (100), (010) және (001) координаттар тығыздығымен бірге отырып АОВС тетраэдрін құрайды. Егер тетраэдрдың үшбұрыш қырының S ауданы векторға сәйкес болса, онда жабық жоғарғы векторы әрдайым нөлге тең санау векторлық теоремасымен келіседі және мына түрде жазамыз:

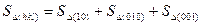(1.9)

Тетраэдр ауданын тетраэдрдың V көлемді формуласынан шығаруға болады V=1/3SH бұдан

S=3V/H (1.10)

Мұндағы Н – тетраэдр биіктігі. (1.9) мен (1.10) формулалардан (1.11) формула шығады:

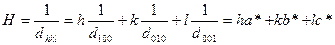(1.11)

Мұндағы а*,в*,с* - кері торының осьтік векторы. (1.9) мәнінің оң жақ бөлігіне сәйкес векторды қоя отырып мынаны аламыз:

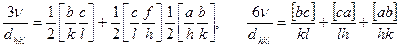
6ν=a[bc/hkl)=V_βx/hkl), мұнда ν_яч – а,в,с векторында орналасқан элементар ұяшық көлемі болса, онда

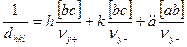(1.12)

(1.11) мен (1.12) формуласын салыстыра отырып (1.13) формуласын аламыз:

а* 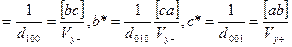(1.13)

(a[bc])=(b[ca])=(c[ab])=V_яч болса, онда скаляр есептеу

(aa*)=(bb*)=(cc*)=1, (bc*)=(b*c)=(ca*)=(ab*)=(a*b)=0 (1.14)

Соңғы (1.14) алты теңдеу мәні кері торының тұрғызылу ережесін көрсетеді. Олар: 1)а*,в*,с* векторларын тұрғызудағы перпендикуляр векторлар в және с, с және а, а және в парларына сәйкес.

2) а,в,с векторлары в* және с*, с* және а, а* және в* векторларына сәйкес перпендикуляр.

Түзу тор векторы кері торы векторының аналогиялық формуласымен байланысты:

a=[b*c*]/v*, b=[c*a*]/v, c=[a*b*]/v (1.15)

Мұнда V* - кері торының элементар ұяшық көлемі.

(1.13) – ті а – ға скаляр көбейтеміз. (1.13) пен (1.15) – тен (1.14) – ке қатысты мынадай қатынасты аламыз.

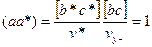бұл жерде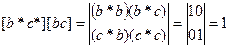

Сонда V*=1/V_яч болады. Алынған нәтижеден түзу және кері торы өзара орайластық екенін көреміз. Әрбір кері [[hkl]] торының түйіні параллельді түзу торының (hkl) тығыздығымен сәйкес келеді. Қайтару торының Н=ha*+kb*+lc* векторы (hkl) тығыздығына перпендикуляр және модулі бойынша 1/d_hkl – ға тең. Мұнда d_hkl - түзу торының {hkl} эквиваленттік тығыздық жүйесіндегі тығыздық аралық қашықтық. Бұл ұзындықтағы көлемді есептеуде (1.11) алынған формула пайдалы.

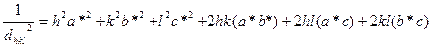(1.16)

Ыңғайлы және қарапайым скалярлық есептеуде келесіні пайдалану қажет

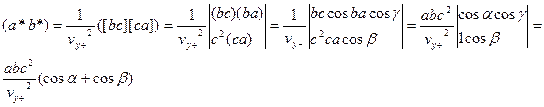
Мұнда 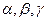- сәйкес трансляция бұрыштар. Тікбұрышты ұяшық үшін a*=1/a;

b*=1/b; c*=1/c және (a*b*)=(a*c*)=(b*c*)=0, сонда 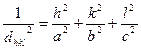(1.17)

Кубтық ұяшық үшін a=b=c, сондықтанда қайталау мәніндегі тығыздық аралық қашықтық квадраты:

(1.18)

(1.16) қолдана отырып 1/d_hkl² мәнін алуға болады. Жалпы жағдайда элементар ұяшық көлемін есептеу аналитикалық геометриялық формуласымен шығарылады:

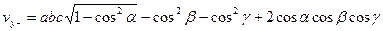
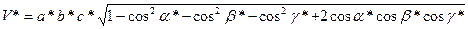(1.19)

Мұнда а*=(b*c*), β*=(c*a*), γ*=(a*b*) – қайтару торындағы вектораралық бұрыштар.

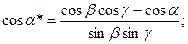
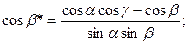
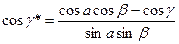(1.20)

Тығыз оралған шарлар. Кристалдық құрылым мысалы.

Көптеген кристалдық қатты денелер нейтральды атомдардан немесе теріс және оң ионды зарядтардан құралған. Көпшілік химиялық элементтердің атомдары мен иондары сфералық симметрияны құрайық.

Егер атомдар мен иондарды өзара тебілу және тартылу күші әрекетіндегі жиырылмайтын қатты шарлардан көрсек, онда құрылым негіздерінің кристалдық структурасының көпшілігін шартты түрде түсінуге болады. Шарларды оралым үлкен симметриялы және компактты түрде болатындай етіп орналастырайық. Әсіресе кеңістікте тығыз оралған оралымдардың тұрғызылуы жіңішке тығыз қабатталған шарлардан тұрады. Тығыз оралған шарлардың бірдей радиустары 1.21 жазықтығында көрсетілген. Жазықтық қабатында әрбір шар мысалы, А басқа алты шармен және сәйкес алты бос үшбұрыш кемтігімен қоршалған, ол әрбір үш шарға 1/3 – тен тиеді. Бұдан яғни, әрбір шарға 6х 1/3=2 кемтіктен келеді.

Дата добавления: 2017-02-01