Тест по економетрії

Вибрати правильну відповідь на запитання:

1. Лінійна регресія:

а) лінія, що відображає зв’язок між незалежною і залежною змінними;

б) інша назва простої регресії;

в) лінія, яка завжди має нахил, що дорівнює 1;

г) графік значень незалежної і залежної змінних;

д) лінія, яка завжди має нахил, що дорівнює 0

.

2. Нахил:

а) точка, де лінія регресії перетинає вісь у;

б) вимірює придатність лінії регресії;

в) вимірює зв’язок між залежною і незалежною змінними;

г) завжди дорівнює 1;

д) інша назва коефіцієнта детермінації

.

3. Перетин:

а) точка, де лінія регресії перетинає вісь у;

б) вимірює придатність лінії регресії;

в) вимірює зв’язок між залежною і незалежною змінними;

г) завжди дорівнює 1;

д) завжди дорівнює 0

.

4. Що з наведеного не є припущенням моделі лінійної регресії:

а) або  є сталими числами, або вони є статистично-незалежними від випадкових величин ;

б) дисперсія випадкової величини  є сталою;

в) математичне сподівання випадкової величини  дорівнює нулеві;

г) дисперсія випадкової величини дорівнює 0;

д) випадкові величини є статистично незалежними одна від одної

.

5. Коефіцієнт детермінації:

а) точка, де лінія регресії перетинає вісь у;

б) вимірює придатність лінії регресії;

в) вимірює зв’язок між незалежною і залежною змінними;

г) завжди дорівнює 1;

д) завжди дорівнює 0

.

6. Коефіцієнт детермінації вимірює:

а) варіацію незалежної змінної;

б) нахил лінії регресії;

в) перетин лінії регресії;

г) загальну варіацію залежної змінної, що пояснюється регресією;

д) завжди дорівнює 1

.

7. Сума квадратів, що пояснює регресію:

а) ;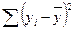

б) ;

в) ;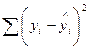

г) ;

д) .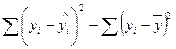

8. Сума квадратів помилок:

а) ;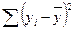

б) ;

в) ;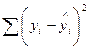

г) ;

д)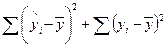

9. Коваріація між х та у є:

а) ;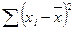

б) ;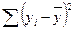

в) ;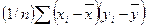

г) r _yx

д) в і г.

10. Якщо ми хочемо, використовуючи регресійний аналіз, виміряти зв’язок між досвідом роботи і заробітною платою, то:

а) незалежною змінною має бути заробітна плата;

б) незалежною змінною має бути досвід роботи;

в) залежною змінною має бути заробітна плата;

г) залежною змінною має бути досвід роботи;

д) б і в

.

11. У регресії: у=0,34+1,2х нахил дорівнює:

а) х;

б) у;

в) 0,34;

г) 1,2;

д) 1,2/0,34.

12. У регресії: у=0,34+1,2х перетин дорівнює:

а) х;

б) у;

в) 0,34;

г) 1,2;

д) 1,2/0,34.

13. З урахуванням співвідношення між заробітною платою (в гривнях) —у і освітою (в роках) —х, у=12,201+525х, особа, яка навчалася додатково один рік, може очікувати на таку додаткову оплату:

а) 12,201;

б) 525;

в) 24,402;

г) 1,050

д) 12,201+525.

14. З урахуванням співвідношення між заробітною платою (в гривнях) — у і освітою (в роках) — х, у=12,201+525х, особа, що навчалася додатково нуль років, може очікувати на таку додаткову оплату:

а) 12,201;

б) 525;

в) 24,402;

г) 1,050;

д) 12,201+525.

15. Якщо регресія має R²=0,80, то регресійна лінія:

а) пояснює 80% варіації змінної х;

б) пояснює 80% варіації змінної у;

в) матиме нахил 0,80;

г) матиме перетин 0,80;

д) не пояснює зв’язку між х і у.

2.5. Інші критерії якості лінійної регресії

Припустимо, відомі n прогнозних даних , що відповідають n

реальним даним у₁, у₂, у₃, …, у_n, тобто маємо відповідно n помилок прогнозу е₁, е₂, е₃, …, е_n . Для визначення якості прогнозу (моделі) на практиці широко використовуються такі критерії:

:

1. Середня помилка прогнозу:

                                                       (2.5.1)

Цей критерій характеризує ступінь зміщення прогнозу і для правильних прогнозів повинен прямувати до 0 за умови великої кількості спостережень, тобто

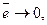при .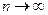

2. Дисперсія помилок:

                                                   (2.5.2)

та стандартне відхилення:

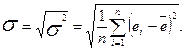                                 (2.5.3)

Цей критерій вимірює ступінь розкиду значень змінної навколо свого середнього значення.

Для простої лінійної регресії середнє значення помилок дорівнює нулеві. Тому

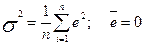.                                          (2.5.4)

3. Абсолютне середнє відхилення:

.                                                  (2.5.5)

4. Середній квадрат помилки:

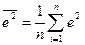. (2.5.6)

Цей критерій для лінійної регресії збігається з дисперсією помилок

.

5. Абсолютна середня процентна помилка:

.                                           (2.5.7)

Цей критерій використовується при порівнянні точності прогнозів різнорідних об’єктів, бо характеризує відносну точність прогнозу. При цьому вважається, якщо значення цього критерію менше 10% — висока точність прогнозу, а отже, і якість моделі; від 10 до 20% — добра точність; від 20 до 50% — задовільна точність; понад 50% — незадовільна точність

.

6. Середня процентна помилка:

.                                             (2.5.8)

Це показник незміщеності прогнозу. З точки зору практики для якісних моделей цей показник має бути малим, загалом не перевищувати 5%. Зазначимо, що як і показник 5, він не визначений для нульових значень у [5]

.

7. Середня абсолютна помилка:

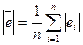
Примітка: Для розрахунку вищеперелічених критеріїв варто використати таблицю:

№
. . . n

Завдання 17. Перевірити якість лінійної регресійної моделі, побудованої в завданні 4, за допомогою критеріїв:

Зробити висновки.

Завдання 18. Перевірити якість лінійної регресійної моделі, побудованої в завданні 8, за допомогою критеріїв:

Зробити висновки.

Завдання 19. Перевірити якість лінійної регресійної моделі, побудованої в завданні 10, за допомогою критеріїв з розділу 2.5. Зробити висновки.

Завдання 20. Перевірити якість лінійної регресійної моделі, побудованої в завданні 11, за допомогою критеріїв з розділу 2.5. Зробити висновки.

2.6. Математичне сподівання та дисперсія розподілу параметрів  b₀ та b₁ . Оцінка дисперсії випадкової величини .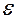

1. Математичне сподівання параметра b₀дорівнює:

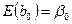.                                                (2.6.1)

             2. Дисперсія параметра b_0:

    (2.6.2)

         3. Математичне сподівання параметра b₁ дорівнює:

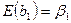.                                                (2.6.3)

   4. Дисперсія параметра b₁:

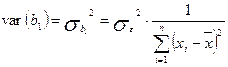,         (2.6.4)

де 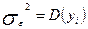 — дисперсія залежної змінної.

                5. Оцінка дисперсії випадкової величини :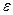

,                                  (2.6.5)

де к — кількість параметрів, що оцінюється в регресійній моделі. Для простої лінійної регресії:

.                         (2.6.6)

Середнє квадратичне відхилення оцінки дисперсії:

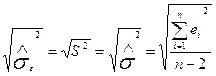.            (2.6.7)

Оскільки випадкова величина 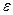 — неспостережувана, то і її дисперсію неможливо обчислити, тому на практиці дисперсія випадкової величини  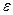замінюється на свою оцінку.

У виразах (2.6.2) та (2.6.4) дисперсія параметрів b₀ та b₁ — невідома, оскільки вона залежить від дисперсії помилок  випадкової величини 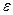, котру неможливо спостерігати. Отже, для параметрів b₀ та b₁ дійсна дисперсія замінюється своєю оцінкою [5]:

;                       (2.6.8)

                         (2.6.9)

Приклад 5.Визначити оцінку дисперсії та середнього квадратичного відхилення для параметрів b₀ та b₁ лінійної регресійної моделі, побудованої в прикладі 1.

Рішення:

  Для параметра b_1:

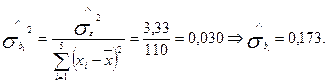
  Для параметра b_0:

Завдання 21. Визначити оцінку дисперсії та середнього квадратичного відхилення для параметрів b₀ та b₁ лінійної регресійної моделі, побудованої в завданні 4.

Завдання 22. Визначити оцінку дисперсії та середнього квадратичного відхилення для параметрів b₀ та b₁ лінійної регресійної моделі, побудованої в завданні 8.

Завдання 23. Визначити оцінку дисперсії та середнього квадратичного відхилення для параметрів b₀ та b₁ лінійної регресійної моделі, побудованої в завданні 10.

Завдання 24. Визначити оцінку дисперсії та середнього квадратичного відхилення для параметрів b₀ та b₁ лінійної регресійної моделі, побудованої в завданні 11.

Завдання25. Маємо таку інформацію:

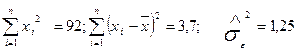; n = 40

а) визначити 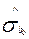;                  б) визначити .

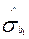2.7. Перевірка значимості параметрів b₀  та b₁ вибіркової лінійної регресійної моделі за допомогою t-теста Стьюдента

t-тест Стьюдента для перевірки значимості параметрів b₀ та b_1, визначених методом найменших квадратів, має вигляд:

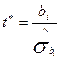.                           (2.7.1)

За таблицею t-розподілу Стьюдента визначають  — критичне значення
з (n-2) ступенями вільності та 5%-рівнем значимості.

Якщо 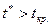, то параметр b_i — статистично значимий [5].

Приклад 6.  Перевірити значимість параметрів b₀ та b₁ лінійної регресійної

                 моделі, побудованої в прикладі 1, за допомогою

                 t-теста Стьюдента.      

 .  

Рішення:

     Для параметра b₁ та b₀:

_;

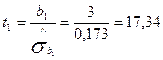Примітк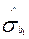а:  та 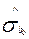 розраховані в прикладі 5. За таблицею t-розподілу Стьюдента визначимо — критичне значення з n-2=5-2=3 — ступенями вільності та 5%-рівнем значимості:

.

Оскільки, t₁=17,34 > t_кр.=3,182;

t₂ = 5,21 > t_кр.=3,182.

Отже, параметри b₁ та b₀ статистично значимі.

Завдання 26. Перевірити значимість параметрів b₀ та b₁ лінійної регресійної моделі, побудованої в завданні 4, використавши t-тест Стьюдента.

Завдання 27. Перевірити значимість параметрів b₀ та b₁ лінійної регресійної моделі, побудованої в завданні 8, використавши t-тест Стьюдента.

Завдання 28. Перевірити значимість параметрів b₀ та b₁ лінійної регресійної моделі, побудованої в завданні 10, використавши t-тест Стьюдента.

Завдання 29. Перевірити значимість параметрів b₀ та b₁ лінійної регресійної моделі, побудованої в завданні 11, використавши t-тест Стьюдента.

2.8. t-тест Стьюдента для оцінки значимості коефіцієнта кореляції

t-тест для оцінки значимості коефіцієнта кореляції (з припущенням, що ):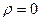

,        (2.8.1)

де r — вибірковий коефіцієнт кореляції між х і у;

n — кількість спостережень.

Величина t* розподілена за t-розподілом Стьюдента з (n-k)- ступенями вільності (для простої лінійної регресії к=2).

Розраховане значення t* порівнюємо з критичним 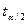 при -ному рівні значимості й (n-2)-ступенях вільності. Якщо 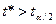, відкидаємо нуль-гіпотезу і приймаємо гіпотезу , тобто робимо висновок, що коефіцієнт кореляції — статистично значимий [5].

Приклад 7. Маємо вибірку значень х і у, яка складається з 5 спостережень,коефіцієнт кореляції r _yx = 0,995. Перевірити при 5%-ному рівні значимості, чи значимо коефіцієнт кореляції відрізняється від нуля.

Рішення: t-статистика Стьюдента:

.

За таблицями Стьюдента знаходимо критичне значення (t_кр.) з 3-ма ступенями вільності і 5%-ним рівнем значимості, яке дорівнює 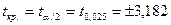.Оскільки,t* =17,23 > t_кр. = 3,182, то робимо висновок, що , тобто коефіцієнт кореляції значимо відрізняється від нуля.

Завдання 30. Перевірити при 5%-ному рівні значимості , чи значимо відрізняється від нуля коефіцієнт кореляції, розрахований в завданні 6.

Завдання 31. Перевірити при 5%-ному рівні значимості , чи значимо відрізняється від нуля коефіцієнт кореляції, розрахований в завданні 7.

Завдання 32. Здійснити перевірку значимості коефіцієнта кореляції (при 5%-ному рівні значимості), розрахованого в завданні 8.

Завдання 33. Здійснити перевірку значимості коефіцієнта кореляції (при 5%-ному рівні значимості), розрахованого в завданні 10.

Завдання 34. Перевірити при 5%-ному рівні значимості, чи значимо відрізняється від нуля коефіцієнт кореляції, визначений в завданні 11

.

2.9. Побудова інтервалів довіри для параметрів b₀ та b₁

Для того, щоб визначити, як же параметри b₀ та b₁ вибіркової лінійної регресії пов’язані параметрами b₀ та b₁ узагальненої лінійної регресії, потрібно побудувати інтервали довіри для параметрів [5]:

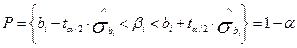 з (n-2) ступенями вільності

або

.                        (2.9.1)

Для 95%-ного рівня довіри:                        

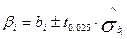.                      (2.9.2)

Приклад 8. Побудувати інтервали довіри для параметрів b₀ та b₁ лінійної регресійної моделі, розрахованої в прикладі 1 (рівень довіри — 95%).

Рішення: Інтервали довіри для параметра b₀ :

 

або

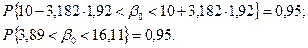
Інтервали довіри для параметра b_1:

   або

Висновок: інтервали довіри для параметра b₁ сталіші, ніж для параметра b_0.

Завдання 35. Побудувати інтервали довіри для параметрів b₀ та b₁ лінійної регресійної моделі, розрахованої в завданні 4 (рівень довіри — 95%).

Завдання 36. Побудувати інтервали довіри для параметрів b₀ та b₁ лінійної регресійної моделі, розрахованої в завданні 8 (рівень довіри — 95%).

Завдання 37. Побудувати інтервали довіри для параметрів b₀ та b₁ лінійної регресійної моделі, розрахованої в завданні 10 (рівень довіри — 95%).

Завдання 38. Побудувати інтервали довіри для параметрів b₀ та b₁ лінійної регресійної моделі, розрахованої в завданні 11 (рівень довіри — 95%).

Завдання 39. Оцінюємо таку регресію:

У=2300 + 10,12х;

n=28.

Перевірити значимість нахилу при 95%-ному рівні довіри. Побудувати 90%-ний інтервал довіри для нахилу.

2.10. Прогнозування за моделями простої лінійної регресії

Приклад 9. За лінійною регресійною моделлю, побудованою в прикладі 1, спрогнозувати обсяг реалізації цукерок при витратах на рекламу в
15 млн. грн.

Рішення: Модель, побудована в прикладі 1, має вигляд: 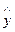= 10 + 3х. Прогнозне значення обсягу реалізації цукерок ( , в млн.коробок) при витратах на рекламу =15 млн.грн. таке:

= 10 + 3 •15 = 55 млн. коробок.

Побудуємо інтервал довіри для залежної змінної 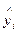, для цього використаємо формулу:

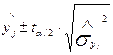 або  , (2.10.1),

де  — оцінка дисперсії залежної змінної, яка дорівнює оцінці дисперсії помилки:

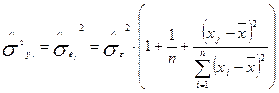(2.10.11),

тобто,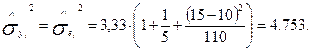

Задамо рівень значимості . За таблицею t-розподілу Стьюдента визначимо 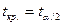— критичні значення з n-2 = 5-2 = 3 — ступенях вільності, котре дорівнює 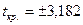. Відповідно інтервал довіри для залежної змінної:

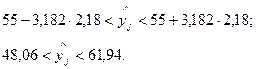
Висновок: при витратах на рекламу в 15 млн. грн. Слід очікувати обсяг реалізації цукерок в межах від 48 до 62 млн. коробок.

Завдання 40. За лінійною регресійною моделлю, побудованою в завданні 4, спрогнозувати урожайність зернових при довільно вибраному (в межах розумного) значенні кількості внесенних мінеральних добрив.

Завдання 41. За лінійною регресійною моделлю, побудованою в завданні 8, спрогнозувати витрати на відпустку при довільно вибраній кількості членів родини.

Завдання 42.За лінійною регресійною моделлю, побудованою в завданні 10, спрогнозувати рівень звільнень на 100 робітників при довільно вибраному (в межах розумного) рівні безробіття.

Завдання 43. За лінійною регресійною моделлю, побудованою в завданні 11, спрогнозувати значення залежної змінної У при довільно вибраному значенні Х.

Завдання 44. Вивчаючи зміну попиту на йогурт залежно від

його ціни, отримано такі результати:

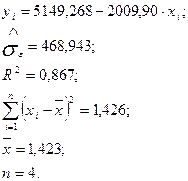
Фірма встановлює на йогурт ціну: 1,75 грн. Спрогнозуйте попит і побудуйте 90%-ний інтервал довіри для математичного сподівання прогнозу.

Примітка: інтервал довіри для математичного сподівання:

Дата добавления: 2023-10-13