Метод Гаусса

Наиболее распространенным среди прямых методов решения систем линейных уравнений является метод исключения Гаусса и его модификации. Он основан на приведении матрицы системы к треугольному виду. Это достигается последовательным исключением неизвестных из уравнений системы. Сначала с помощью первого уравнения исключается x₁ из второго и всех последующих уравнений системы. Затем с помощью второго уравнения исключается x₂ из третьего и всех последующих уравнений. Этот процесс называется прямым ходом метода Гаусса. Он продолжается до тех пор, пока в левой части последнего n -го уравнения не останется лишь один член с неизвестным x_n. Таким образом, матрица системы будет приведена к треугольному виду. К такому виду приводится лишь невырожденная матрица (определитель D ≠ 0).

Обратный ход метода Гаусса состоит в последовательном вычислении искомых неизвестных: решая последнее уравнение, находим единственное неизвестное x_n. Далее, используя это значение из предыдущего уравнения, вычисляем x_n-1 и т.д. Последним находим x₁ из первого уравнения.

Рассмотрим применение метода Гаусса для системы из трех уравнений:

(4.5)

Для исключения x₁ из второго уравнения прибавим к нему первое, умноженное на 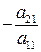. Затем умножим первое уравнение на 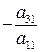и прибавим результат к третьему. Из третьего так же исключится x₁. Получим равносильную систему вида:

(4.6)

где , (i, j = 2, 3), , (i = 2, 3).

Например: , .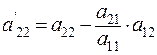

Теперь из третьего уравнения системы (4.6) надо исключить x₂. Для этого второе уравнение умножим на и прибавим результат к третьему. Получим:

(4.7)

где , .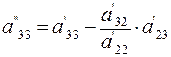

Матрица системы (4.7) имеет треугольный вид. На этом заканчивается прямой ход метода Гаусса.

Заметим, что в процессе исключения неизвестных приходится выполнять операции деления на коэффициенты a₁₁, a₂₂ и т.д. Поэтому они должны быть отличными от нуля. В противном случае необходимо соответствующим образом переставить уравнения системы. Перестановка уравнений должна быть предусмотрена в вычислительном алгоритме при его реализации на ПК.

Обратный ход начинается с решения третьего уравнения системы (4.7):

.

Используя это значение можно найти x₂ из второго уравнения, а затем x₁ из первого:

,

.

Аналогично строится вычислительный алгоритм для линейной системы с произвольным числом уравнений.

Дата добавления: 2014-01-04