Оценивание однородности и направленности изменений финансовых процессов, представленными временными рядами

Успешность статистического анализа развития процессов во времени во многом зависит от правильного построения рядов ди­намики. Так, большое значение имеет выбор интервалов между соседними уровнями ряда. Удобнее всего иметь дело с равноот­стоящими друг от друга уровнями ряда. При этом нежелательно брать слишком большой интервал времени, так как можно упус­тить существенные закономерности в динамике показателя. На­пример, по квартальным данным невозможно судить о месячных сезонных колебаниях, К тому же слишком малые интервалы между наблюдениями увеличивают объем вычислений, а также могу приводить к появлению ненужных деталей в динамике процесса засоряющих общую тенденцию. Разумеется, вопрос о выборе интервала времени между уровнями ряда должен решаться исходя и целей каждого конкретного исследования.

Уровни временных рядов могут содержать аномальные значения или «выбросы». Часто появление таких значений может быть вызвано ошибками при сборе, записи и передаче информации. Возможными источниками появления ошибочных значений могут стать: сдвиг запятой при перенесении информации из документа, занесение данных в другую графу и т.д.

Выявление, исключение таких значений, замена их истинными или расчетными — необходимый этап первичной обработки данных, так как применение математических методов к «засоренной» информации приводит к искажению результатов анализа. Однако аномальные значения могут отражать и реальное развитие процесса, например скачок курса доллара в «черный вторник», как правило, эти значения также заменяются расчетными при построении моделей, но учитываются при расчете возможных отклонений фактических значений от полученных по модели.

Соответствие исходной информации всем указанным требованиям проверяется на этапе предварительного анализа временных рядов. Лишь после этого переходят к расчету и анализу основных показателей динамики развития, построению моделей прогнозирования, получению прогнозных оценок.

В ходе предварительного анализа определяют, соответствуют ли имеющиеся данные требованиям, предъявляемым к ним математическими методами, строят график временного ряда, рассчитывают основные динамические характеристики, проверяют наличие тренда, сглаживают временной ряд.

График временного ряда дает общее представление о динамике изучаемого процесса. Современные программные средства предостав­ляют исследователю большие возможности по построению различных графиков, в том числе и временных рядов. Графически ряды динамики изображаются в основном либо линейными, либо столбиковыми диаграммами. По графику временного ряда можно сделать много выводов, в дальнейшем эти выводы могут быть проверены с помощью расчетов.

Визуальный анализ графиков временного ряда позволяет определить наличие тренда и его характер, наличие сезонных и циклических компонент. Выявление сезонных колебаний удобно производить по графику временного ряда, построенного методом наложения. В этом случае по оси абсцисс откладывается интервал времени предполагаемого периода колебаний, например, год, с разбивкой по месяцам. А по оси ординат - значения уровней ряда за несколько лет. Если во временном ряду имеются периодические изменения, то на графике наблюдаются пики или впадины в определенный период времени.

Выявление аномальных наблюдений является необходимой процедурой анализа временных рядов. Обычно аномальные значения уровней временного ряда можно обнаружить визуально по графику ряда, но прежде чем «подправить» обнаруженные таким образом значения ряда, их необходимо подвергнуть количественному и качественному анализу. Причинами аномальных значений уровней временного ряда могут быть ошибки, возникающие при измерении, передаче, агрегировании, дезагрегировании показателей, т. е. есть ошибки технического порядка. Их называют ошибками первого рода. Ошибки первого рода подлежат устранению.

Аномальные значения во временных рядах могут возникать из-за воздействия на экономический процесс факторов, имеющих объективный характер, но проявляющихся очень редко, эпизодически. Это ошибки второго рода, они устранению не подлежат.

Существует ряд критериев для выявления и устранения аномальных наблюдений во временных рядах. Рассмотрим метод Ирвина.

Предположим, что имеется временной ряд , где . В соответствии с методом Ирвина рассчитывается характеристика 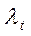по формуле:

; ,

где - среднеквадратическое отклонение, рассчитываемое по формуле:

, .

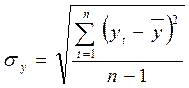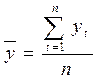Расчетные значения 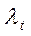сравниваются с табличным значением критерия Ирвина , значение которого зависит от количества членов временного ряда n и уровня значимости α (таб. 2.6.). Если расчетное значение 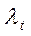больше табличного значения , соответствующее значение уровня ряда считается аномальным.

Таблица 2.6

n
α=0,05	2,8	2,2	1,5	1,3	1,2	1,1	1,0
α=0,01	3,7	2,9	2,0	1,8	1,7	1,6	1,5

После выявления аномальных значений уровней временного ряда необходимо установить причины их возникновения. Аномальные наблюдения первого рода подлежат устранению. Наиболее простой подход заключается в замене аномального наблюдения средней арифметической простой из двух соседних уровней ряда.

Пример 1.1.

Имеются данные о поступлении единого социального налога (ЕСН) в региональный бюджет за 24 месяца (таб. 2.7.). Требуется проверить наличие аномальных наблюдений по методу Ирвина.

Таблица 2.7

месяц	ЕСН, тыс. руб.	месяц	ЕСН, тыс. руб.
			414 123 408 899 382 538 421 251 427 532

Решение. На рис.2.1 приведен график поступлений ЕСН в бюджет. На рисунке мы видим, что отдельным наблюдениям соответствуют резкие выбросы.

Рис.2.1 Поступления ЕСН в бюджет (в тыс. руб.)

Расчеты выполним используя Мастер функций программы Excel (рис.2.2, 2.3).

Рис.2.2 Расчет среднего значения с помощью

статистической функции СРЗНАЧ

Рис. 2.3 Расчет среднего квадратического отклонения с помощью статистической функции СТАНДОТКЛОН

Результаты расчетов в Excel-таблицах:

.

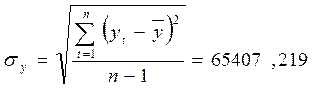Рис.2.4 Расчет величины 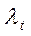для уровней временного ряда

Результаты расчетов приведены в таблице 2.8.

Таблица 2.8

месяц	ЕСН, тыс. руб.		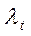месяц	ЕСН, тыс. руб.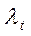
		- 2,49 1,04 0,31 0,03 0,06 1,11 0,58 0,01 0,24 0,15 0,24		414 123 408 899 382 538 421 251 427 532	2,46 4,15 1,64 0,48 0,15 0,15 0,39 0,00 0,08 0,40 0,59 0,10

Выберем , поскольку в таблице нет искомых значений для n=24 (ближайшие табличные значения параметров соответствуют n=20 и n=30), то необходимые нам данные находим приближенно с помощью интерполирования. Получим . Сравнивая с видим, что аномальными являются наблюдения 2,13,14,15.

Временные ряды, отображающие развитие экономического процесса, имеют, как правило, тенденцию к возрастанию или убыванию. По графику временного ряда можно определить наличие тенденции, но не всегда тенденция прослеживается достаточно четко. Поэтому прежде, чем перейти к определению тенденции и выделению тренда, необходимо выяснить, существует ли вообще тенденция во временном ряде.

В настоящее время существует большое количество методов, позволяющих определить наличие тенденции во временном ряду. Основные подходы к решению данной задачи основаны на статистической проверке гипотезы о случайности ряда. Рассмотрим некоторые из них.

Критерий серий, основанный на медиане. Проверяется гипотеза о неизменности среднего значения временного ряда:

Н₀ . (2.3)

Расположим члены анализируемого временного ряда в порядке возрастания и определим выборочную медиану Ме по формуле:

если n нечетно,   если n четно.

После этого по исходному временному ряду образуем «серии» из плюсов и минусов, на статисти­ческом анализе которых основана процедура проверки гипотезы (2.3). Рядом с каждым уровнем временного ряда , где , ставится знак «плюс», если , и «минус», если(уровни временного ряда, равныемедиане Ме,в полученной таким образом последовательности плюсов и минусов не учитываются).

Образованная последовательность плюсов и минусов характеризует­ся общим числом серий ν(n) и протяженностью самой длинной серии K_max. При этом под «серией» понимается последовательность подряд иду­щих плюсов и подряд идущих минусов. Если анализируемая после­довательность состоит из статистически независимых наблюдений, случайно варьирующих около некоторого постоянногоуровня, т. е. если справедлива гипотеза (2.3) о неизменности среднего уровня временного ряда, то чередование плюсов и минусов в постро­енной последовательности должно быть случайным, т.е. эта последовательность не должна содержать слишком длинных серий подряд идущих плюсов или подряд идущих мину­сов, и, соответственно, общее число серий ν(n) не должно быть слишком малым. Так что в данном критерии рассматривается одно­временно пара критических статистик: ν(n) и K_max. Поэтому, для того чтобы не была отвергнута гипотеза о неизменности среднего значения временного ряда должны одновременно выполняться два неравенства:

.

Квадратные скобки в неравенствах означают целую часть числа. Если хотя бы одно из неравенств нарушается, то гипотеза (2.3) отвергается с вероятностью ошибки α (0,05<α<0,0975), и тем самым подтверждается наличие зависящей от времени неслучайной составляющей в разложении анализируемого ряда: Y=U+S+E.

Пример 1.2. В таблице 2.9 представлена динамика стоимости акций РАО ЕЭС за период с декабря 2000 года по апрель 2003 года. Определить наличие тенденции во временном ряде с помощью критерия серий, основанного на медиане.

Таблица 2.9

Номер	Месяц	Стоимость, руб.	Номер	Месяц	Стоимость, руб.
	Декабрь 2000 Январь 2001 Февраль Март Апрель Май Июнь Июль Август Сентябрь Октябрь Ноябрь Декабрь Январь 2002 Февраль	2,27 3,02 2,75 2,87 3,08 3,03 3,29 3,17 3,17 2,59 2,91 4,31 4,47 4,98 4,63		Март Апрель Май Июнь Июль Август Сентябрь Октябрь Ноябрь Декабрь Январь 2003 Февраль Март Апрель	5,09 4,67 4,29 3,14 2,73 2,85 2,57 3,47 3,96 4,12 3,56 4,17 4,08 4,68

Решение. На рис. 2.5 представлен график динамика стоимости акций РАО ЕЭС за период с февраля 2001 года по апрель 2003 года.

Рис.2.5. Динамика стоимости акций РАО ЕЭС за период с февраля 2001 года по апрель 2003 года

По графику можно предположить, что во временном ряде присутствует тренд. Подтвердим наше предположение с помощью специального статистического критерия.

Расположим уровни анализируемого временного ряда в порядке возрастания:

2,27	2,57	2,59	2,73	2,75	2,85	2,87	2,91	3,02	3,03	3,08	3,14	3,17	3,17	3,29
3,47	3,56	3,96	4,08	4,12	4,17	4,29	4,31	4,63	4,67	4,68	4,74	4,98	5,09

В середине ранжированного ряда находится медианна: . Далее произведем сравнение каждого уровня временного ряда с медианой. Результат сравнения отмечаем «+» или «-». Образованные серии из плюсов и минусов для уровней исходного ряда представлены в таблице 2.10.

Таблица 2.10

Время	yt	«серии» из плюсов и минусов	Время	yt	«серии» из плюсов и минусов
	2,27 3,02 2,75 2,87 3,08 3,03 3,29 3,17 3,17 2,59 2,91 4,31 4,47 4,98 4,63	- - - - - -   - - - - + + + +		5,09 4,67 4,29 3,14 2,73 2,85 2,57 3,47 3,96 4,12 3,56 4,17 4,08 4,68	+ + + - - - - + + + + + + +

Образованная последовательность плюсов и минусов характеризует­ся общим числом серий ν(n) и протяженностью самой длинной серии K_max. Общее число серий ν(n)=4, протяженностью самой длинной серии K_max=10.

Расчетные значения для проверки гипотез равны , .

Неравенства и не выполняются, следовательно, гипотеза о неизменности среднего значения временного ряда отвергается, т.е. тренд во временном ряду есть.

Критерий «восходящих» и «нисходящих» серий. Этот крите­рий «улавливает» постепенное смещение среднего значения в исследуемом распределении не только монотон­ного, но и более общего, например периодического, характера.

Так же, как и в предыдущем критерии, исследуется последователь­ность знаков — плюсов и минусов, однако правила образования этой последовательности в данном критерии иные. Здесь происходит сравнение каждого последующего уровня исходного ряда с предыдущим уровнем. Если , то ставится знак «плюс», если , то «минус». Если два или несколько следующих друг за другом наблюдений равны между собой, то принимается во внимание только одно из них. Очевидно, последовательность подряд идущих плюсов будет соответствовать тогда возрастанию результатов наблюдения (восходящая серия), а последовательность минусов — их убыванию (нисходящая серия). Критерий осно­ван на том же соображении, что и предыдущий: если выборка случайна, то в образованной нами последовательности знаков общее число серий ν(n) не может быть слиш­ком малым, а протяженность серий K_max слишком большой.

При уровне значимости 0,05<α<0,0975 для того чтобы не была отвергнута нулевая гипотеза (2.3) должны одновременно выполняться два неравенства:

.

Величина K₀(n) определяется в зависимости от длины временного ряда n (таб. 2.11).

Таблица 2.11

n	n≤26	26<n≤153	153<n≤1770
K0(n)

Если хотя бы одно из неравенств нарушается, то гипотеза (2.3) отвергается, следовательно, подтверждается наличие зависящей от времени неслучайной составляющей.

Пример 1.3. Определить наличие тенденции во временном ряде, приведенном в примере 1.2, с помощью критерия «восходящих» и «нисходящих» серий.

По этому критерию сравнением каждый последующий уровень исходного ряда с предыдущим уровнем. Результат сравнения так же отмечаем «+» или «-». Образованные серии из плюсов и минусов для уровней исходного ряда представлены в таблице 1.11.

Таблица 2.12

Время	yt	«серии» из плюсов и минусов	Время	yt	«серии» из плюсов и минусов
	2,27 3,02 2,75 2,87 3,08 3,03 3,29 3,17 3,17 2,59 2,91 4,31 4,47 4,98 4,63	+ - + + - + -   - + + + + -		5,09 4,67 4,29 3,14 2,73 2,85 2,57 3,47 3,96 4,12 3,56 4,17 4,08 4,68	+ - - - - + - + + + - + - +

Общее число серий ν(n)=17, протяженностью самой длинной серии K_max=4.

Расчетные значения для проверки гипотез равны , .

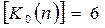Неравенства

выполняются, следовательно, гипотеза о неизменности среднего значения временного ряда подтверждается. Таким образом, на основании критерия «восходящих» и «нисходящих» серий делаем вывод, что тренд отсутствует.

Метод проверки разности средних уровней. По этому методу временной ряд разбивают на две примерно равные по числу уровней части (в первой части n₁ первых уровней исходного ряда, во второй остальные n₂ =n-n₁ уровней). Каждую из частей будем рассматривать как самостоятельную выборочную совокупность, имеющую нормальное распределение. Для каждой из этих частей вычисляются средние значения и дисперсии:

, ,

, .

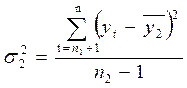Если временной ряд не имеет тенденции, то средние, вычисленные для каждой совокупности, не должны существенно различаться между собой. Таким образом, проверка наличия тренда в исследуемом ряду сводится к проверке гипотезы о равенстве средних двух нормально распределенных совокупностей

Н₀: .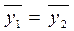

Предварительно проверяется дополнительная гипотеза о равенстве (однородности) дисперсий обоих частей ряда с помощью F- критерия Фишера. Расчетное значение F -критерия

если   если    

сравнивается с критическим (табличным) значением Фишера F_α с заданным уровнем значимости α (0,01<α<0,1) и числом степеней свободы ν₁ и ν₂ (ν₁ –число степеней свободы для большей дисперсии, ν₂ – число степеней свободы для меньшей дисперсии, число степеней свободы на 1 меньше числа наблюдений). Если расчетное значение F меньше табличного F_α, то гипотеза о равенстве дисперсий принимается и переходят к проверке равенства средних значений двух рядов. Если F -расчетное больше табличного F_α, то гипотеза о равенстве дисперсий отклоняется и делается вывод, что данный метод для определения наличия тренда не может быть применен.

Далее проверяется основная гипотеза с использованием t -критерия Стьюдента:

,

где s – среднее квадратическое отклонение разности средних, вычисляется на основе средней взвешенной величины дисперсий двух совокупностей:

Если расчетное значение t меньше табличного значения статистики с заданным уровнем значимости α, то нет оснований отвергать нулевую гипотезу о равенстве средних, т.е. тренда нет. В противном случае тренд есть. Заметим, что табличное значение t _α берется для числа степеней свободы равного (n₁ +n₂-2). Данный метод оказывается нечувствительным к небольшому тренду.

Пример 1.4. Определить наличие тенденции во временном ряде, приведенном в примере 1.2, с помощью критерия разности средних уровней.

Решение. Разделим исходный временной ряд на две примерно равные по числу уровней части: . Далее вычислим средние значения и дисперсии для каждой из частей:

,

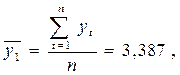
Проверим дополнительную гипотезу о равенстве (однородности) дисперсий обоих частей ряда с помощью F- критерия Фишера. Расчетное значение F -критерия:

.

Табличное значение F -критерия:

.

Так как , то с вероятностью 0,95 нет оснований отвергать гипотезу о равенстве дисперсий: выборочные дисперсии различаются незначимо.

Далее проверяем основную гипотезу о равенстве средних значений с использованием t -критерия Стьюдента. Расчетное значение t -критерия Стьюдента:

.

Табличное значение t -критерия Стьюдента можно получить, например, с помощью статистической функции Excel СТЬЮДРАСПОБР:

Так как , то основная гипотеза о равенстве средних в двух совокупностях не отвергается, расхождение между средними незначительное. Таким образом, на основании метода сравнения средних уровней делаем вывод, что тренд отсутствует.

Метод Фостера-Стьюарта. Этот метод дает более надежные результаты и обладает большими возможностями по сравнению с рассмотренными ранее. Кроме определения наличия тенденции процесса, метод Фостера-Стьюарта позволяет обнаружить тренд дисперсии временного ряда (если тренда дисперсии нет, то разброс уровней ряда постоянен, если дисперсия увеличивается, то ряд «раскачивается»), что важно знать при анализе и прогнозировании экономических процессов.

По этому методу проверка гипотезы об отсутствии во временном ряду тренда осуществляется при помощи двух вспомогательных величин d и s.

,

.

Значения и определяются путем последовательного сравнения уровней временного ряда:

	если больше всех предыдущих уровней; в противном случае,

	если меньше всех предыдущих уровней; в противном случае.

Величина s изменяется в пределах от 0 до n-1. Если все уровни равны, то s=0. Если уровни монотонно возрастают или убывают, то s= n-1.

Величина d изменяется в пределах от –(n-1) до n-1. Если d=–(n-1), то ряд монотонно убывает. Если d=n-1, то ряд монотонно возрастает. Кроме того, величина d может принимать нулевое значение в случаях:

- если все уровни равны между собой;

- если ряд в первой половине является монотонно убывающим, а во второй монотонно возрастающим;

- если уровни подъема и спада чередуются. Причем каждое следующее значение уровня подъема (спада) должно быть больше (меньше) всех предшествующих.

Перечисленные случаи, при которых d=0 представляют лишь теоретический интерес и вероятность их появления при проведении практических расчетов, особенно при исследовании экономических процессов крайне незначительна.

Обе величины s и d асимптотически нормальны и имеют независимые распределения. Показатель d применяетсядля обнаружения тенденций в средней, s – для обнаружения тенденций изменения дисперсии. Проверка гипотезы о том, можно ли считать случайными разности d-0 и s-µ проводится с использованием t -критерия Стьюдента:

, ,

, ,

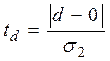где µ - математическое ожидание величины s, определенной для ряда, в котором уровни расположены случайным образом;

σ₁ – среднеквадратическое отклонение для величины s;

σ₂ – среднеквадратическое отклонение для величины d.

Значения величин µ, σ₁, σ₂ табулированы и приведены в таблице 2.13.

Таблица 2.13

n	µ	σ1	σ2	n	µ	σ1	σ2
	3,858 4,636 5,191 5,632 5,990 6,294 6,557 6,790 6,998 7,187	1,288 1,521 1,677 1,791 1,882 1,956 2,019 2,072 2,121 2,163	1,964 2,153 2,279 2,373 2,447 2,509 2,606 2,645 2,681		7,360 7,519 7,666 7,803 7,931 8,051 8,165 8,273 8,375	2,201 2,236 2,268 2,297 2,324 2,349 2,371 2,395 2,416	2,713 2,742 2,769 2,793 2,816 2,837 2,857 2,876 2,894

Расчетные значения t_d и t_s сравниваются с табличным значением t -критерия Стьюдента с заданным уровнем значимости t _α. Если расчетное значение меньше табличного, то гипотеза об отсутствии тренда в среднем и дисперсии принимается.

Пример 1.5. Определить наличие тенденции во временном ряде, приведенном в примере 1.2, с помощью метода Фостера-Стьюарта.

Решение. Последовательно сравнивая уровни временного ряда, заполняем таблицу:

Таблица 2.14

Время	yt					Время	yt
	2,27 3,02 2,75 2,87 3,08 3,03 3,29 3,17 3,17 2,59 2,91 4,31 4,47 4,98 4,63						5,09 4,67 4,29 3,14 2,73 2,85 2,57 3,47 3,96 4,12 3,56 4,17 4,08 4,68

На основании данных, приведенных в таблице, получим

, .

По таблице 1.13 с помощью интерполирования находим µ=5,918, σ₁ =1,864=, σ₂ =2,432, отсюда

, ,

Табличное значением t -критерия Стьюдента с уровнем значимости 0.05

.

Таким образом, гипотеза об отсутствии тенденции в среднем отклоняется, тренд во временном ряде есть. Гипотеза об отсутствии тенденции в дисперсии не отклоняется.

Одним из наиболее простых и распространенных методов выявления тенденции развития экономического процесса является сглаживание или выравнивание временного ряда. В ряде случаев общая тенденция отчетливо прослеживается в динамике показателя, в других – она может не просматриваться из-за значительных случайных колебаниях. Суть различных методов, с помощью которых производится сглаживание временных рядов, сводится к замене фактических уровней временного ряда расчетными, имеющими меньшую колеблемость, чем исходные данные.

Методы сглаживания делятся на две основные группы:

- выравнивание с применением кривой, проведенной между конкретными уровнями временного ряда таким образом, чтобы она отображала тенденцию, присущую ряду и одновременно освобождала его от незначительных колебаний;

- механическое выравнивание отдельных уровней временного ряда с использованием фактических соседних уровней.

Применение первой группы методов предполагает существование некоторой закономерности на протяжении всего временного ряда, либо его отдельных периодов. Параметры подобранной кривой остаются неизменными на протяжении всей отображаемой части ряда. В случае, когда для выравнивания временного ряда достаточно одной единственной кривой, то в дальнейшем эту кривую можно использовать при прогнозировании этого процесса в качестве кривых роста. Использование кривых для выравнивания временных рядов имеет определенные недостатки. Например, добавление к исходному ряду нового уровня по окончании месяца, квартала, года влечет за собой необходимость подбора новой выравнивающей кривой.

Суть методов механического сглаживания заключается в следующем. Берется несколько первых членов ряда, образующих так называемый интервал сглаживания. Для них подбирается кривая, аналитическим выражением которой служит полином, причем степень этого полинома должна быть меньше числа уровней, входящих в интервал сглаживания. С помощью полинома определяется новое выравненное значение уровня, находящегося в середине интервала сглаживания. Далее интервал сглаживания сдвигается на один член вправо, вычисляется следующее выравненное значение ряды, вновь производится сдвиг, потом вычисление и т.д. Для удобства вычисления и анализа число членов, составляющих интервал сглаживания, берется нечетным. В этом случае сглаженное значение ряда оказывается в центре интервала сглаживания и заменяет фактическое значение.

Самый простой из методов механического сглаживания – метод простой скользящей средней. Алгоритм сглаживания по простой скользящей средней состоит из следующих шагов:

1. Определить интервал сглаживания, т.е. число входящих в него уровней m (m<n), используя правило: если необходимо сгладить мелкие беспорядочные колебания, то интервал сглаживания берут по возможности большим и, наоборот, интервал сглаживания уменьшают, когда нужно сохранить более мелкие волны и освободиться от периодически повторяющихся колебаний.

2. Вычислить среднее значение уровней, образующих интервал сглаживания, которое одновременно является сглаживающим значением уровня, находящегося в центре сглаживания, при условии, что m нечетное число.

, t>p, (2.4)

где при нечетном m.

3. Сдвинуть интервал сглаживания на один уровень вправо, вычислить сглаженное значение по формуле (2.4) для t+1 уровня, снова произвести сдвиг и т.д. В результате последовательного применения приведенной итеративной процедуры получится n-(m-1) новых сглаженных уровней. Первые и последние p членов с помощью данного алгоритма сгладить нельзя, их значения теряются.

Пример 1.6. Имеются данные по выпуску продукции. Требуется сгладить временной ряд с помощью простой скользящей средней.

Решение. Результаты расчетов представлены в таблице 2.15. Экранные формы расчетов в Excel приведены на рис. 2.6. Результаты сглаживания по пятичленной скользящей средней показаны на рис. 2.7.

Таблица 2.15

Месяц	Выпуск продукции, тыс. руб	Скользящая средняя
трехчленная	пятичленная
			-	-
			(80+78+90)/3= =82,66667	-
			(78+90+87)/3= =85	(80+78+90+87+82)/5= =83,4
			(90+87+82)/3= =86,333	81,2
			79,333	80,2
			74,667	76,2
			70,667	72,6
			70,667	68,8
			67,333	67,2
			64,333	65,4
			62,667	64,8
				64,8
			66,667	64,8
			66,333	65,8
				65,2
			63,333

Рис. 2.6. Экранные формы расчетов в Excel

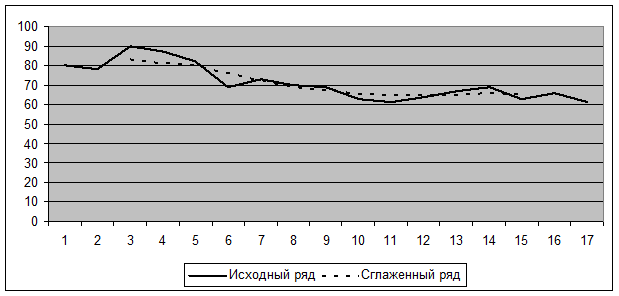
Рис. 2.7. Сглаженный временной ряд с помощью пятичленной скользящей средней

Метод простой скользящей средней применим, если графическое изображение динамического ряда напоминает прямую линию. В этом случае не искажается динамика развития исследуемого процесса. Однако когда тренд выравниваемого ряда имеет изгибы и к тому же желательно сохранить мелкие волны, использовать для сглаживания метод простой скользящей средней нецелесообразно, поскольку при этом: выравниваются и выпуклые и вогнутые линии, происходит сдвиг волны вдоль ряда, изменяется знак волны, т.е. на кривой, соединяющей сглаженные уровни, вместо выпуклого участка образуется вогнутый и наоборот. Последнее имеет место в тех случаях, когда интервал сглаживания в полтора раза превышает длину волны.

При нелинейном характере развития более надежным является использование других методов сглаживания, например метода взвешенной скользящей средней.

Если временной ряд содержит периодические колебания, то для устранения периодических колебаний интервал сглаживания должен быть равен периоду колебаний. Тогда для сглаживания сезонных колебаний с квартальной или годовой периодичностью рекомендуется использовать центрированную скользящую среднюю (пяти- или тринадцатичленную):

Пример 1.7. Имеются данные по денежной массе МО на начало периода, млрд.руб. Требуется сгладить временной ряд с помощью центрированной скользящей средней.

Месяц (на начало месяца, млрд.руб)
Январь	130,4	187,8	266,6
Февраль	116,4		232,9
Март	120,4	180,8
Апрель	119,1	174,1	251,5
Май	128,6	195,2	279,1
Июнь	129,9	205,3	289,3
Июль	129,8	216,4	321,8
Август	129,3	218,2
Сентябрь	133,4	216,2	341,6
Октябрь	154,2	212,8
Ноябрь	166,4		349,7
Декабрь	167,3	219,3	358,3

Решение. Экранные формы расчетов в Excel приведены на рис. 2.8. Результаты сглаживания по 13-членной скользящей средней показаны на рис. 2.9.

Рис. 2.8. Экранные формы расчетов в Excel. Сглаживание временного ряда с помощью 13-ти членной скользящей средней.

Рис.2.9. Сглаженный ряд динамики «Денежная масса» с помощью

13-ти членной скользящей средней.

Метод взвешенной скользящей средней. Взвешенная скользящая средняя отличается от простой скользящей средней тем, что уровни, входящие в интервал усреднения, суммируются с различными весам. Это связано с тем, что аппроксимация сглаживаемого временного ряда в пределах интервала сглаживания осуществляется с использованием уровней рассчитываемых по полиному не первой степени, как в предыдущем случае, а степени, начиная со второй. Следовательно, метод простой скользящей средней является частным случаем метода взвешенной скользящей средней.

Алгоритм метода взвешенной скользящей средней аналогичен алгоритму метода простой скользящей средней. Отличие его состоит в следующем:

1. На первом шаге, кроме интервала сглаживания, определяется и порядок аппроксимирующего полинома. Считается, что сглаживание временного ряда будет более «гибким» при использовании полиномов высоких степеней и при меньших размерах интервалов сглаживания. Более длинные интервалы сглаживания и невысокий порядок используемых полиномов позволяют избавиться от случайных отклонений и мелких волн.

2. В зависимости от степени полинома и длины интервала сглаживания для расчета сглаженных уровней используются приведенные ниже формулы:

Второй и третий порядок полинома:

m=5

m=7

m=9

Четвертый и пятый порядок полиномов:

m=7 m=9

m=11

В приведенных формулах веса уровней получены из условия, что сумма квадратов отклонений расчетных (сглаженных) значений уровней от фактических в интервале сглаживания минимальная. Из приведенных формул видно, что веса симметричны относительно центрального члена и сумма весов с учетом общего множителя равна единице. Заметим также, что в системе весов кроме положительных величин имеются и отрицательные. Это приводит к тому, что сглаженная кривая в значительной степени сохраняет различные изгибы кривой тренда.

Если полученные сглаженные уровни обладают все еще значительной колеблемостью, то процедуру сглаживания можно повторить.

Метод скользящих средних не дает возможности сгладить первые и последние p уровней временного ряда. Отсутствие сглаженных первых уровней не так важно по сравнению с последними уровнями, особенно, если целью исследования является прогнозирование развития процесса. Существуют методы, позволяющие путем дополнительных вычислений получить, хотя и с меньшей степенью устойчивости, значения тренда на концах временного ряда. Кроме того, существуют методы сглаживания, при использовании которых последние уровни сглаживаются так же, как и остальные. К их числу относится метод экспоненциального сглаживания.

Метод экспоненциального сглаживания. Особенность этого метода состоит в том, что в процедуре выравнивания каждого уровня используются только значения предыдущих уровней, взятых с определенным весом. Вес каждого наблюдения уменьшается по мере его удаления от уровня, для которого определяется сглаживаемое значение. Сглаженное значение уровня временного ряда s_t на момент t определяется по формуле

, (2.5)

где α – сглаживающий параметр, характеризующий вес выравниваемого уровня (0< α ≤.1).

Соответственно этой формуле сглаженное значение уровня ряда s_t на момент t времени представляется линейной комбинацией двух величин: фактического уровня y_t для этого же момента времени и сглаженного уровня для предыдущего момента s_t-1 . Величину s_t-1 в формуле (2.5) также можно представить в виде суммы фактического уровня y_t-1 и сглаженного уровня предшествующего ему уровня s_t-2, взятых с соответствующими весами. Процесс такого разложения можно продолжить для членов s_t-2, s_t-3 и т. Д. В результате получится следующее выражение:

, (2.6)

в котором среднее сглаженное значение представляет собой линейную комбинацию всех уровней от y₁ до y_t. Величина s₀ характеризует начальные условия процесса, сложив в формуле (1.4) все члены, содержащие параметр α получим:

, (2.7)

где j – число периодов отставания от момента времени t.

Согласно формуле (2.7) относительный вес каждого предшествующего уровня снижается по экспоненте по мере его удаления от момента, для которого имеется сглаженное значение. Отсюда и произошло название данного метода сглаживания.

При использовании метода экспоненциального сглаживания возникают определенные трудности при выборе сглаживающего параметра α и определении начальных условий s₀.

От численного значения параметра α зависит, насколько быстро будет уменьшаться вес предшествующих наблюдений и в соответствии с этим степень их влияния на сглаживающий уровень. Чем больше значение параметра α, тем меньше сказывается влияние предшествующих уровней и, соответственно, меньшим оказывается сглаживающее воздействие экспоненциальной средней.

В качестве параметра s₀, определяющего начальные условия, предлагают использовать либо первое значение уровня временного ряда y₁, либо среднюю арифметическую нескольких первых уровней ряда, например, уровней y₁, y₂, y₃,:

.

Дата добавления: 2014-10-22