При решении экономических задач

Применение определенного интеграла

Определенного интеграла

Вычисление объемов тел вращения с помощью

Пусть тело получено вращением криволинейной трапеции , , 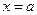, вокруг оси 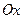. В этом случае поперечными сечениями будут круги с радиусами, равными , имеющими площадь .

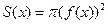Объем полученного тела вращения находится по формуле:

.

Например, найти объем тела, образованного вращением эллипса вокруг оси 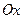. Так как эллипс симметричен относительно осей координат, то достаточно найти половину искомого объема. По формуле для нахождения объема тела вращения вокруг оси 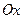имеем:

.

Тогда искомый объем 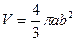(куб. ед. изм.).

Также можно найти с помощью определенного интеграла площадь поверхности указанного тела вращения по формуле:

.

Рассмотрим некоторые примеры приложений определенного интеграла в экономике.

Пример 1. Найти дневную выработку за восьмичасовой рабочий день, если производительность труда в течение дня менялась по формуле , где 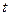– время в часах, – объем продукции, выпускаемой в час.

Решение. Предполагая, что производительность в течение рабочего дня меняется непрерывно от времени работы на отрезке [0, 8], дневную выработку 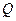можно выразить определенным интегралом:

В общем случае, если требуется по данной производительности труда вычислить количество произведенной продукции за время от до , применяют формулу:

.

Пример 2. Определить количество прибыли по данной отзывчивости производства 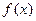, если инвестиции 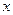изменяются в пределах от 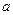до .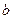

Решение. Отзывчивость производства на инвестиции есть производная от прибыли по вложенным средствам 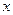, то есть , следовательно, . Интегрируя это равенство на отрезке , получим , .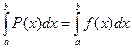

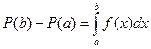Итак, при внесении инвестиций в пределах от 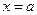до 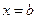количество прибыли равно определенному интегралу от отзывчивости производства на отрезке .

Пример 3. Пусть функция 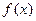указывает, какая х -я часть самых бедных людей общества владеет f (x)-й частью всего общественного богатства. Если бы распределение богатства было равномерным, то график функции 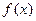шел бы по диагонали квадрата.

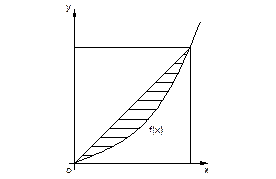
Чем больше площадь заштрихованной части, тем неравномерно распределено богатство в обществе. Величина этой площади называется коэффициентом Джинни.

Найти коэффициент Джинни распределения богатства в обществе, если функция .

Решение. Выполним чертеж

Коэффициент Джинни будет равен:

Дата добавления: 2014-11-26