
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Приклад. Матеріальна точка підвішена на стержні стиржні довжиною
|
|
|
|
Матеріальна точка підвішена на стержні стиржні довжиною 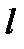 .
.
Рівняння в’язі має вигляд:
 .
.
В’язь називається односторонньою, якщо, обмеження координати точки що накладаються нею, виражаються в формі нерівностей. Одностороння в’язь обмежує переміщення точки лише в одному напрямку и і допускає її переміщення в інших напрямках.

| Рисунок 20.2 |
Матеріальна точка підвішена на нитці довжиною 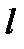 .
.
Рівняння в’язі має вигляд:
 .
.
Принцип звільнення від в’язей
В’язь можна відкинути замінивши дію в’язі силою реакції в’язі.:
 .
.
В У проекціях на осі декартової системи координат це буде виглядати такмати такий вигляд:
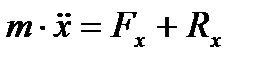 ,
,
 ,
,
 .
.
Відносний рух матеріальної точки
В У багатьох задачах динаміки рух матеріальної точки розглядається відносно системи відліку, що рухається відносно інерційної системи відліку.
Отримаємо диференціальні рівняння руху матеріальної точки відносно рухомої системи відліку.
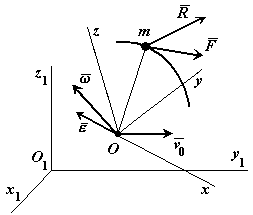
| Рисунок 20.3 |
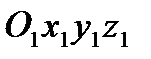 - – інерційна система відліку.
- – інерційна система відліку.
 - – рухома система відліку.
- – рухома система відліку.
 ,
,
де 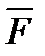 - – сума активних сил,
- – сума активних сил,  - – сума сил реакції в’язі.
- – сума сил реакції в’язі.
Згідно з теореми теоремою Коріоліса  .
.
Перепишемо диференціальні рівняння наступним таким чином:
 .
.
Введемо позначення:
 – переносна сила інерції,;
– переносна сила інерції,;
 – коріолісова сила інерції.
– коріолісова сила інерції.
З урахуванням цих позначень ми отримаємо динамічну теорему Коріоліса (рівняння відносного руху).
Матеріальна точка рухається відносно неінерційної системи відліку так, же само як і відносно інерційної, тільки до прикладених активних силам и і сил реакції в’язей слід додати коріолісову і переносну силу сили інерції.
 .
.
Сили  і
і  є поправками на не інерційність системи.
є поправками на не інерційність системи.
В У проекціях на рухомі осі:
 ,
,
 ,
,
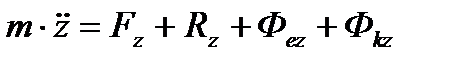 .
.
|
|
|
Окремі випадки відносного руху
1. Відносний рух за інерцією
Якщо матеріальна точка рухається відносно рухомої системи відліку прямолінійно і рівномірно, то такий рух називається відносним рухом за інерцією.
 ,
,  , як наслідок
, як наслідок
 .
.
2. Відносна рівновага
При спокої матеріальної точки відносно рухомої системи відліку її відносна швидкість і прискорення дорівнюють нулю, тобто
 і
і  , як наслідок, прискорення Коріоліса також дорівнює нулю
, як наслідок, прискорення Коріоліса також дорівнює нулю 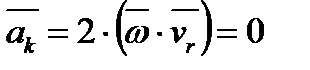 .
.
Умова відносної рівноваги має вигляд:
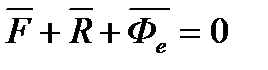 .
.
3. Інерційні системи відліку
Переносне прискорення в загальному випадку обчислюється за формулою
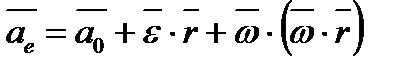 ,
,
де  - прискорення точки, прийнятої взятої за полюс (начало початок координат);
- прискорення точки, прийнятої взятої за полюс (начало початок координат); 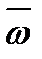 -кутова швидкість обертання рухомої системи координат довкола навколо обраного полюса;
-кутова швидкість обертання рухомої системи координат довкола навколо обраного полюса; 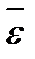 - – кутове прискорення цього обертання (
- – кутове прискорення цього обертання (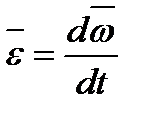 );
); 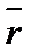 – радіус – вектор руху точки відносно полюса.
– радіус – вектор руху точки відносно полюса.
Якщо рухома система відліку рухається поступально, прямолінійно іта рівномірно, то
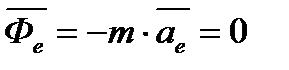 ,
, 
і рівняння відносного руху мають вигляд:
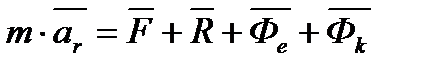 .
.
Рухома система відліку також інерційна.
Лекція 21
Короткий зміст: Внутрішні і та зовнішні сили. Центр мас. Моменти інерції відповідно відносно точки і осей. Теорема Штейнера.
Введення в динаміку системи
Механічною системою називається будь-яка система матеріальних точок і тіл.
Зовнішніми силами механічної системи називаються сили, з якими на точки і тіла механічної системи діють точки і тіла які не входять в дану систему.
Рівнодіюча Рівнодійна всіх зовнішніх сил, прикладених до першої точки, позначається  (від латинського exterior - – зовнішній).
(від латинського exterior - – зовнішній).
Внутрішніми силами механічної системи називаються сили взаємодії між точками і тілами даної системи.
Рівнодіюча Рівнодійна всіх внутрішніх сил, прикладених до першої точці точки, позначається 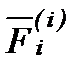 (від латинського interior - – внутрішній).
(від латинського interior - – внутрішній).
Цей поділ є умовним і залежить від того, яка механічна система розглядається.
|
|
|
Внутрішні сили системи володіють наступнимимають такі властивостямивластивості:
Теорема. Головний вектор всіх усіх внутрішніх сил системи (векторна сума) дорівнює нулю при будь-якому стані системи.:  .
.
Доведення:. Згідно з однією з аксіом динаміки, будь-які дві точки системи діють один на одного з рівними за величиною, але протилежно спрямованими силами. Векторна сума цих сил дорівнює нулю. Всі внутрішні сили є великою кількістю таких парних сил. Тому сума всіх внутрішніх сил дорівнює нулю.
Теорема. Головний момент всіх усіх внутрішніх сил системи (векторна сума) щодо будь-якої точки або осі дорівнює нулю при будь-якому стані системи.:
 або
або 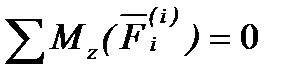 .
.
Доведення:Будь-які дві точки системи діють один на одного з рівними за величиною, але протилежно спрямованими силами. Сума моментів цих сил щодо будь-якої точки або осі дорівнює нулю. Всі внутрішня внутрішні сили є великою кількістю таких парних сил. Тому сума моментів всіх усіх внутрішніх сил відносно будь-якої точки або осі дорівнює нулю.
Диференціальні рівняння системи у векторній формі:
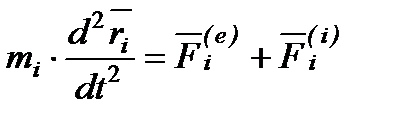 ,
,  .
.
Геометрія мас
Розглянемо механічну систему, яка складається з кінцевого числа 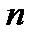 матеріальних точок з масами
матеріальних точок з масами  , а положення точок в у просторі задається радіусами-векторами
, а положення точок в у просторі задається радіусами-векторами  ., то
., то
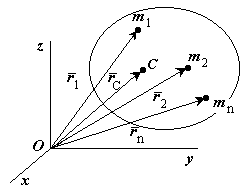
| Рисунок 21.1 |
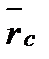 визначається виразом
визначається виразом

Деде 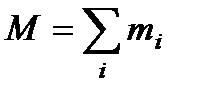 – маса системи.
– маса системи.
Якщо механічна система являє собою суцільне тіло, то його розбивають на елементарні частинки з нескінченно малими масами  . Суми в межі границях переходять в інтеграли, і центр мас визначається виразом
. Суми в межі границях переходять в інтеграли, і центр мас визначається виразом

Центр мас є не матеріальною точкою, а геометричноїгеометричною. Центр мас характеризує розподіл мас в у системі.
Координати центру центра мас мають вигляд:






Для тіл типу тонкого листа (поверхня) і тонкого дроту (лінія) 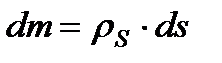 и та
и та 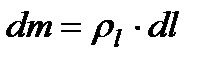 , де
, де  - – поверхнева і лінійна щільності відповідно. Інтеграли обчислюються по поверхні і та лінії.
- – поверхнева і лінійна щільності відповідно. Інтеграли обчислюються по поверхні і та лінії.
Моменти інерції для характеристики розподілу мас в у тілах при розгляді обертальних рухів вимагається ввести поняття Моменти моменти інерції.
Для характеристики розподілу мас в у тілах при розгляді обертальних рухів потрібно ввести поняття моментів інерції.
|
|
|
Момент інерції відносно точки є скалярна величина  або
або 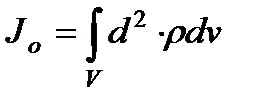
називається полярним моментом інерції відносно точки О. d – відстань від поточної точки до точки О.
Момент інерції щодо осі
Скалярна величина  або
або 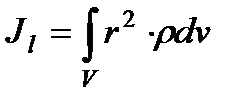
називається моментом інерції щодо відносно осі l. r – відстань від точки до осі.
Моменти інерції однакових за формою однорідних тіл, виготовлених з різних матеріалів, відрізняються один від одного. Характеристикою, не залежить від маси матеріалу, є радіус інерції.
Величина 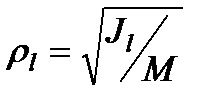 називається радіусом інерції.
називається радіусом інерції.
Момент інерції щодо відносно осі через радіус інерції щодо відносно цієї ж осі визначається виразом  .
.
Моменти інерції щодо відносно осей координат

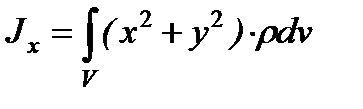 ,.
,.

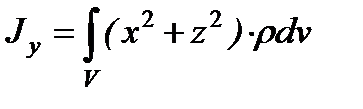 ,.
,.
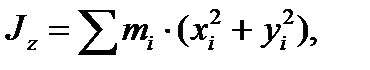
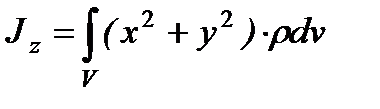 ,.
,.
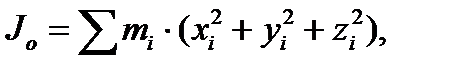
 ..
..
Відцентрові моменти інерції:
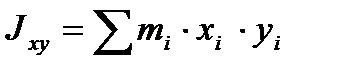 ,
,  ,.
,.
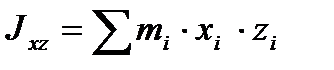 ,
,  ,.
,.
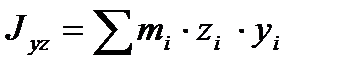 ,
, 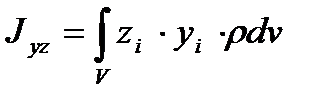 .
.
Встановимо Установимо залежність між моментами інерції паралельно осейосям, одна з яких проходить через центр мас.
Теорема про моменти інерції щодо паралельних осей. (Теорема Штейнера).
Момент інерції системи щодо відносно будь-якої осі дорівнює моменту інерції щодо відносно паралельної осі, що проходить через центр мас, плюс добуток маси системи на квадрат відстані між цими осями.
 .
.

| Рисунок 21.2 |
 та
та  , осі яких паралельні. Початок системи
, осі яких паралельні. Початок системи  знаходиться в центрі мас системи. Доведемо теорему для осей
знаходиться в центрі мас системи. Доведемо теорему для осей  и і
и і 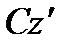 .
. 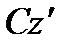 :
:

 .
.
Координати пов'язані між собою співвідношеннями:
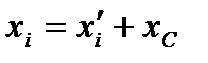 ,
,  ,
, 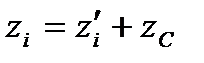 .
.

 ,
,  ,
, 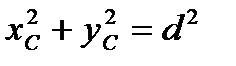 .
.
Отже,  , що потрібно було довести.
, що потрібно було довести.
Головними осями інерції називаються осі, в яких відцентрові моменти інерції дорівнюють нулю.
Моменти інерції тіла відносно головних осей інерції називаються
Гголовними моментами інерції тіла.
Тензор інерції и і тензор інерції для головних осей:

 .
.
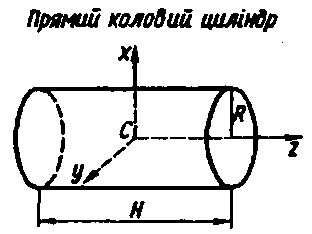
Моменти інерції найпростіших тіл
Таблиця 21.1
| Тіло | Момент інерції |

| 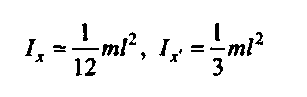
|

| 
|

| 
|

| 
|

| 
|
| 
|

| 
|

| 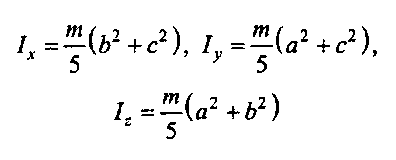
|

| 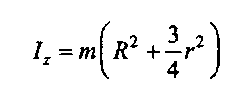
|
Лекція 22
Короткий зміст: Загальні теореми динаміки системи і твердого тіла:. Кількість руху системи. Теорема про зміну кількості руху системи. Закони збереження кількості руху. Теорема про рух центру центра мас. Момент кількості руху твердого тіла відносно осі обертання при обертальному русі твердого тіла. Момент кількості руху системи. Теорема про зміну моменту кількості руху системи. Закони збереження моменту кількості руху. Кінетична енергія системи. Кінетична енергія твердого тіла. Теорема про зміну кінетичної енергії системи.
|
|
|
Загальні теореми динаміки системи та твердого тіла
Кількість руху системи.
Кількістю руху системи матеріальних точок 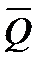 називається векторна сума кількостей рухів окремих точок системи.:
називається векторна сума кількостей рухів окремих точок системи.:
 .
.
Одиницею виміру кількості руху в СІ є - 
Кількість руху системи можна виразити через масу системи та швидкість центру центра мас.  .:
.: 
Теорема про зміну кількості руху системи.
Ця теорема існує в трьох різних формах.
Теорема. Похідна за часом від кількості руху системи дорівнює векторній сумі всіх зовнішніх сил, що діють на систему.:
 , ,
| (22.1) |
Доведення:. Теорема про зміну кількості руху для  точки має вигляд:
точки має вигляд:
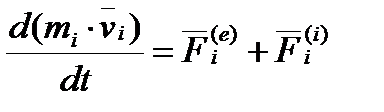 ,
, 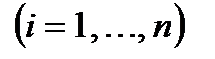 .
.
Складемо всі 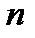 рівнянь і отримаємо:
рівнянь і отримаємо:  ,
,
Що що і потрібно було довести.
У проекціях на осі координат це твердження виглядає такмає такий вигляд:  ,
,  ,
, 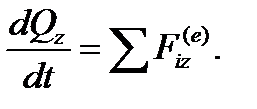 .
.
Теорема. (В У диференціальній формі). Диференціал від кількості руху системи дорівнює сумі елементарних імпульсів всіх усіх зовнішніх сил, що діють на систему.
Помножимо ліву і праву частини рівняння (22.1) на 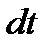 і одержимо
і одержимо
 , ,  . .
| (22.2) |
У проекціях на осі координат це твердження має такий вигляд:
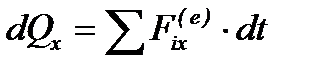 ,
, 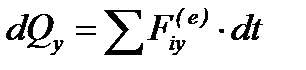 ,
, 
Теорема (в інтегральній формі). Зміна кількості руху системи за будь-який проміжок часу дорівнює векторній сумі елементарних імпульсів всіх зовнішніх сил, що діють на систему за цей же самий проміжок часу.
Інтегруючи обидві частини рівняння (22.2) за часом в межах від нуля до 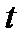 ,отримуємо:.
,отримуємо:.
У проекціях на осі координат це твердження має такий вигляд:
 ,
,  ,
, 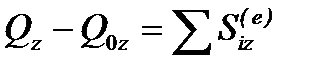 .
.
Закони збереження кількості руху.
1. Якщо головний вектор всіх усіх зовнішніх сил системи дорівнює нулю ( ), то кількість руху системи постійно постійна за величиною та напрямом.
), то кількість руху системи постійно постійна за величиною та напрямом.  :
: 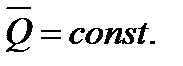
2. Якщо проекція головного вектора всіх зовнішніх сил системи на будь-яку вісь дорівнює нулю ( ), то проекція кількості руху системи на цю вісь є постійною величиною.
), то проекція кількості руху системи на цю вісь є постійною величиною. 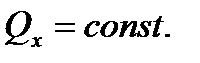
Теорема про рух центру центра мас.
Теорема. Центр мас системи рухається так само, як і матеріальна точка, маса якої дорівнює масі всієї системи, якщо на точку діють всі зовнішні сили, прикладені до розглянутої механічної системісистеми.:

 ,Отже
,Отже 
Момент кількості руху системи.
Моментом кількості руху системи матеріальних точок 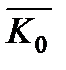 відносно деякого центру центра O називається векторна сума моментів кількості руху окремих точок цієї системи відносно того ж центру центра O:
відносно деякого центру центра O називається векторна сума моментів кількості руху окремих точок цієї системи відносно того ж центру центра O:

Моментом кількості руху системи матеріальних точок 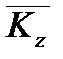 відносно якої-небудь осі
відносно якої-небудь осі  , що проходить через центр О, називається проекція вектора кількості руху
, що проходить через центр О, називається проекція вектора кількості руху 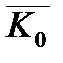 на цю вісь.
на цю вісь.  .:
.:  .
.
Момент кількості руху твердого тіла відносно осі обертання при обертальному русі твердого тіла.
Обчислимо момент кількості руху твердого тіла відносно осі обертання.:

| Рисунок 22.1 |



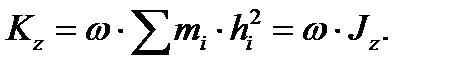
Момент кількості руху твердого тіла відносно осі обертання при обертальному русі дорівнює добутку кутової швидкості тіла на його момент інерції відносно осі обертання.:  .
.
Теорема про зміну моменту кількості руху системи.
Теорема. Похідна за часом від моменту кількості руху системи, взятого відносно якого-небудь центруцентра, дорівнює векторній сумі моментів зовнішніх сил, що діють на систему щодо відносно того ж центру.а:
 , ,
| (22.3) |
Доведення:. Теорема про зміну моменту кількості руху для  точки має вигляд:
точки має вигляд:
 ,
, 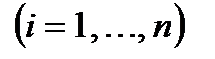 .
.
Складемо всі n рівнянь і отримаємо:
 або,
або,  ,що потрібно було довести.
,що потрібно було довести.
Теорема. Похідна за часом від моменту кількості руху системи, взятого відносно будь-якої осі, дорівнює векторній сумі моментів зовнішніх сил, що діють на систему відносно тієї ж осі.
Для доведення достатньо спроектувати векторне рівняння (22.3) на цю вісь. Для осі Oz це буде виглядати так:.виглядати так:
 ., .,
| (22.4) |
Теорема про зміну моменту кількості руху системи відносно центру центра мас. (Без без доведення)
Для осей, рухомих поступально разом із центром мас системи, теорема про зміну моменту кількості руху системи відносно центру центра мас зберігає той самий вигляд, що і відносно нерухомого центруцентра.
Закони збереження моменту кількості руху.
1. Якщо головний момент зовнішніх сил системи відносно точки О дорівнює нулю ( ), то момент кількості руху системи відносно точки О постійний за величиною і напрямком.
), то момент кількості руху системи відносно точки О постійний за величиною і напрямком.  :
: 
2. Якщо сума моментів усіх зовнішніх сил системи відносно якої-небудь осі дорівнює нулю( ), то момент кількості руху системи відносно цієї осі є постійною величиною.
), то момент кількості руху системи відносно цієї осі є постійною величиною.  :
: 
Кінетична енергія системи.
Кінетичною енергією системи називають суму кінетичних енергій всіх точок системи.:

Теорема Кеніга. Кінетична енергія системи в абсолютному русі складається з кінетичної енергії центру центра мас, якщо в ньому зосередити всю масу системи, і кінетичної енергії системи при її русі відносно центру центра мас.:
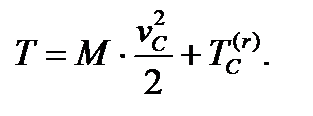
Доведення:. Розглянемо рух механічної системи відносно двох систем координат. Одна система нерухома, інша, з початком у центрі мас системи, переміщається щодо першої поступально.
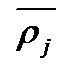 ,
,  , – Радіусрадіус-вектор і абсолютна швидкість
, – Радіусрадіус-вектор і абсолютна швидкість  точки відповідно;
точки відповідно;
 ,
, 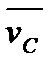 , – Радіусрадіус-вектор і абсолютна швидкість центру центра мас системи відповідно;
, – Радіусрадіус-вектор і абсолютна швидкість центру центра мас системи відповідно;
 ,
, 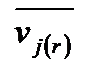 , – Радіусрадіус-вектор точки відносно центру центра мас і відносна швидкість цієї точки відповідно.
, – Радіусрадіус-вектор точки відносно центру центра мас і відносна швидкість цієї точки відповідно.
 ,
,  , (Так якОскільки переносний рух поступальний)
, (Так якОскільки переносний рух поступальний)

Так якОскільки,  , то
, то  або
або 

| Рисунок 22.2 |
Кінетична енергія твердого тіла.
1. Поступальний рух тіла.
Кінетична енергія твердого тіла при поступальному русі обчислюється так само, як і для однієї точки, у якій маса дорівнює масі цього тіла:.
 , – Швидкість швидкість будь-якої точки твердого тіла.
, – Швидкість швидкість будь-якої точки твердого тіла.
2. Обертання тіла навколо нерухомої осі.
Кінетична енергія твердого тіла при обертальному русі навколо нерухомої осі дорівнює половині добутку моменту інерції тіла відносно осі обертання на квадрат кутової швидкості тіла.
 ,
,  – Кутова кутова швидкість обертання твердого тіла.
– Кутова кутова швидкість обертання твердого тіла.
3.Плоский рух тіла.
Кінетична енергія твердого тіла при плоскому русі складається з кінетичної енергії тіла разом з центром мас і кінетичної енергії тіла від обертання навколо осі, що проходить через центр мас і перпендикулярній перпендикулярний площині руху.:.
 ,
,  – Швидкість швидкість центру центра мас твердого тіла,
– Швидкість швидкість центру центра мас твердого тіла,  - – кутова швидкість обертання твердого тіла.
- – кутова швидкість обертання твердого тіла.
Теорема про зміну кінетичної енергії системи.
Ця теорема існує у двох формах.
Теорема. Диференціал кінетичної енергії системи дорівнює сумі елементарних робіт всіх усіх зовнішніх і внутрішніх сил, що діють на систему.

Доведення: Теорема про зміну кінетичної енергії для  точки має вигляд:
точки має вигляд:
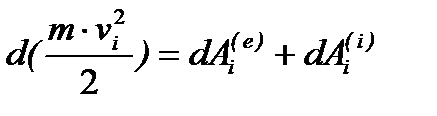 ,
, 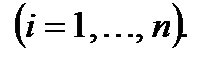
Складемо всі n рівнянь і отримаємо:
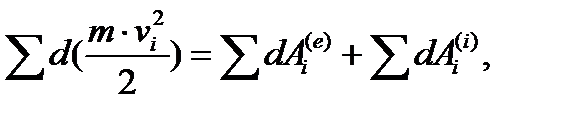
або 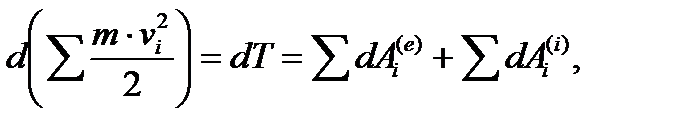
або  .
.
що і потрібно було довести.
Теорема. Зміна кінетичної енергії системи при її переміщенні з одного положення в інше дорівнює сумі робіт всіх усіх зовнішніх і внутрішніх сил, що діють на систему, на відповідних переміщеннях точок системи при тому ж переміщенні системи:

КОНСПЕКТ КУРС ЛЕКЦІЙ
З з дисципліни
"Теоретична механіка"
для студентів напряму підготовки
0902 «Інженерна механіка»
спеціальності
6.050502 «Інженерна механіка»
денної та заочної форми навчання
Укладачі О.В.Драч
Відповідальний за випуск Н.О. Сучко
Редактор Т.Г. Чернишова
Комп'ютерний набір та верстання М.В.Вегера
Підп. до друку 14.09.2012,поз., поз.
Формат 60х84 /16.Ум. друк. арк.9,3 Обл.-вид. арк. 3-6,6Папір офсетний. Гарнітура Times. Друк офс.
Ум. друк. арк.. Обл.-вид. арк.
Тираж 50 пр. Зам. № Собівартість вид.
Зам. № Собівартість видання грн. к.
Видавництво Видавець і виготовлювач
СумДУ при Сумськомуий державному державний університет,
вул. Римського-Корсакова, 2 м. Суми 40007і
40007, м. Суми, вул. Р.-Корсакова, 2
Свідоцтво про внесення суб'єкта видавничої справи до Державного реєстру
ДК № 2365 3062 від 0817.12.20052007.
МІНІСТЕРСТВО ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ
СУМСЬКИЙ ДЕРЖАВНИЙ УНІВЕРСИТЕТ
КОНОТОПСЬКИЙ ІНСТИТУТ
До друку та в світ
дозволяю на підставі
«Єдиних правил»,
п. 2.6.14
Заступник першого проректора –
Насальник організаційно-методичного
управління В.Б. Юскаєв
3352 МЕТОДИЧНІ ВКАЗІВКИ
до організації самостійної роботи студентів
із дисципліни
«Теоретична механіка»
для студентів спеціальності 6.050502
«Інженерна механіка» денної та заочної форми навчання
Усі цитати, цифровий та
фактичний матеріал, бібліографічні
відомості перевірені, запис одиниць
відповідає стандартам
Укладач: О.В. Драч
Відповідальний
за випуск О.Д. Динник
В.о. декана факультету
денної форми навчання Н.В. Барбара
Суми
Сумський державний університет
2012Надруковано у друкарні СумДУ
40007, м. Суми, вул. Р.-Корсакова, 2
|
|
|
|
|
Дата добавления: 2014-12-16; Просмотров: 1460; Нарушение авторских прав?; Мы поможем в написании вашей работы!