Генеральная и выборочная дисперсии

Отклонение от общей средней и его свойство.

Рассмотрим отклонение от общей средней и его свойство. Пусть дана совокупность (генеральная или выборочная) объема n:

хi			…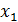
			…

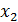
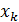
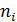
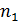
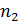
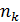
(далее для удобства записи будем использовать знак Σ). Найдем общую среднюю:

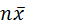, тогда = (1)

Так как 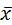– постоянная величина, то

(2)

Определение: Отклонением называется разность х_i – 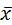между значением признака и общей средней.

Теорема: Сумма произведений отклонений на соответствующие частоты равна нулю: .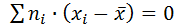

Доказательство: Учитывая формулы (1) и (2), имеем:

.

Что и требовалось доказать.

Следствие: Среднее значение отклонения равно нулю.

Действительно, 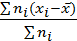= = 0.

Пример: Дано распределение количественного признака Х:

хi
ni

Убедимся, что сумма произведений отклонений на соответствующие частоты равна нулю.

Решение:

.

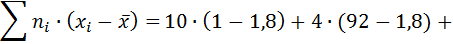
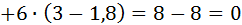Определение: Выборочной дисперсией 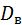называется среднее арифметическое квадратов отклонений значений признака выборочной совокупности от средней выборочной :

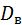= , если х_i различны

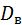или = средняя взвешенная квадратов отклонений с весами, равными соответствующим частотам.

Определение: Генеральной дисперсией D _г называют среднее арифметическое квадратов отклонений значений признака генеральной совокупности от генеральной средней :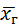

D _г= 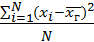, если х_i различны

или 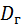= 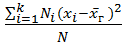– средняя взвешенная квадратов отклонений с весами, равными соответствующим частотам.

Пример: Генеральная совокупность задана таблицей распределения:

Xi
Ni

Найти D _г.

Решение: 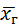= = 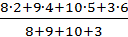4,

D _г = 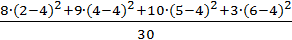= 1,8.

Определение: Выборочным средним квадратическим отклонением или стандартом называется квадратный корень из выборочной дисперсии

=

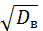
Определение: Генеральным средним квадратическим отклонением или стандартом называется квадратный корень из генеральной дисперсии

= .

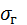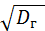Теорема: Дисперсия (генеральная или выборочная) равна средней квадратов значений признака минус квадрат общей средней

D = – .

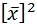Доказательство:

D = = = 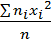- 2 +

+ = - 2 - = - .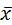

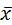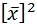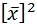Что и требовалось доказать.

Пример: Найти дисперсию по данному распределению.

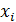
ni

Решение:

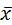= = 2

= = 5

D = - 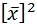= 5 - 2² = 1.

Определение: Коэффициентом вариации V называется выраженное в процентах отношение выборочного среднего квадратического отклонения к выборочной средней:

Он служит для сравнения величин рассеяния двух вариационных рядов. Ряд, у которого коэффициент вариации больше, имеет большее рассеяние.

5.5.Групповая, внутригрупповая, межгрупповая
и общая дисперсии.

Определение: Групповой дисперсией называют дисперсию значений признака, принадлежащих группе, относительно групповой средней:

= ,

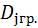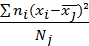где 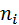– частота значения ;

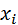j – номер группы;

=

Пример 1: Найти групповые дисперсии совокупности, состоящей из следующих двух групп:

Группа: №1 №2

Значение признака: 2, 4, 5 3, 8

Частота: 1, 7, 2 2, 3

Объем: 10 5

Решение: =

.

=

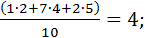
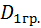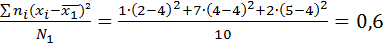
= = 6.

Определение: Внутригрупповой дисперсией называется средняя арифметическая групповых дисперсий, взвешенная по объемам групп:

= ,

где

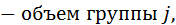
Пример 2: Найти внутригрупповую дисперсию по данным примера 1.

Решение: = .

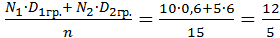Определение: Межгрупповой дисперсией называют дисперсию групповых средних относительно общей средней.

= ,

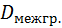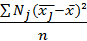где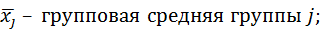

– объем группы ;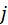

Пример 3: Найти межгрупповую дисперсию по данным примера 1.

Решение: ,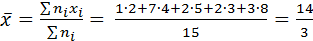

.

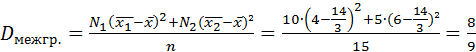Определение: Общей дисперсией называют дисперсию значений признака всей совокупности относительно общей средней:

= ,

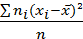где 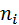– частота значения ;

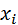Пример: Найти общую дисперсию по данным примера 1.

Решение: Найдем искомую общую дисперсию, учитывая, что общая средняя равна :

= .

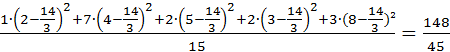Дата добавления: 2014-12-27