Исследований

Сначала рассмотрим основные законы распределения вероятностей дискретных случайных величин.

Определение: Говорят, что дискретная случайная величина Х распределена по биномиальному закону, если ее возможные значения представляют собой ряд целых неотрицательных чисел от 0 до n, а вероятности возможных значений определяются по формуле Бернулли, т.е.

,

где k – возможное значение случайной величины; n, p – некоторые постоянные (0< р <1, n ϵ N), называемые параметрами закона;

q = 1- p.

В этом случае табличный закон распределения случайной величины Х имеет вид:

X	0	1	2	…	k	…	n
P				…		…

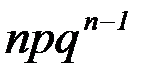
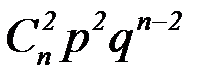
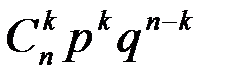
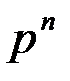
Название данного закона связано с тем, что значения вероятностей численно равны соответствующим членам разложения бинома Ньютона:

Класс биноминальных распределений обычно обозначается В(n,p).

Если Х В(n,p), то М(Х) = np, D(Х) = npq.

Пример: Монета брошена два раза. Написать закон распределения случайной величины Х – числа выпадений «орла», вычислить математическое ожидание и дисперсию.

Решение: Очевидно, что данная случайная величина имеет биномиальное распределение. Для вычисления вероятностей возможных значений Х применяем формулу Бернулли:

.

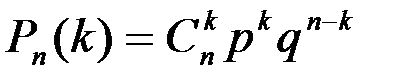Составим закон распределенияслучайной величины Х:

Х	0	1	2
Р

Математическое ожидание и дисперсию вычисляем по формулам: М(Х) = np, D(Х) = npq.

; .

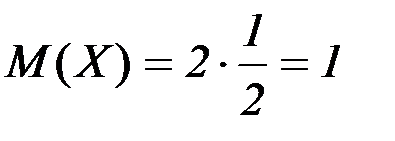Определение: Говорят, что дискретная случайная величина Х имеет геометрическое распределение, если ее возможные значения представляют собой ряд натуральных чисел, а вероятность возможного значения k вычисляется по формуле:

,

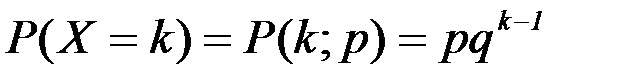где р – параметр закона (0< р <1); q = 1- p.

В этом случае табличный закон распределения случайной величины Х имеет вид:

X	1	2	3	…	k	…
P				…		…

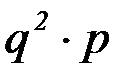
Класс геометрических распределений обычно обозначается G(p).

Если Х G(p), то , .

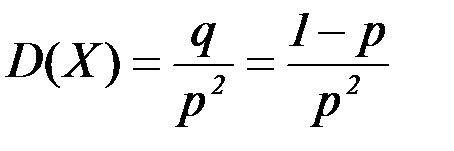Случайная величина, имеющая геометрическое распределение, возникает при описании числа испытаний до первого успеха (включая этот успех) в серии испытаний по схеме Бернулли. При этом р – вероятность успеха в отдельном испытании.

Заметим, что вероятности возможных значений данной случайной величины представляют собой члены убывающей геометрической прогрессии: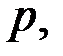

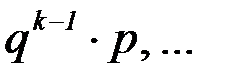
Применяя формулу суммы всех членов этой прогрессии, получаем, что сумма всех вероятностей случайной величины Х равна единице:

.

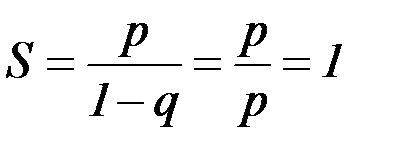Пример: Экзаменатор задает студенту дополнительные вопросы. Как только студент обнаруживает незнание вопроса, преподаватель ставит оценку. Вероятность ответить на любой дополнительный вопрос для студента равна 0,9. Составить закон распределения случайной величины Х – числа дополнительных вопросов, вычислить математическое ожидание и дисперсию.

Решение: Очевидно, что Х G(p), причем «успех» – это незнание вопроса. Следовательно, р = 1 - 0,9 = 0,1; q = 0,9.

Составим закон распределенияслучайной величины Х:

X	1	2	3	…	k	…
P				…		…

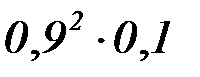
Применяя формулы для геометрического распределения, находим математическое ожидание и дисперсию:

; .

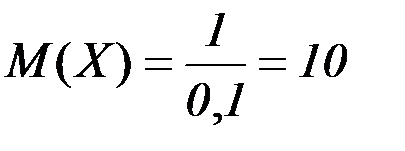Можно сделать вывод, что при данных условиях, среднее число дополнительных вопросов, заданных студенту равно 10.

Определение: Говорят, что дискретная случайная величина Х распределена по закону Пуассона, если ее возможными значениями могут быть только целые неотрицательные числа 0,1,…, k,… (последовательность этих значений теоретически не ограничена), а вероятность возможного значения k вычисляется по формуле Пуассона:

,

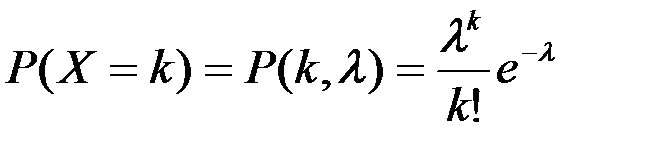где λ – параметр закона (λ > 0).

В этом случае табличный закон распределения случайной величины Х имеет вид:

X	0	1	2	…	k	…
P				…		…

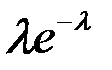
Причем сумма всех вероятностей представляет собой ряд, сходящийся к единице:

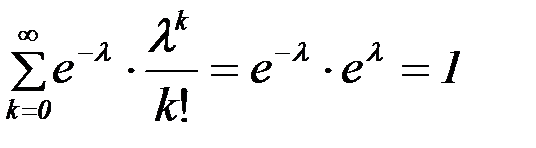
Класс распределения Пуассона обычно обозначается Р(λ).

Если Х Р(λ), то М(Х) = D(Х) = λ.

По закону Пуассона распределено, например, число вызовов на телефонной станции за фиксированный промежуток времени t, число отказов в работе радиоаппаратуры за время t, и так далее.

Это закон распределения вероятностей массовых (n велико) и редких (р мала) событий.

Определение: Говорят, что дискретная случайная величина Х имеет гипергеометрическое распределение, если ее возможными значениями являются целые неотрицательные числа 0, 1, 2, …, min (M, n), а вероятность возможного значения m вычисляется по формуле:

,

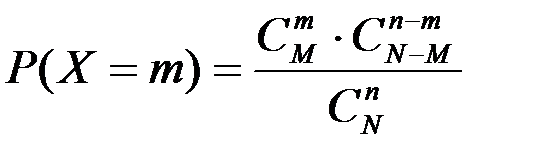где N, M, n – некоторые постоянные (параметры закона распределения); N, M, n N.

В этом случае табличный закон распределения случайной величины Х имеет вид:

X	0	1	2	…	m	…	n/M
P				…		…

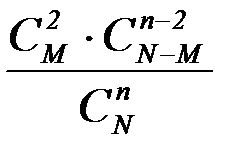
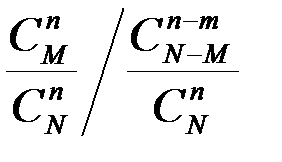
Заметим, что если n значительно меньше N (практически, если n < 0,1N), то гипергеометрическое распределение дает вероятности, близкие к вероятностям, найденным по биномиальному закону.

Случайная величина, имеющая гипергеометрическое распределение, возникает, например, при описании числа m стандартных изделий среди n отобранных из партии N изделий, среди которых М стандартных (М < N). Каждое изделие может быть извлечено с одинаковой вероятностью, причем отобранное изделие перед отбором следующего не возвращается в партию (поэтому формула Бернулли здесь неприменима).

Пример: Среди 50 изделий 20 окрашенных. Найти вероятность того, что среди наудачу извлеченных 5 изделий окажется ровно 3 окрашенных.

Решение: Из условия следует, что N = 50, M = 20, n = 5,

m = 3. По формуле для гипергеометрического распределения получаем:

.

Теперь рассмотрим основные законы распределения вероятностей непрерывных случайных величин.

Определение: Распределение вероятностей непрерывной случайной величины Х называют равномерным, если на промежутке, которому принадлежат все возможные значения этой случайной величины, плотность распределения вероятностей сохраняет постоянное значение.

Определение: Распределение вероятностей непрерывной случайной величины Х называют равномерным на отрезке [а;b], если его плотность выражается формулой:

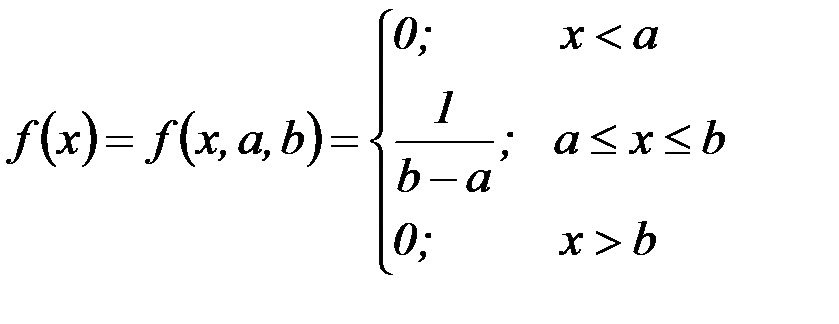
Класс равномерных распределений с параметрами a и b обычно обозначается R (a; b).

Функция равномерного распределения вероятностей на отрезке [ а;b ] задается формулой:

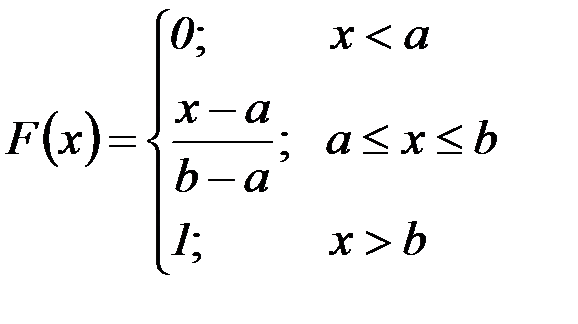
Построим графики плотности и функции распределения вероятностей для равномерно распределенной случайной величины Х:

f (x,a,b)

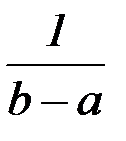
0 a b x

F(x,a,b)

1

0 a b x

Если случайная величина X ϵ R(a;b), то ее математическое ожидание и дисперсию можно вычислить по формулам:

;

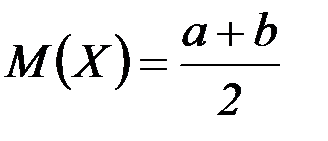Равномерному закону подчинены, например, ошибки округления.

Определение: Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины Х, которое описывается плотностью:

;

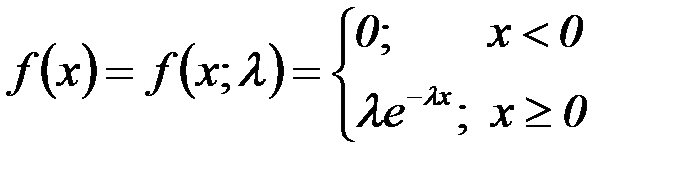где λ – постоянная положительная величина.

Функция показательного распределения вероятностей задается формулой:

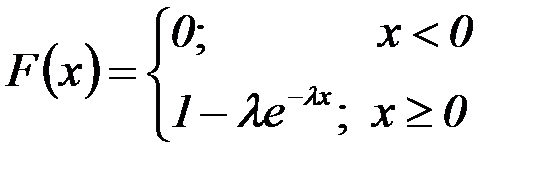
Построим графики плотности и функции распределения вероятностей для непрерывной случайной величины Х,распределенной по показательному закону:

f(x; λ )

λ

0 х

F(x)

1

0 х

Класс показательных распределений обозначается Е(λ). Если случайная величина X ϵ Е(λ), то ее математическое ожидание и дисперсию можно вычислить по формулам:

Примерами случайных величин, распределенных по показательному закону, служат: длительность телефонного разговора; время обслуживания заявки в системе массового обслуживания; длительность работы электронных ламп, полупроводниковых приборов и т.д. Поэтому показательный закон играет исключительную роль в теории надежности и в теории систем массового обслуживания.

Определение: Нормальным называется распределение вероятностей непрерывной случайной величины Х, которое описывается плотностью:

где а, σ – параметры распределения (а ϵ (-∞;+∞), σ > 0).

N(a,σ) – класс нормальных распределений.

Вероятностный смысл параметров:

а – математическое ожидание нормального распределения;

σ – среднее квадратическое отклонение нормального распределения.

Действительно, по определению математического ожидания получаем:

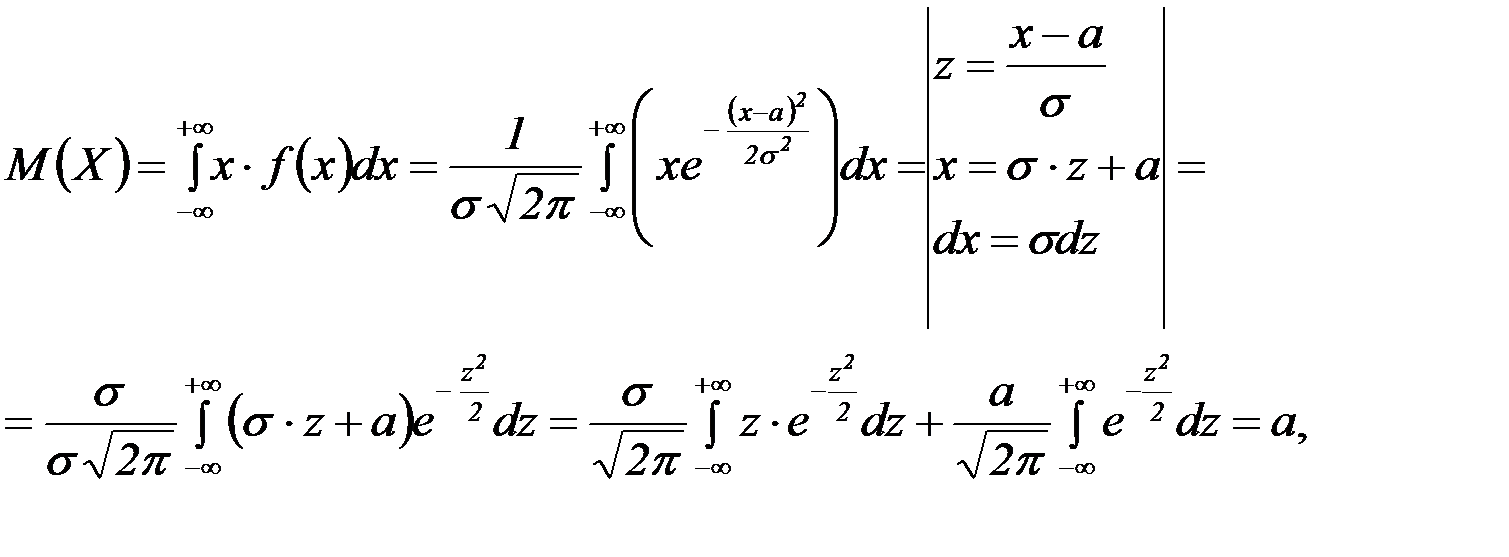
т.к. первое слагаемое равно нулю (под знаком интеграла нечетная функция, а пределы интегрирования симметричны относительно начала координат), второе слагаемое – интеграл Пуассона .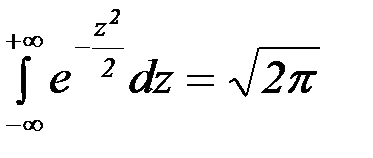

По определению дисперсии, учитывая, что М(Х) = а, имеем:

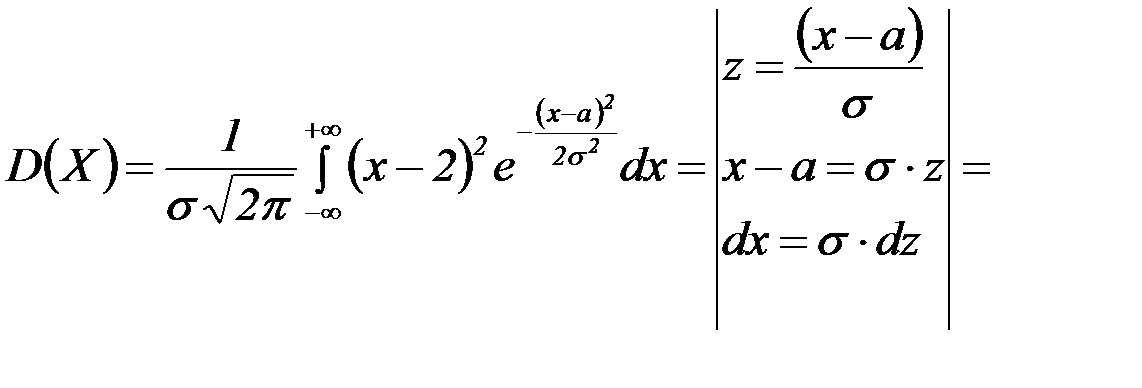
Определение: Общим называется нормальное распределение с произвольными параметрами а и σ (σ > 0).

Определение: Нормированным называется нормальное распределение с параметрами а = 0 и σ = 1.

Пример: Пусть Х – нормальная величина с параметрами а и σ. Тогда 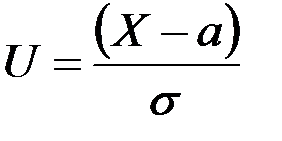– нормированная нормальная величина, M(U)=0, σ(U)=1.

Плотность нормированного распределения определяется формулой:

.

Функция F(x) общего нормального распределения определяется формулой:

,

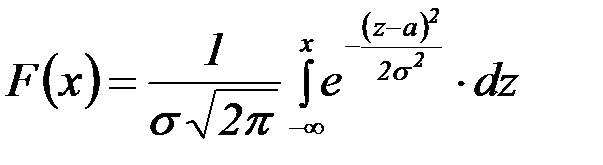а функция нормированного распределения имеет вид:

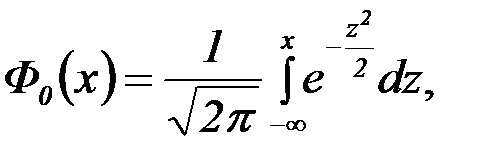
Заметим, что вероятность попадания нормированной нормальной величины Х в интервал (0; Х) можно найти, пользуясь интегральной функцией Лапласа:

Действительно,

Заметим, также, что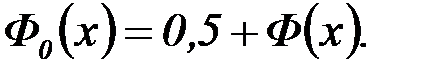

Действительно, φ(x) – четная функция. Пользуясь свойством плотности и определением функции распределения, получаем:

Определение: График плотности нормального распределения называется нормальной кривой (кривой Гаусса).

x

а

0

mаx

f(x)

График симметричен относительно прямой x = a.

При а = 0, σ = 1 нормальную кривую называют нормированной кривой.

Нормальная кривая имеет две точки перегиба:

.

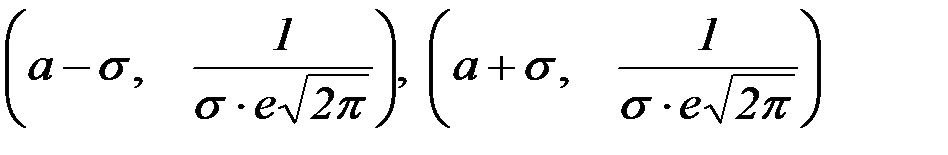Можно провести исследование функции методами дифференциального исчисления и убедиться в этом.

Заметим, что закон распределения нормальной случайной величины полностью определяется заданием а и σ. При изменении а график плотности не меняет своего вида, а лишь сдвигается влево или вправо. Поэтому а еще называют параметром сдвига.

Параметр σ – расстояние между точкой максимума и точкой перегиба. Поэтому говорят, что σ – мера «широты» кривой и называют параметром масштаба.

x

0

f(x)

σ =1

σ =3

σ =7

Дата добавления: 2014-12-27