Лекция 9. Предел функции

План:

1. Понятие предела функции.

2. Односторонние пределы.

3. Основные теоремы о пределах функции.

4. Техника вычисления пределов.

5. Предел функции на бесконечности

6. Замечательные пределы.

1. Понятие предела функции.

Пусть функция 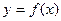определена в некоторой окрестности точки х_о, быть может, за исключением самой точки х_о.

Число b называется пределом функции 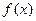при х, стремящемся к х_о (или в точке х_о), если для любого наперед заданного 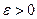существует такое 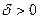, что для всех х, удовлетворяющих условиям 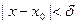, , 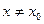имеет место неравенство: .

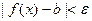Если b есть предел функци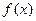и при 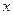→ 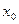то пишут: .

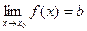Это определение предела функции называют определением предела по-Коши (или определением на языке ε-δ).

Приведем геометрическую иллюстрацию понятия предела функции в точке (рис. 9.1). Рассмотрим функцию .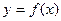

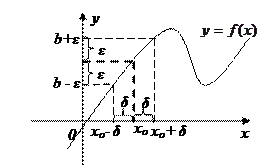Рис. 9.1.

A- ε

Предел функции b ищется по оси О у. Значение 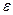выбирают близкое к нулю, это точность, с которой вычисляется данный предел. Чем меньше 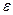, тем выше точность. Для любого 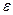можно подобрать такое число 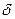, что если выбирать х из промежутка (х_о-δ; х_о+δ), то соответствующие значения 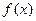будут принадлежать промежутку (b-ε; b+ε).

Другими словами, число b является пределом функци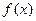и при 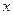→ 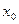, если для всех х, близких к х_о и отличных от х_о, соответствующие значения функции мало чем отличаются от числа b.

Отметим, что при нахождении предела значение функции в точке х_о может быть равно b, может отличаться от b, может не существовать.

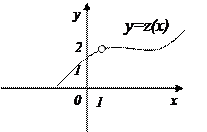Рассмотрим следующие примеры:

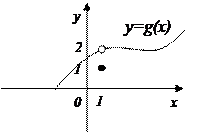
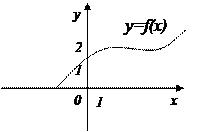
Рис. 9.2. Рис. 9.3. Рис. 9.4.

На рис. 9.2 функция определена в точке х_о= 1, причем 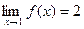(т.к. для всех х, близких к 1, соответствующие значения функции близки к 2).

На рис. 9.3 функция не определена в точке х_о= 1, но её предел в этой точке существует, причем 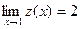. Это связано с тем, что при нахождении предела выбирают значения х, близкие к х_о, но отличные от х_о.

На рис. 9.4 функция определена в точке х_о= 1, но ее значение в точке не совпадает со значением предела: , а g (1)=1.

1. Односторонние пределы.

Если при нахождении предела функции выбирать значения переменной х только слева от точки х_о, то такой предел называется левосторонним и обозначается .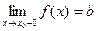

Если при нахождении предела функции выбирать значения переменной х только справа от точки х_о, то такой предел называется правосторонним и обозначается .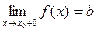

Левосторонний и правосторонний пределы могут совпадать, а могут отличаться друг от друга. Рассмотрим функци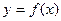и и 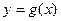, графики которых представлены на рис. 9.5 и 9.6. Найдем левосторонний и правосторонний пределы этих функций в точке х_о= 1.

Рис. 9.5.

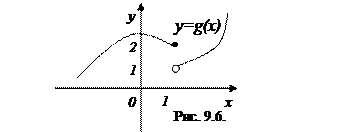
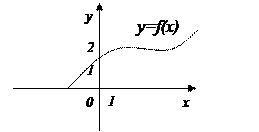
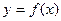
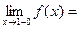
Для функции 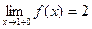, т.е. левосторонний и правосторонний пределы равны.

Для функции 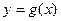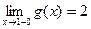, а 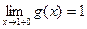, т.е. левосторонний и правосторонний пределы различны.

Функция имеет в точке единый предел тогда и только тогда, когда в этой точке существуют как правосторонний, так и левосторонний пределы, и они равны.

Так, функция на рис. 9.6 не имеет предела в точке х_о =1, поскольку левосторонний и правосторонний пределы функции в этой точке различны.

1. Основные теоремы о пределах функции.

Приведём без доказательства следующие теоремы о пределах функции.

Теорема 1. Функцию 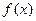, стоящую под знаком предела 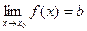, можно представить в виде: 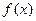= b+α(х), где α(х) – бесконечно малая функция при 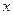→ 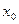(т.е. ).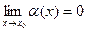

Теорема 2 (о пределах суммы, произведения и частного). Если функци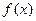и и 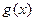определены в некоторой окрестности точки х_о и существуют пределы 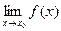, , 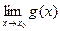то существуют пределы их суммы 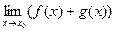, произведения 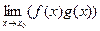и, если 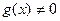, , 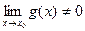то и частного 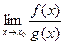и имеют место равенства:

1. ;

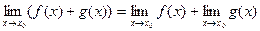2. ;

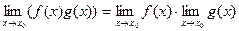3. 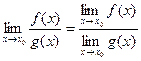, при , .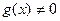

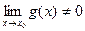Отметим некоторые следствия из теоремы 2.

1. Постоянный множитель может быть вынесен из-под знака предела.

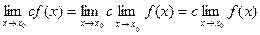(поскольку );

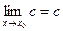1. Предел разности равен разности пределов.

;

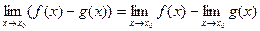1. Предел степени равен степени предела.

.

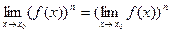Рассмотрим, как данные теоремы применяются при нахождении предела функции в точке.

Пример 9.1. Вычислите: .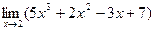

Решение. Используя теорему 2.1 и следствие 2, получаем, что предел суммы и разности равен сумме и разности соответствующих пределов:

.

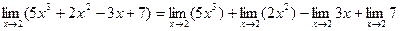В силу следствия 1, постоянный множитель может быть вынесен за знак предела: = .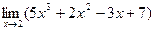

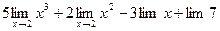В силу следствия 3, предел степени равен степени предела:

=

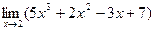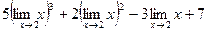
По определению 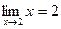, следовательно,

= .

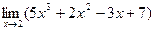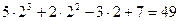Ответ: 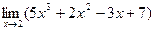=49.

Таким образом, для вычисления предела многочлена при 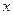→ 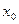достаточно вместо переменной х подставить значение х_о и выполнить соответствующие действия, т.е. .

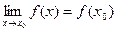Пример 9.2. Вычислите: .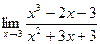

Решение. Чтобы применить теорему 2.3 о пределе частного 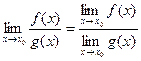, проверим выполнение следующих условий: 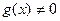, 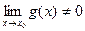. Поскольку 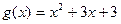, найдем 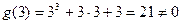и предел многочлена : .

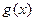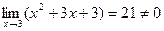Применим теорему 2.3: .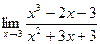

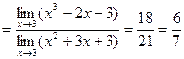Ответ: = .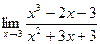

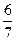Дата добавления: 2014-12-27