
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
ФУНКЦИИ. Одно из основных понятий математики – функция возникло при изучении явлений природы и решении различных практических задач
|
|
|
|
Одно из основных понятий математики – функция возникло при изучении явлений природы и решении различных практических задач. Изменение одних величин или данных вызывало изменение других, – например, изменение стороны квадрата приводит к изменению его площади, изменение скорости движения вызывает изменение пройденного расстояния. Обобщая аналогичные примеры можно дать общее понятие функции.
Определение. Функцией называется правило (соответствие), согласно которому изменение одной величины (например, х) вызывает изменение другой величины (например, у). Записывают это так: y=f(x). Здесь х – независимая изменяющаяся величина (аргумент), у – величина, которая изменяется при варьировании аргумента х. f – правило, в соответствии с которым происходит данное изменение. Задают функции одним из следующих способов:
1. Табличное задание функции. Строят таблицу соответствия между аргументами х и соответствующими значениями у. Наиболее часто такие таблицы строят при наблюдениях за каким – либо процессом, измерением, и т.д.
X X1 X2 X3.... Xn
Y Y1 Y2 Y3... Yn
табл 1
Недостатком такого способа задания функции является достаточно большой обьём информации и отсутствие наглядности.
2. Аналитическое задание функции, т.е. с помощью формулы у=f(х), например:
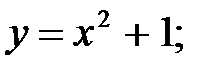
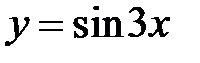 .
.
При таком способе задания в формулу закладывается алгоритм, который необходимо проделать с аргументом х для получения значения у. Этот способ задания является наиболее приемлемым при математических исследованиях.
3. Графический способ задания. На плоскости в декартовой системе координат изображается график функции (рис 3), т.е. множество точек(x,y) координаты которых удовлетворяют соотношению у=f(х). Такой способ задания является наиболее наглядным и позволяет быстро оценить характер поведения функции. Для дальнейшего изложения необходимо напомнить некоторые понятия, связанные с множеством вещественных чисел.
Интервалом (открытым промежутком) называют множество действительных чисел х удовлетворяющих неравенству a<x<b,или xЄ(a,b).
Отрезком (сегментом, замкнутым промежутком)называется множество точек (действительных чисел)удовлетворяющих неравенству a £ x £ b, или x Є [a,b],точки a и b в этом случае называют концами отрезка. По аналогии
определяются полуоткрытые интервалы:
a £ x < b, или x Є [a,b);
Y=f(x) a < x £ b, или x Є (a,b];
а также бесконечные
интервалы:
x (-¥,a)ó -¥ < x < a,
[b,¥)ó b £ x < ¥.
Рис 3
Интервал, (a,b) содержащий внутри себя данную точку х называется окрестностью этой точки. Если х является серединой интервала, то такая окрестность называется e – окрестностью точки х, где e =(b-a)/2.
На рис 4 изображена e - окрестность точки x.
x-e x x+e
рис 4
Областью определения функции y=f(x) называют множество вещественных чисел, для которых эта функция определена.
Областью изменения функции y=f(x) называют множество вещественных чисел, которые может принимать данная функция.
Упражнения. Найти область определения следующих функций:
1.y= 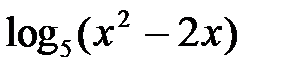 ; 2.y=
; 2.y= 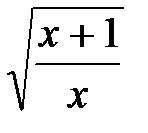 3.y=
3.y= 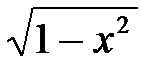

Ответы. 1. 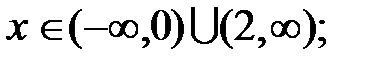 2.
2. 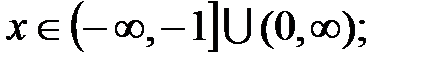 3.
3. 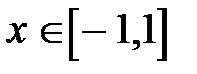 .
.
Рассмотрим некоторые классы функций, важные для дальнейшего.
1. Четные функции. Функция y=f(x), определенная на симметричном относительно х=0 множестве D, называется четной, если 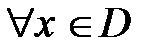
 выполняется условие f(-x)=f(x). Примерами четных функций могут служить следующие:
выполняется условие f(-x)=f(x). Примерами четных функций могут служить следующие:
y= 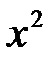 , y=
, y= 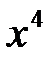 , y=cosx, y=
, y=cosx, y= 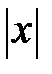 .
.
График любой четной функции симметричен относительно оси oy, в чем легко убедится из определения и рисунка 5.
2. Нечетные функции. Функция y=f(x) называется нечетной, если она определена на симметричном относительно х=0 интервале D и 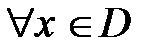 выполняется условие
выполняется условие
f(-x)= - f(x). Примерами таких функций могут служить y=x, y=x3,y=sinx.График любой нечетной функции симметричен относительно точки х=0, что легко проверить по
рисунку 6.
| х |
| y |
| x |
| y |
| F(x) |
| F(-x) |
| F(x) |
| F(-x) |
Рис 5 Рис 6
3. Периодические функции. Функция Y=f(x) называется периодической, если 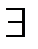 число T>0 такое, что f(x + T)=f(x).
число T>0 такое, что f(x + T)=f(x).
Наименьшее из чисел T называется периодом. Периодическими являются
функции y=sinx, y=cosx, y=tgx.Периоды их соответственно 2 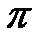 ,2
,2 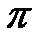 ,
, 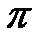 .
.
4. Монотонные функции. Функция y=f(x) называется возрастающей на интервале (a,b), если большему значению х соответствует большее значение y,т.е. если x2>x1 => f(x2) > f(x1). Аналогично функция называется убывающей на интервале, если большему значению х соответствует меньшее значение y, т.е. если x2>x1 => f(x2)<f(x1) (рис 7).
Если функция y=f(x) является
убывающей или возрастающей на
некотором интервале, то она
называется монотонной на этом
интервале.
возрастающая убывающая
Рис 7.
Упражнение. Определить, является ли функция четной или нечетной.
1.y=x2+1; 2. y=x3+2x; 3. y=x*cosx; 4.y=(x+1)/x; 5.y=log2x.
Ответ. 1-четная;2,3-нечетные;4 и 5 не являются ни четными, ни нечетными.
ПРЕДЕЛ ФУНКЦИИ
Последовательность (an), рассмотренная в предыдущем параграфе является частным случаем задания функции, а именно, можно полагать, что задана функция y=f(x) для целых значений аргумента х = 1,2,3…n,… в которых она принимает значения a1,a2,a3, …an …
Понятие предела последовательности также является частным случаем понятия предела функции в точке, к которому мы и переходим.
Определение. Число 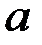 является пределом функции y=f(x) при x®x0, если для произвольного (сколь угодно малого) числа e >0 существует такое d>0 зависящее от e, что для всех точек х из d окрестности х0 (за исключением быть может самой точки х0) будет выполняться неравенство
является пределом функции y=f(x) при x®x0, если для произвольного (сколь угодно малого) числа e >0 существует такое d>0 зависящее от e, что для всех точек х из d окрестности х0 (за исключением быть может самой точки х0) будет выполняться неравенство 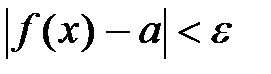 .
.
Используя символы математической логики можно это определение записать так:
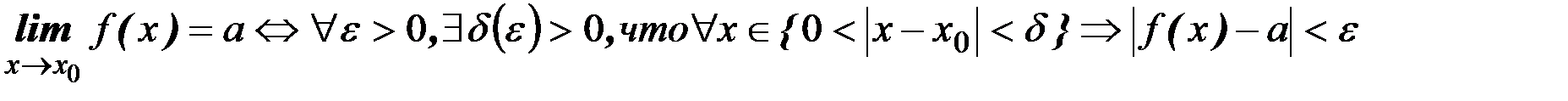
|
Геометрически это определение можно проиллюстрировать следующим образом. Рассмотрим график функции Y0=f(x) и точку х=х0 (Рис 8).Выберем
произвольное e>0 и окружим точку y=a e-окрестностью. Проведем прямые, параллельные ОХ через точки 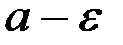 и
и 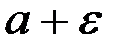 до пересечения с графиком y=f(x). Спроецируем полученные точки на ось ОХ. Все точки х, попавшие в заштрихованный интервал, судя по рисунку удовлетворяют соотношению
до пересечения с графиком y=f(x). Спроецируем полученные точки на ось ОХ. Все точки х, попавшие в заштрихованный интервал, судя по рисунку удовлетворяют соотношению 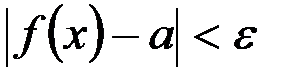
| х |
| y |
a+ 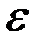 y=a
a-
y=a
a- 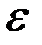
|
| x=x0 |
Рис.8
Выбрав произвольную d - окрестность в этом интервале, получим искомое число d(e).
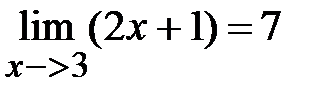
|
Выберем произвольное e >0 и рассмотрим абсолютную величину разности 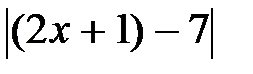 <e. Это неравенство эквивалентно двойному неравенству.
<e. Это неравенство эквивалентно двойному неравенству.
6-e<2x<6+e=> 3-e/2<x<3+e/2=> xÎ (3-e/2,3+e/2). Т.о. в качестве числа d(e) можно взять d(e)=e/2: тогда " х Î(3-e/2,3+e/2) значения функции y=2x+1 будут отличаться при х®1 от значения y=7 меньше чем на e.
Отметим здесь, что при определении предела функции в точке запись
x®x0 означает, что х приближается к точке х0 или слева или справа. Если выделить эти два случая отдельно, то получим определение предела слева или предела функции справа (односторонние пределы).
Обозначаются эти пределы соответственно так:
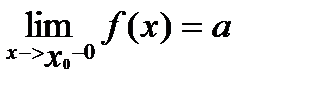
|
- предел функции f(х) в точке х0 слева,
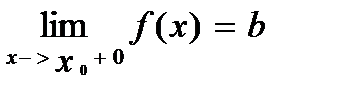
|
- предел функции f(х) в точке х0 справа.
Записи х®х0 -0 и х®х0+0 имеют символическое значение:
х®х0-0 означает, что х®х0 и при этом х<х0
х®х0+0 означает, что х®х0 и х>х0
Вычислим односторонние пределы для функции в точке х=1
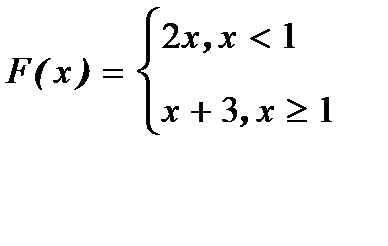
|
Предел слева:
 =(здесь мы воспользовались тем, что при х<1 значения функции вычисляются с помощью верхней строчки)=2.
=(здесь мы воспользовались тем, что при х<1 значения функции вычисляются с помощью верхней строчки)=2.
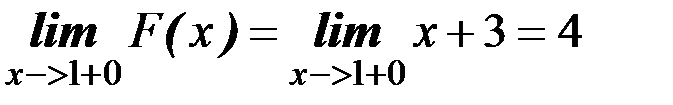
|
Нарисуем график этой функции (Рис 9). Стрелка на левой ветви графика
означает, что значение y=2 при х®1-0
не достигается. Точка на правой ветви
4 означает, что значение y=4 при х®1+0
2 достигается.
Утверждение. Если для функции y=f(x)
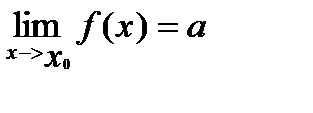
|
Рис 9.
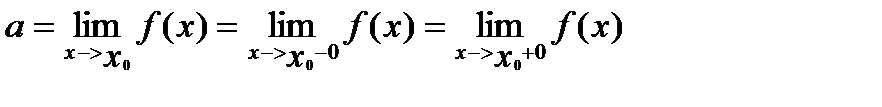
|
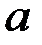 :
:
Обратно: если существуют односторонние пределы функции f(x) в точке х=х0 и они равны, то существует и:
ПРЕДЕЛ ФУНКЦИИ ПРИ 
Приведем определение предела функции при x®¥, предполагая при этом, что область определения функции не ограничена справа.
Определение. Число 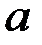 называется пределом функции y=f(x) при x®+¥ если для любого e >0 существует число N=N(e), такое, что при всех
называется пределом функции y=f(x) при x®+¥ если для любого e >0 существует число N=N(e), такое, что при всех
х >N(e) выполняется неравенство 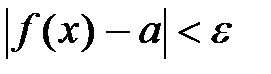
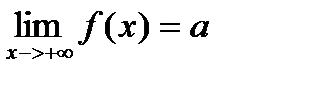
|
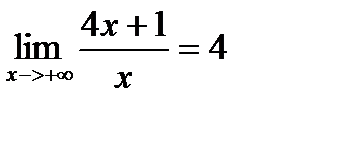
|
Пример: Доказать, что:
Решение: Выберем произвольное e>0. Рассмотрим разность 
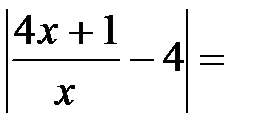
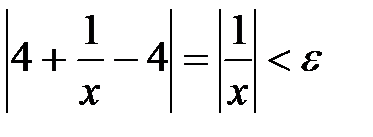 .Решая это неравенство относительно x, получим x >1/e. Полагая в определении предела число N(e) равным 1/e, имеем, что для всех х>N(e) выполняется неравенство
.Решая это неравенство относительно x, получим x >1/e. Полагая в определении предела число N(e) равным 1/e, имеем, что для всех х>N(e) выполняется неравенство 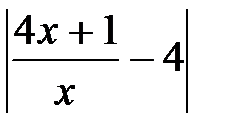 <e.
<e.
|
|
|
|
|
Дата добавления: 2014-12-23; Просмотров: 424; Нарушение авторских прав?; Мы поможем в написании вашей работы!