Бесконечно малые и бесконечно большие величины

Определение. Функция f(x) называется бесконечно малой при x®x₀ или при x®¥, если:

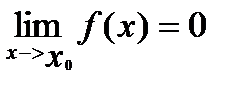
Так, например, функции y=1/x, (x+1)/x², sinx/x являются бесконечно- малыми при x®∞;

Функции y=(x-1)cos x, y=(x²-1)/(x+2) являются бесконечно малыми при

x®1.

По аналогии можно дать определение бесконечно малой любой переменной величины a:

Переменная величина a называется бесконечно малой, если lima=0.

Определение. Переменная величина b называется бесконечно-большой, если обратная к ней величина 1/a является бесконечно малой.

Например, функции y=1/x, (x+1)/x², являются бесконечно-большими при x®0, т.к. функции y=x, x²/(x+1) являются бесконечно малыми при x®0.

Важность введенного понятия бесконечно малой величины объясняется следующим утверждением о связи бесконечно малой величины и предела.

Утверждение. Функция y=f(x) имеет предел a при x®x₀, тогда и только тогда, когда ее можно представить в виде f(x)= a +a(x), где a(x) бесконечно-малая при x®x₀.

ОСНОВНЫЕ СВОЙСТВА ПРЕДЕЛОВ. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ

Основные свойства пределов функций совпадают со свойствами пределов последовательностей. Справедливы утверждения: если существуют конечные пределы функций f(x) и g(x):

то существуют и конечные пределы:

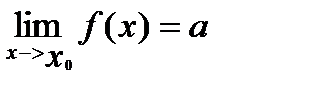
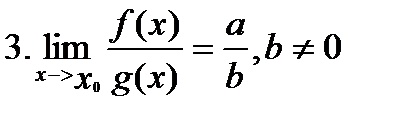
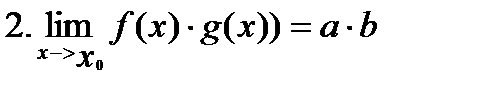
которые соответственно называются теоремами о пределе суммы, произведения, частного.

Рассмотрим основные примеры вычисления пределов.

Пример1. Вычислить предел

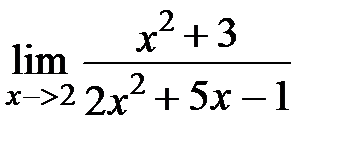
Решение.

Вычислим пределы числителя и знаменателя:

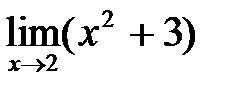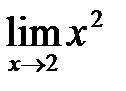= + =4+3=7

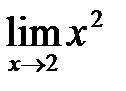=2 +5 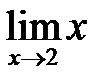-1=8+10-1=17.

Оба предела конечны и предел знаменателя отличен от 0, поэтому применимо утверждение о пределе частного(3):

Непосредственное применение утверждений 1.2.3. в некоторых случаях

не приводит к цели. Мы рассмотрели такие случаи, при нахождении пределов последовательностей и обозначили их неопределенностями видов . Для того, чтобы вычислить (или другими словами “раскрыть”) эти неопределенности необходимо применять тождественные преобразования.

Пример 2. Найти предел.

Решение. Т.к.

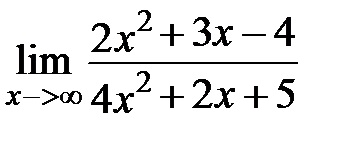
то мы получаем неопределенность вида . Раскрывается она следующим образом:

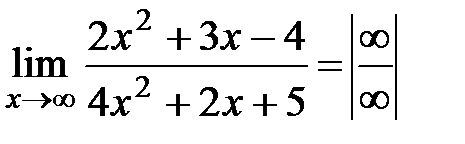
разделим числитель и знаменатель дроби на x²

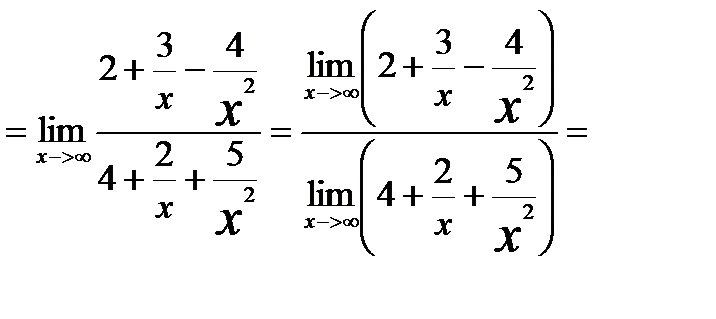
(пределы числителя и знаменателя ¹¥)

Пример 3. Найти предел

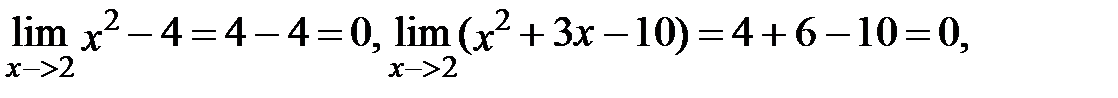
Решение. Т.к.

то исходный предел представляет неопределенность вида 0/0. Для того, чтобы раскрыть ее, необходимо выделить в числителе и знаменателе сомножители, стремящиеся при x®2 к нулю:

= (Далее можно сократить числитель и знаменатель на x-2, т.к. этот сомножитель стремится к нулю при x®2, и можно считать, что он в 0 не обращается) =

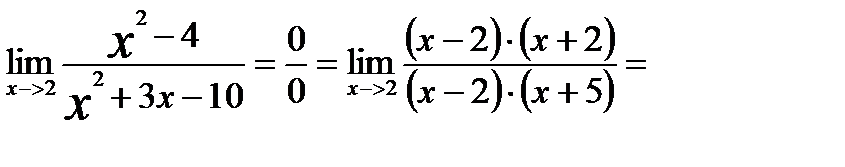
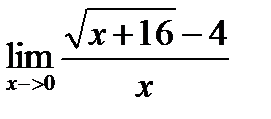
Пример 4. Найти предел

Решение. При подстановке предельного значения x=0 получаем неопределенность вида 0/0. Поэтому домножим числитель и знаменатель дроби на выражение

= (разделим числитель и знаменатель на x, что допустимо, т.к. по определению предела x®0) = .

Дата добавления: 2014-12-23