Слабая компактность шара в сопряженном пространстве. Теорема о вложенных шарах (с док-ом)

Операторы с чисто точечным спектром. Теорема о связи с собственными значениями (с док-ом).

Значения , при которых оператор 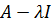обратим, называются регулярными, а те , где 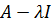необратим, называются нерегулярными.

Множество нерегулярных точек оператора называется спектром оператора.

В n-мерном пространстве понятия собственного значения и нерегулярной точки совпадают. Но в общем случае спектр содержит все собственные значения, но может кроме них содержать ещё кое-что другое.

Резольвентное множество - множество точек оператора, где 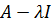обратим. При этом 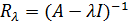называется резольвентой оператора

Совокупность собственнх значений оператора называется точечным спектром оператора. Остальная часть спектра называется непрерывной.

M - метрическое пространство.

Теорема (О вложенных шарах). Пусть пространство M полно, и 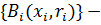последовательность вложенных замкнутых шаров, причем 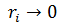. Тогда их перечесление не пусто.

Поскольку 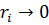, а 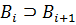, последовательность будет фундаментальной и потому сходится к некоторому x ∈ M в силу полноты пространства. Покажем, что x является искомой точкой. Действительно, если бы нашёлся шар Bi0 такой, что 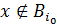, тогда бы точка x не лежала бы ни в одном из шаров, начиная с

номера 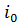. Но поскольку дополнение к 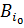открыто, x можно отделить окрестностью от всех шаров, начиная с номера 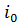. Это противоречит тому, что x-предел последовательности центров шаров.

Замечание. Очевидно, что в силу сходимости 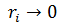это пересечение будет состоять из одной точки. Действительно, если бы их было две, то расстояние d между ними было бы ненулевое. Когда радиусы шаров станут меньше, чем , эти две точки не поместятся в шаре такого радиуса одновременно.

Теорема (О слабой компактности). Пусть X - сепарабельное нормированное пространство. Тогда всякое ограниченное бесконечное подмножество в 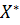является слабо предкомпактным.

Выберем в X счётное всюду плотное множество Пусть 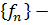ограниченная последовательность функционалов. Рассмотрим последовательность чисел 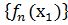. Она ограничена, а потому содержит сходящуюся. Обозначим её через 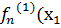). Рассмотрим последовательность чисел 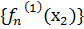. Она тоже содержит сходящуюся подпоследовательность 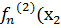). Продолжая этот процесс и выделяя диагональ 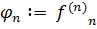, получаем последовательность функционалов, которая сходится на всех векторах

Покажем, что сходимость имеет место для всех векторов x ∈ X. Покажем фундаментальность последовательности 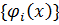. Рассмотрим последовательность элементов из D, сходящуюся к x, тогда, очевидно,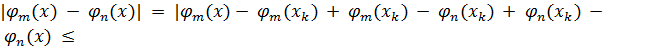

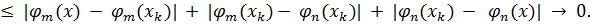
Теорема доказана.

Дата добавления: 2015-04-24