Метод ітерацій та Зейделя

Застосування методу Гаусса для розв’язання системи лінійний рівнянь з великою кількістю невідомих досить громістке. В цих випадках краще використовувати ітераційні методи, тобто методи, які дозволяють будувати послідовність наближень, границя якої буде розв’язком системи лінійних рівнянь. Безумовно, що ця система повинна мати один, єдиний розв’язок.

Спочатку потрібно систему лінійних рівнянь подати у вигляді:

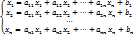(1)

Якщо виконується хоча б одна із умов 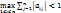, , , 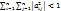то система рівнянь (1) має єдиний розв’язок, який є границею послідовності, що одержується методом простої ітерації або методом Зейделя.

Зауважимо, що систему n лінійних рівнянь з n невідомими, записану в традиційній звичній для нас формі, завжди можна подати у вигляді (1), причому так, щоб виконувалися умови збіжності. Наприклад, якщо модуль кожного діагонального елемента матриці системи більший від суми модулів інших елементів рядка, тобто

, i =1,2,…, n (2)

то, розв’язавши перше рівняння відносно х ₁, друге – відносно х ₂ і т.д., дістанемо систему:

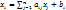, (i =1, 2,..., n), де , 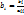. При цьому буде виконуватися перша умова збіжності. Якщо ж система така, що умова (2) не виконується, то за допомогою елементарних перетворень системи можна домогтися її виконання.

Для розв’язання системи рівнянь методом простої ітерації за початкове наближення можна брати довільні значення коренів, наприклад, підставляти значення вільних членів (х1 = b ₁, х ₂= b ₂,..., х_n = b_n). Підставляючи їх в праві частини системи (1), ми одержимо нові значення невідомих. Знову підставляємо одержані корені в праві частини системи (1), одержуючи нові значення невідомих і т.д. Цей процес продовжують до тих пір, поки не досягнуть бажаної точності.

Метод Зейделя відрізняється від методу простої ітерації тільки тим, що при обчисленні х_і на k -му кроці враховуються значення х ₁, х ₂,..., х_{k –1}, обчислені не на попередньому а на цьому самому кроці. Завдяки тому, що значення цих коренів одержуються в якійсь мірі уточненими, метод Зейделя має кращу збіжність в порівнянні з методом простої ітерації.

Дата добавления: 2015-05-23