Властивості функцій неперервних на компакті

Коли ми вивчали функції дійсної змінної, то ми бачили, що якщо функція неперервна на сегменті, то вона мала цілий ряд властивостей. Деякі з цих властивостей мають місце для функцій неперервних на компактах.

Нехай маємо метричні простори Х і У, через 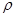будемо позначити відстань в Х, 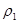– відстань в У; КÌ Х компакт в Х.

Теорема 4.1. Якщо функція f неперервна на компакті К, то образ f(К), цього компакта, є компактом.

Доведення. Нехай f:KÌ X®Y неперервна функція на компакті К. Через f(К) позначимо образ К при даному відрбраженні. Покажемо, що f(К) компакт. Нехай у₁, у₂,..., у_п... послідовність з f(К). Через х_п позначимо 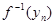– прообраз у_п. Якщо якась точка у_п має декілька прообразів, то будемо брати будь-який з них. Таким чином ми отримали послідовність { х_п }, х_п є К. Так як К компакт, то з { х_п } можна виділити підпослідовність 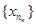, яка збігається до точки, яка належить К. Нехай 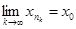, f(х₀)=у₀ Î f(K). Розглянемо підпослідовність 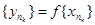послідовності { у_п }. Поскільки f неперервна в х₀, то 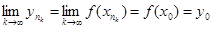. Звідси й слідує, що К є компактом.

Нехай ЕÌ Х, f:Е®У. f(Е), образ Е при даному відображенні. Якщо виявиться, що для кожного у є f(Е) існує тільки одне х є Е таке, що f(х)=у, то на f(Е) можна визначити функцію, яка кожному уÎf(Е) ставить у відповідність хÎЕ таке, що f(x)=y. Ця функція називається оберненою до f. Позначають обернену функцію: 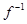. Зрозуміло, що областю визначення оберненої функції є f(E),а областю значень – Е. При цьому f є оберненою до .

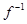Очевидно, для того, щоб функція f мала обернену, тобто була оборотною, необхідно і достатньо, щоб відображення f:E®f(E) – було взаємно-однозначним.

Теорема 4.2. Якщо функція f:KÌX®Y, неперервна на компакті і відображення f:K®f(K) – взаємно-однозначне, то обернене відображення 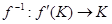-неперервне на f(K).

Доведення. Доведення проведемо методом від супротивного. Припустимо, що 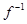не є неперервною функцією на f(K). Тоді існує y₀Îf(K) таке, що в ній 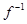має розрив. Нехай f ^{- 1} (y₀)=х₀. Оскільки f ^{- 1} має розрив в точці у₀, то існує e >0 таке, що для кожного натурального п, знайдеться у_пÎf(K) таке, що 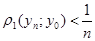,але 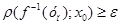. Нехай х_п=f ^{- 1} (у_п), х_пÎК. Так, як К компакт, то з послідовності { x_n } можна виділити підпослідовність 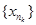, яка збігається до точки із множини К, 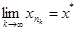, з нерівності 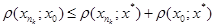слідує

,

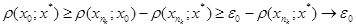коли 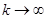. Звідси робимо висновок, що х₀¹х^*. Внаслідок неперервності f маємо

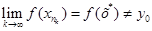(4.1)

(f (x^*)¹ y₀, так як у₀=f(x₀), а відображення взаємно-однозначне). З іншого боку 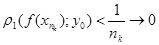, коли 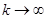, тобто 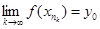, що суперечить (4.1). Теорему доведено.

Теорема 4.3. Якщо функція f:KÌX®Y, неперервна на компакті К, то вона і рівномірно неперервна на К.

Доведення. Доведення проведемо методом від супротивного. Припустимо, що функція f не є рівномірно неперервною на К. Тоді існує e₀ >0 таке, що для кожного натурального п знайдуться точки 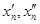, які належать множині К такі, що 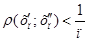, але .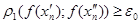

Одержали дві послідовності 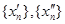. Поскільки К – компакт, то з можна виділити підпослідовність 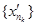, яка збігається до точки х₀, яка належить К. Розглянемо підпослідовність 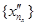послідовності 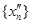. З нерівності 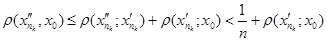слідує, що 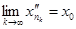. Так, як функція f неперервна в точці х₀, то 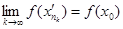і 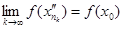. Тобто

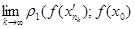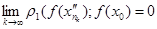= (4.3).

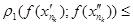
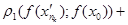
З нерівності 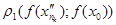робимо висновок, що 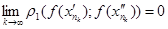, що суперечить нерівності 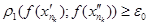при всіх натуральних k. Теорему доведено.

Розглянемо деякі властивості функцій неперервних на компакті, значення яких є дійсні числа, тобто f:KÌX®R (R – множина дійсних чисел). Такі функції називаються числовими.

Теорема 4.4. (Вейєрштрасса) Якщо числова функція неперервна на компакті КÌХ, то вона обмежена на К і приймає на ньому найбільше та найменше значення.

Доведення. Нехай f:KÌX®R є неперервною на К. Внаслідок Т.4.1, множина f(K) –компакт, а, оскільки, компакт є обмеженою множиною, то f(K) є обмеженою множиною.

Доведемо, що функція приймає найбільше і найменше значення на К, тобто існують точки х ₁і х ₂ такі, що для всіх хÎК виконується нерівність: 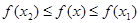. Нехай 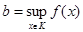. Візьмемо e >0. Тоді існує хÎК таке, що 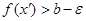. Звідси робимо висновок, що b є точкою дотику f(K). Внаслідок замкненості f(K) (Т. 1.1), bÎf(K). Значить існує х₁ÎК, що f(x₁)=b.

Аналогічно показуємо, що існує х₂ÎК таке, що f(x₂)=а, де 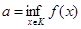. Теорема доведена.

Дата добавления: 2015-05-24