Лабораторная работа №6. Оптимальное созревание сырокопченой колбасы (динамическое программирование)

Уравнение (11), называемое уравнением Беллмана, представляет собой рекуррентное соотношение, позволяющее последовательно определять оптимальное управление на каждом шаге управляемого процесса.

Оптимальным называ­ется такое управление из множества допустимых уп­равлений U, при котором для объекта, описываемого дифференциальным уравнением (1), и заданных огра­ничениях на используемые ресурсы (3) критерий ка­чества управления (2) принимает минимальное (мак­симальное) значение.

Сформулированная подобным образом задача опти­мального управления относится к классу вариационных задач, решением которых занимается раздел математи­ки, получивший название вариационного исчисления.

Величина J₁(u), определяемая соотношением (2), по­лучила название функционала.

В отличие от функции, например f{x), численные значения которой задаются на множестве значений аргумента х, численные значе­ния функционала J₁(u) задаются на множестве всевоз­можных управлений u(t).

Задача нахождения оптималь­ного управления сводится к тому, чтобы из множества допустимых управлений U выбрать такое, при кото­ром функционал J₁(u) принимает минимальное числен­ное значение.

При отыскании оптимального управления вариационными методами приходится сталкиваться с трудностя­ми, ряд которых носит принципиальный характер:

1. Вариационные методы дают возможность находить только относительные максимумы и минимумы функционала J(u), тогда как интерес представляет нахождение абсолютного максимума или минимума.

2. На значения управляющих сигналов обычно бывают наложены ограничения, делающие невозможным поиск оптимального управления вариационными методами.

Трудности, состоящие на пути решения задачи оптимизации управления, привели к интенсивному изучению проблемы оптимальности рядом ученых в Советском Союзе и в США. Советские математики Л. С. Понтрягин и его ученики В. Г., Болтянский, Р. В. Гамкрелидзе, Е. Ф. Мищенко создали теорию оптимального управления, в основе которой лежит сформулированный Л. С. Понтрягиным принцип максимума. Этот принцип позволил поставить теорию оптимального управления на строгую математическую основу и открыл широкие возможности для ее практического применения в обла­сти автоматических систем управления.

Американский математик Р.Беллман разработал иной подход к вычислению оптимальных процессов, получивший название динамического программирования. Метод динамического программирования дает в руки специалиста эффективную вычислительную процедуру решения задач оптимизации управления, хорошо приспособленную к использованию ЭВМ. Для дискретных систем (а на ЭВМ все системы можно рассматривать как дискретные) математическая формулировка метода динамического программирования сводится к следующему.

Имеется объект управления, состояние которого характеризуется многомерной дискретной пере­менной.

(4)

Характер процессов в объекте управления можно изменять, используя то или иное уп­равление из пространства допустимых управлений U. В общем случае управление uÎU может быть также мно­гомерной величиной. Выбор управления u_k производится только в дискретные моменты, k=0,I,., n-1.

Характер движения объекта управления описывает­ся системой разностных уравнений

(5)

За критерий оптимальности принимается сумма вида

(6)

где Q (x_k, u_k) – потери на шаге k, зависящие от состояния объекта x_k и управления на данном шаге u_k. Оптимальным называется такое управление u из множества допустимых управлений U, при котором для объекта, описываемого разностным уравнением (4), критерий оптимальности(6) принимает минимальное (максимальное) значение. Теперь задача заключается в выборе таких управлений u₀,u₁,...u_n-1, которые обеспечивают минимальное значение суммы (6).

Это минимальное значение критерия n-шагового процесса будет зависеть только от начального состояния х₀ и его можно обозначать f_n(x₀). По определению имеем:

(7)

Заметим, что первое слагаемое этого выражения Q(x₀,u₀) зависит только от управления u₀, тогда как остальные слагаемые зависят как от u₀, так и от управлений на других шагах. Так, Q(x₁,u₁) зависит от u₁, но оно зависит и от u₀, так как x₁=T(x₀,U₀).

Аналогично обсто­ит дело и с остальными слагаемыми. Поэтому выраже­ние (7) можно записать в виде

(8)

Заметим далее, что выражение

представляет собой минимальное значение критерия качества управления (n–1) -шагового процесса, имеющего начальное состояние x₁. Эту величину можем обозначить через f_n-1(x₁)

Таким образом, получаем:

(9)

Эти рассуждения можно повторить, если рассмотреть (n-1)-шаговый процесс, начинающийся с начального состояния x₁. Продолжая рассуждения, получаем аналогичное выражение для (n-1) шагового процесса, начинающегося с состояния х_l.

(10)

Сама идея оптимизации управления на каждом шаге отдельно, если трудно оптимизировать сразу весь процесс в целом, не является оригинальной и широко используется на практике. Однако при этом часто не принимают во внимание, что оптимизация каждого шага еще не означает оптимизацию всего процесса в целом. Особенностью метода динамического программирования является то, что оно совмещает простоту решения задачи оптимизации управления на отдельном шаге с дальновидностью, заключающейся в учете самых отдаленных последствий этого шага.

Из основного свойства оптимального управления следует, что оптимизация управления для произвольной стадии многошагового процесса заключается в выборе только последующих управлений.

Поэтому бывает удобным учитывать не те шаги, которые уже были пройдены, а те, которые осталось проделать, для того, чтобы привести процесс в конечное состояние. С этой точки зрения уравнение (10) удобно записать в иной форме. В выражении (10) величина n-1 означает число шагов до тконца процесса. Обозначим эту величину через k. при этом величины x_i и u_i будем обозначать просто через x и u. Они будут означать состояние объекта и примененное управление за к шагов до конца процесса. Последующее состояние, т.е. то, к которому объект переходит из состояния х при применении управления u, обозначим через х`. При этом соотношение (10) примет вид

(11)

0,3

0,2

0,1

1,3

1,2

1,1

2,3

2,2

3,1

3,0

0,0

1,0

2,1

2,0

7 4

2 4

5 4

2 4

2 4

1 4

3,3O

Рис. 1.

3,22P

B

Пример задачи динамического программирования. Динамическую систему необходимо перевести из точки А в точку В (см.рис.1). Движение возможно только по горизонтали справа налево (управление) или по вертикали снизу вверх (управление u₂). На рисунке задана цена перехода из одного узла в другой. Нужно выбрать такой путь, чтобы суммарная цена была минимальной. Внутри окружностей заданы координаты каждого узла.Как бы мы ни двигались, решение задачи требует шести шагов. Будем решать задачу «наоборот», двигаясь из точки В с координатами (0,0) в точку А с координатами (3,3). В этом случае возможно движение только вниз или справа налево.

Рекуррентная формула для решения задачи методом динамического программирования имеет вид:

Будем действовать в соответствии с этой формулой (рис.1). Рассмотрим переход в каждую точку нашей системы и, если возможны варианты переходов, выберем тот переход, для которого общая сумма потерь является наименьшей. Начинаем движение из точки (0,0). В этой точке еще никаких потерь нет, поэтому ставим в прямоугольник около 2222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222узла число 0. В т.(1,0) можно перейти только из т.(0,0) с платой 4 единицы. Рисуем стрелку и ставим около узла число 4. В т. (2,0) можно перейти только из т.(1,0) с общими потерями 4+1=5. Рисуем стрелку и ставим это число около узла. Аналогично проводим стрелки и заполняем узлы (3,0), (0,1),(0,2) и (0,3). После этого рассмотрим переход в т. (1,1). В нее можно перейти из т. (1,0), при общих потерях 4+8 =12, и из т. (0,1) с общими потерями 8+7 =15. Выбираем первый путь, проводим стрелку и ставим около узла число 12. В т. (1,2) можно перейти из т. (0,2) или из т.((1,1). Выбираем второй путь, так как при нем общие потери 12+7=19 меньше. Аналогичным образом просчитываем и выбираем переходы ко всем остальным точкам. В результате оказывается, что существует только один путь к т. (3,3). Он то и является оптимальным. На рис.1 он выделен жирными стрелками.

До построения собственно программы задаем координаты начальной и конечной точек, объявляем о начале отсчета с 1 (ORIGIN:=1), задаем значения коэффициентов a,b и выбираем шаг d (см. рис. 2).

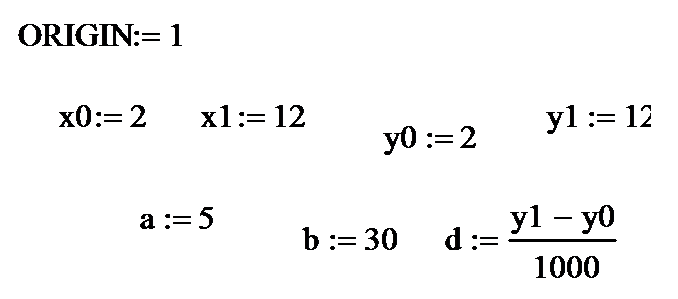
Рис.2

Сама программа приведена на рис.3.

В доцикловой части программы задаем начальные значения переменным x,y и функции S.

В начале цикла в операторе for определяем количество точек. Мы проведем вычисления для четырех точек. Соответственно, j=0..3 Очевидно, что каким путем мы бы не шли, нам придется пройти (x1-x0)/d точек по горизонтали и (y1-y0)/d точек по вертикали, т. е. всего [(x1-x0)+(y1-y0)]/d точек.

Далее в цикловой точке мы, прежде всего, выбираем управление, минимизируя полную цену. Полная цена всего движения для данного участка состоит из цены движения на всех предыдущих этапах S и приращения цены при движении на данном участке. При движении по горизонтали это приращение равно ax ², при движении по вертикали – by.

Рис.3. Программа выбора оптимальной траектории

Но так как движение системы не должно выходить за пределы квадрата x1-x0, y1-y0, то одновременно при выборе управления мы проверяем нахождение системы в этом квадрате. Для возможности движения по вертикали должно выполняться условие

y ≤ y1, а для возможности движения по горизонтали – условие x ≤ x1. Выбрав управление, мы подсчитываем новое значение полной цены S и определяем новые значения координат x и y.

Для сохранения в памяти и вывода на печать вводим новые значения в столбцы матрицы V. Программа составлена.

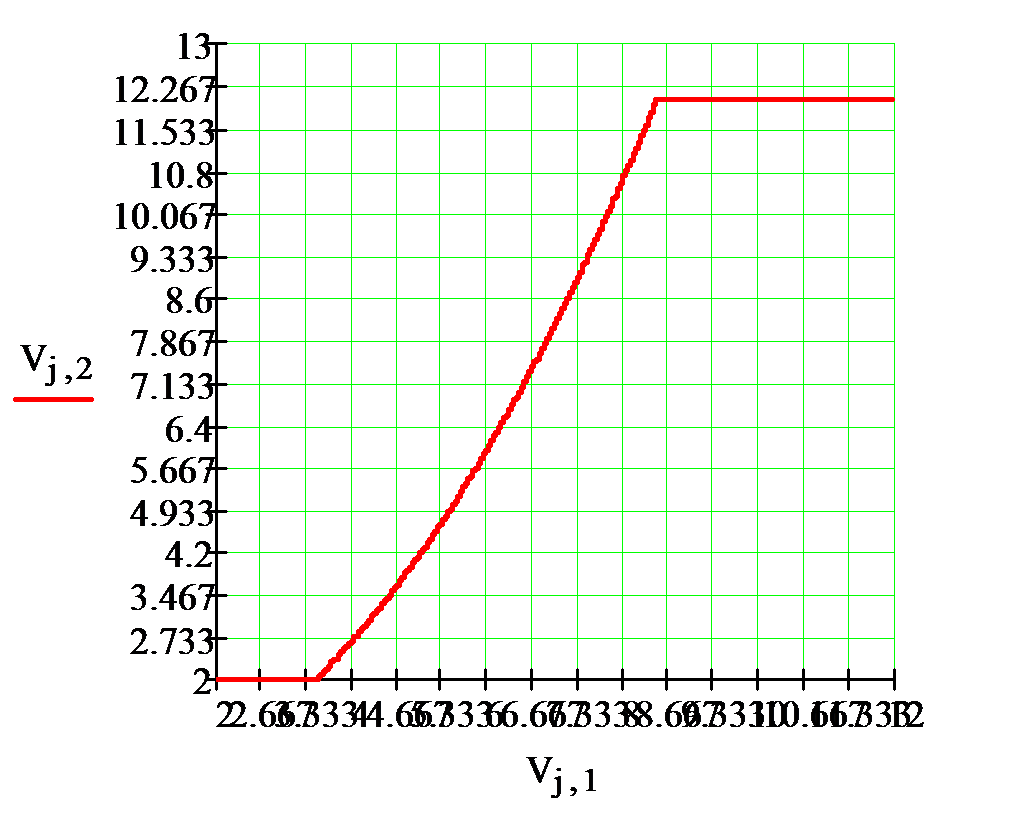
На рис.4 представлен график решения задачи.

Рис.4. График оптимальной траектории.

Рассмотрим задачу оптимального управления созреванием сырокопченых колбас.

Процесс производства сырокопченых колбас состоит в составлении фарша из исходного сырья (говядины высшего сорта, полужирной свинины, шпика), который затем шприцуется в оболочку, и полученные батоны колбасы помещаются в камеру созревания.

. В процессе созревания происходят распад белков, накопление ароматобразующих веществ и другие биохимические реакции. Все эти превращения приводят к накоплению молочной кислоты в колбасе, что ведет к изменению показателя его кислотности рН.

С целью сокращения созревания сырокопченых колбас в них при составлении фарша вносятся стартовые культуры. Стартовые культуры способствуют подавлению жизнедеятельности патогенной микрофлоры за счет деятельности молочнокислых бактерий.

Управлять процессом созревания сырокопченых колбас можно, варьируя управляющие величины: количество и состав стартовых культур, температуру t ◦ С и влажность воздуха ψ % в камере созревания. Эти же величины являются и контрольными, так как их можно наблюдать. Управляемой величиной является показатель кислотности pH.

Результаты экспериментальных исследований показали, что процесс созревания занимает 21 день и его можно расчленить на восемь шагов, в результате каждого из которых достигается определенные значения показателя кислотности полуфабриката.

1-ый шаг — начальный этап (составление фарша) и первый день созревания, рН₁ =(5,60+5,80);

2-ой шаг — второй день созревания, pН₂ = (5,50 +5,70);

3-ий шаг — третий день созревания, рН₃ = (5,35 +5,5);

4-ый шаг—четвертый день созревания, рН₄ = (5,20 +5,40);

5-ый шаг — пятый день созревания, рН₅ =(5,10 +5,30);

6-ой шаг — шестой день созревания, рH ₆ =(4,90+5,10);

7-ой шаг—с седьмого по двенадцатый день созревания, рН₇ =(4,80+5,00);

8-ой шаг—с девятого/двенадцатого по двадцать первый день созревания, рН₈ =(5,30).См таблицу 1.

Здесь t и ψ – практически используемые значения управляющих величин, pH – получаемые при таком управлении значения показателя кислотности, pHmin и pHmax – мини

микрофлоры стартовых культур. В результате ша­гов 2-6 происходит подавление жизнедеятельности патогенной микро­флоры, накопление молочной кислоты, что обусловливает сдвиг рН в «кислую» сторону. По существу на первом – шестом шагах выбираются допустимые управления, обуславливающие качество готовой продукции. Седьмой шаг приводит значение pH к минимуму. Восьмой шаг поддерживает термовлажностные параметры, необходимые для получения продукта заданного качества с конечным результирующим значением pH=5,3. На последних двух шагах управление не варьируется.

Таблица 1

День
pH	5.6	5.55	5.5	5.4	5.3	5.2	5.1	5.0	4.9	4.85	4.8	4.8	4.8
PHmin	5.6	5.6	5.5	5.35	5.2	5.1	4.9	4.8	4.8	4.8	4.8	4.8	4.8
pHmax	5.8	5.8	5.7	5.5	5.4	5.3	5.1	5.0	5.0	5.0	5.0	5.0	5.0
t
ψ
шаги

Продолжение таблицы 1

4.85	4.9	4.95	5.0	5.1	5.2	5.25	5.3	5.3
5.3	5.3	5.3	5.3	5.3	5.3	5.3	5.3	5.3
5.3	5.3	5.3	5.3	5.3	5.3	5.3	5.3	5.3

В качестве математической модели процесса созревания сырокопченой колбасы выберем авторегрессионую зависимость,

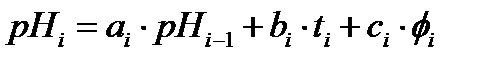
(1)

Анализ таблицы 1 показывает, что коэффициенты «b» и «c» практически постоянны, поэтому примем b=-6*10^-4, а c=0,95*10^-4. Коэффициент «a» несколько более изменяется в процессе созревания колбасы, поэтому для этого коэффициента были приняты зависящие от номера шага Значения, приведенные в таблице 2.

Таблица 2.

Шаг
день
«а»		0.99	0.98	0.98	0.98	0.98	0.99	0.99	0.99	0.99	0.99

1.01	1.01	1.01	1.01	1.02	1.02	1.01	1.01

Продолжение таблицы 2

Созданную математическую модель необходимо, прежде всего, исследовать на адекватность. Для этого вычисленный по ней показатель кислотности сравнивался с показателем из таблицы 1 при значениях управляющих величин из этой же таблицы. Для этого была создана программа в Маткаде, приведенная на рис.1.

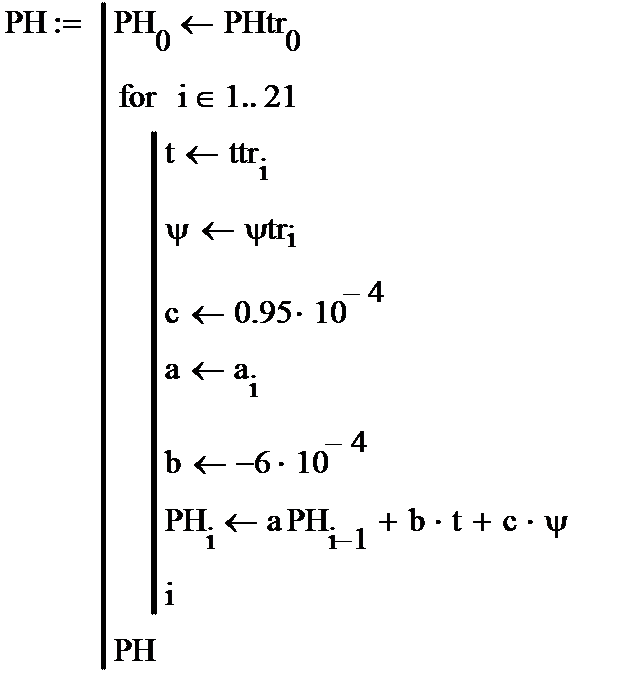
Рис.1. Программа проверки адекватности системы экспериментальным данным и ошибка модели в %

Результаты расчетов по программе приведены в таблице 3.

Таблица 3

Шаг
День
pH практ	5.6	5.55	5.5	5.4	5.3	5.2	5.1	5.0	4.9	4.85	4.8	4.8	4.8
pH мат	5.6	5.484	5.371	5.313	5.20	5.09	4.99	4.89	4.79	4.74	4.69	4.69	4.69
Ошибка %		0.174	1.35	1.61	1.8	1.9	1.0	0.12	0.87	0.87	0.84	0.81	0.74

Продолжение таблицы 3

4.74	4.78	4.83	4.87	4.97	5.08	5.12	5.17	5.3
4.837	4.884	4.931	4.979	5.077	5.177	5.228	5.279	5.277
0.74	0.68	0.63	0.59	0.57	0.58	0.59	0.61	0.7

Из таблицы 3 видно, что относительная ошибка не превышает 2%. Таким образом, созданная математическая модель хорошо отображает экспериментальные данные.

Мы хотим так изменить управление процессом созревания сырокопченой колбасы, чтобы хотя бы немного улучшить ее качество. Так как по мере созревания кислотность полуфабриката должна снижаться, то для улучшения качества необходимо уменьшать кислотность. Для оценки качества управления процессом будем использовать функциональный критерий - выигрыш J в виде относительного суммарного количества патогенной микрофлоры, прекратившей свою жизнедеятелъностъ в результате накопления массы молочнокислой микрофлоры, а также количества расщепленных белков и других эссенциальных веществ.

Запишем основное рекуррентное уравнение динамического программирования, используя в качестве функции выигрыша

(2)

что обусловлено фактом снижения значения рН при увеличении значения J. Так как на восьмом шаге происходит лишь поддержание параметров, то оптимизацию необходимо проводить только для первых семи шагов.

Из выбранной функции выигрыша следует, что условную оптимизацию всех шагов возможно проводить, выбирая такие управления, при которых.

Как было сказано выше, управлением является количество и состав стартовых культур, а также температура и влажность в камере созревания. В качестве множества допустимых управлений технологией было выбрано множество Ωу = {18°С + 25°С} х {80% + 90%}, образованное путем комбинаций (прямого произведения) возможных значений температур и относительной влажности воздуха в камере созревания. Безусловная оптимизация управления соответствует таким наборам {t _k, ψ_k} управляющих воздействий, при которых оптимальная кривая рН _opt проходит ниже всех используемых на практике технологий, т.е. площадь под кривой рН будет минимальной.

Была составлена программа в Маткаде, которая приведена на рис.6.После ввода начальных значений температуры, влажности, показателя кислотности и критерия оптимальности начинается варьирование управляющих параметров.

В программе управление температурой t и влажностью f ведется на первых шести шагах

(i= 1…6).

На каждом из этих шагов выбираются путем перебора значения t и f, минимизирующее критерий оптимальности J – сумму значений показателя кислотности на всех предыдущих шагах.

Для этого сформированы два вложенных цикла по температуре (t1) и влажности (f1), соответственно. Начиная с седьмого дня значения температуры и влажности задаются постоянными (t=15 град. C, f=80%).

В результате расчетов получены необходимые для оптимального решения значения управляющих параметров, значения критерия оптимальности в случае оптимального и не оптимального решений, графики и таблицы значений показателя кислотности для обоих случаев (см. рис.7).

На этом рисунке в части А приведены оптимальные значения управляющих параметров – температуры и влажности. В части Б рисунка приведены значения критерия оптимальности для случаев оптимального

Jopt =101.755 и традиционного Jtr=107.35 управлений, а также изменение этого критерия в результате оптимального решения

DJ= 5.21%

. В части В показаны значения показателя кислотности при оптимальном управлении, а в части Г по шагам графики показателя кислотности при оптимальном (крестики) и традиционном (кружочки) управлении.

Рис.6. Маткад программа определения оптимальных параметров выдержки сырокопченой колбасы методом динамического программирования.

Следует заметить, что во-первых полученное улучшение качества колбасы (величины показателей кислотности) незначительно, что указывает на хороший профессионализм практиков, и во-вторых оптимальное решение крайне чувствительно к значениям коэффициентов используемого разностного уравнения. режима созревания сырокопченой колбасы.

А)

Б)

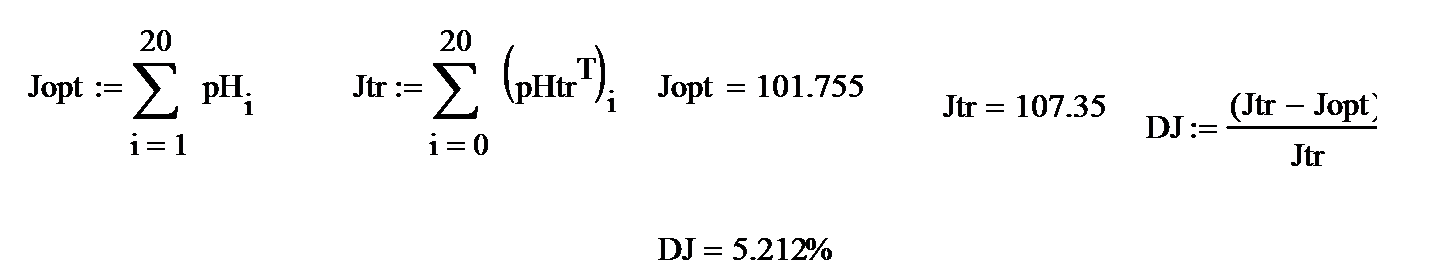
В)

Г)

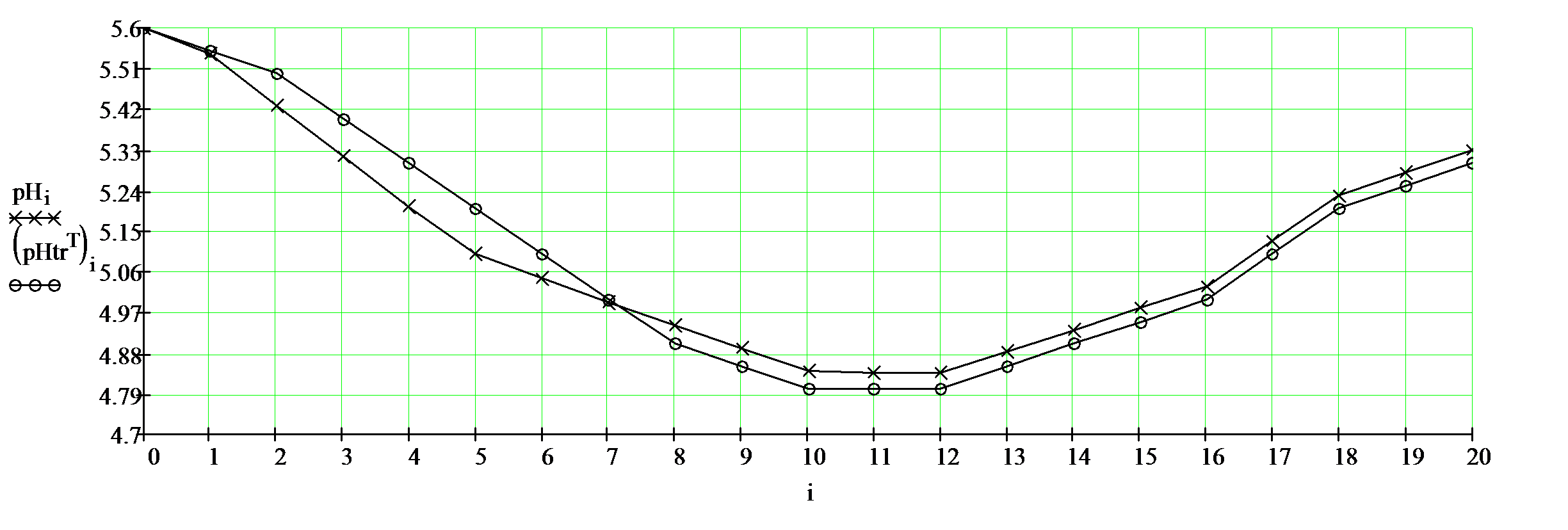
Рис.7. Результаты расчета оптимального режима созревания сырокопченой колбасы.

А)- Необходимые для оптимального процесса значения температуры и влажности по шагам.

Б) Полученная экономия критерия оптимальности DJ= 5,212%.

В) Значения показателя кислотности при оптимальном процессе.

Г) График значений показателя кислотности при оптимальном (крестики) и стандартном (кружочки) процессах.

Дата добавления: 2015-06-27