Стохастическое динамическое программирование)

ЛАБОРАТОРНАЯ РАБОТА № 7. ОПТИМИЗАЦИЯ РАБОТЫ ПРЕДПРИЯТИЯ.

Стохастические задачи. Типичным для задач управления является случай, когда имеющаяся информация бывает или недо­статочна для точной оценки ситуации, или искажена по­сторонними факторами. Тем не менее, недостаточность информации не снимает задачи принятия решения. Осо­бенность задач управления именно в том и состоит, что решение должно быть обязательно принято независимо от того, в состоянии ли мы точно оценить результаты, к которым приведет принятое решение. Таким образом, в процессе управления возникает важная задача принятия решения в условиях, когда ин­формация о сложившейся ситуации или недостаточна, или искажена. Данная задача получила название зада­чи принятия решения в условиях неопределенности.

Метод динамического программирования позволяет решать вероятностные задачи.

Задача 1. Завод выпускает продукцию. Он может находиться в двух состояниях:

1. спрос на продукцию есть;

2. спроса на продукцию нет.

Работой завода можно управлять с помощью двух стратегий:

1. стратегия 1 – не тратиться на рекламу и научные исследования;

2. стратегия 2 – тратиться на них.

Для каждой стратегии задана своя стохастическая матрица (матрица вероятностей перехода из одного состояния в другое и своя матрица доходов.

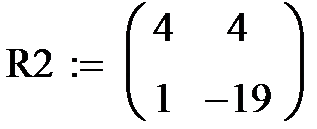
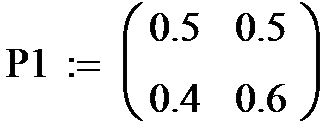
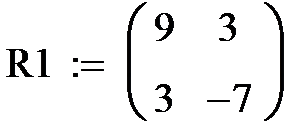
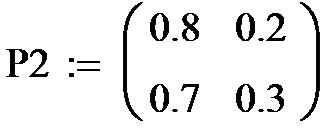
Здесь P1, P2 – матрицы вероятностей переходов завода из одного состояния в другое. Например, P1₁₁ – вероятность того, что завод, находящийся в состоянии 1 останется в этом состоянии, P1₁₂ – вероятность того, что завод, находящийся в состоянии 1 перейдет в состояние 2, P1 ₂₂ – вероятность того, что завод, находящийся в состоянии 2 останется в этом состоянии и P1₂₁ - вероятность того, что завод, находящийся в состоянии 2, перейдет в сосотяние1. Таковы же элементы матрицы P2.

В матрице R1 элемент R1₁₁ – ожидаемый доход от деятельности завода, если он останется в состоянии1, R1₁₂ – ожидаемый доход завода при переходе из состояния 1 в состояние 2, R1₂₂ - ожидаемый доход (убыток,т.к. доход отрицателен) завода, остающегося в состоянии 2, R1₂₁ – ожидаемый доход завода при перходе из состояния 2 в состояние 1. Таков же смысл элементов матрицы R2.

Задача состоит в том, чтобы, в каком бы состоянии завод не находился, выбрать стратегию (управление),приносящую максимальный ожидаемый доход.

Перед нами вероятностная задача: управление (выбор стратегии) изменяет вероятность перехода из одного состояния в другое. Переход происходит дискретно, т.е. это дискретный случайный процесс. При выборе стратегии вероятность перехода из одного состояния в другое зависит только от состояния в настоящий момент времени. Следовательно, этот случайный процесс является Марковским.

Ожидаемый доход – это сумма вероятностей получения того или иного дохода.

Рассмотрим первый шаг управления работой завода – первый выбор стратегии. Обозначим через F ожидаемый доход. Если завод находится в состоянии 1, то он может остаться в этом состоянии или перейти в состояние 2. При этом может быть использована как стратегия 1, так и стратегия 2. В первом случае F₁₁ - ожидаемый доход при состоянии 1 и выборе стратегии 1 составляет: F₁₁ =P1₁₁ R1₁₁ +P1₁₂ R1₁₂. После подстановки чисел получим: F₁₁= 6.

Аналогично, при выборе стратегии 2 ожидаемый доход будет составлять F₁₂= P2₁₁R2₁₁+P2₁₂R2₁₂=4.

Однако завод может находиться в состоянии 2 и для управления также может быть выбрана одна из стратегий. В этом случае

F₂₁=P1₂₂R1₂₂+P1₂₁R1₂₁= -3 при выборе первой стратегии и F₂₂=P2₂₂R2₂₂+P2₂₁R2₂₁= -5 при выборе второй стратегии. Эти расчеты можно сделать выбором на первом шаге управления. Для получения максимального ожидаемого дохода следует выбрать стратегию 1 (не использовать научные исследования и рекламу), в каком бы состоянии завод не находился.

На каждом следующем шаге «n» управления мы должны выбирать управление так, чтобы получить максимальный ожидаемый доход за все «n» шагов. Обозначим максимальный ожидаемый доход за первый шаг при нахождении завода в состоянии 1 через f1, а при нахождении завода в состоянии 2 через f2. Из предыдущих расчетов следует, что f1=6 и f2=-3.

На втором шаге управления ожидаемый доход с учетом максимального ожидаемого дохода на первом шаге составит при нахождении завода в состоянии 1 и выборе стратегии1 F₁₁= P1₂₂(R1₂₂+ f1) + P1₁₂ (R1₁₂+f2) =0,5(9+6) + 0,5 (3-3) =7,5 или

F₁₂=P2₁₁(R2₁₁+f1) +P2₁₂ (R2₁₂+f2)=0,8(4+6) +0,2(4-3) =8,2 при выборе стратегии 2.Очевидно, что при нахождении завода в состоянии 1 следует для получения максимального ожидаемого дохода выбирать стратегию 2, т. к. f1=8,2.

При нахождении завода в состоянии два, проведя аналогичные расчеты получим F₂₁=P1 ₂₂ (R1₂₂+f2) +P1₂₁(R1₂₁+f1) =-2,4 при выборе первой стратегии и F₂₂=P2₂₂(R2₂₂+f2) +P2₂₁(R2₂₁+f1)= -1,7 при выборе второй стратегии. Очевидно, что в обоих случаях для получения максимального ожидаемого дохода нужно выбирать стратегию 2.

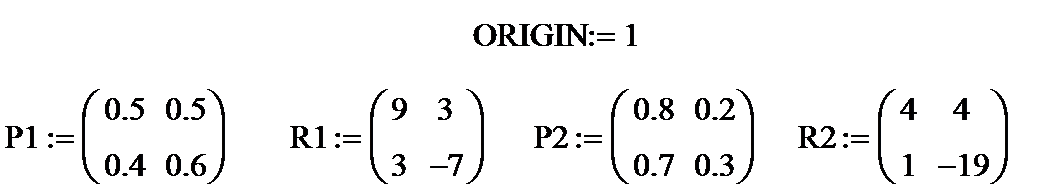Подобным образом рассчитывается оптимальное управление и на всех последующих шагах.

Ниже представлена программа в Маткаде для решения данной задачи.

Запись ORIGIN=1 означает, что счет начинается не с нуля, а с единицы. Далее приводятся матрицы перехода и матрицы доходов для двух стратегий. В самой программе вычисляются доходы F_i,j для всех четырех возможных случаев и выбирается управление «u» в зависимости от того, какие доходы больше. Принято U=1 для первой и U=2 для второй стратегии. После этого формируется вектор «max» для каждого случая. Программа набрана для случая вычисления «u» и приведены его значения для двух шагов управления.

ЗАДАНИЕ: 1. Набрать программу.

2. Вычислить значения векторов «u», «max», двух, пяти и 10 шагов управления.

ЛАБОРАТОРНАЯ РАБОТА №8. ОЦЕНКА КАЧЕСТВА ПИЩЕВЫХ ПРОДУКТОВ.(Оценка качества пищевых продуктов методами регрессионного анализа).

Задача 1. Оценка качества томатов.

В качестве объективного показателя при оценке качества томатов выбрали оптическую плотность при длине волны l=360 нм (m).

Установлена экспериментальная зависимость 10- балльной органолептической оценки (y) от оптической плотности (x):

х	0.98	1.1	1.25	1.39	0.99	1.14	1.28	1.43	1.1	1.22	1.33	1.45
y		4.5	3.5	3.0	5.0	4.5	3.5		4.5		3.5

Для решения задачи объективной оценки качества томатов используем линейную регрессию. В Маткаде, как уже говорилось выше, коэффициенты линейной регрессионной зависимости определяются с помощью встроенных функций slope (наклон) и intercept (отрезок, отсекаемый на координатной оси)

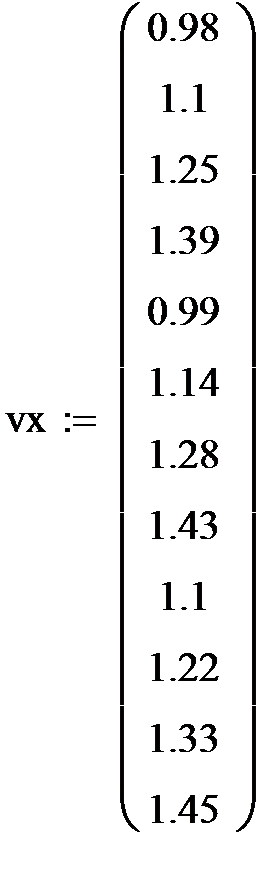
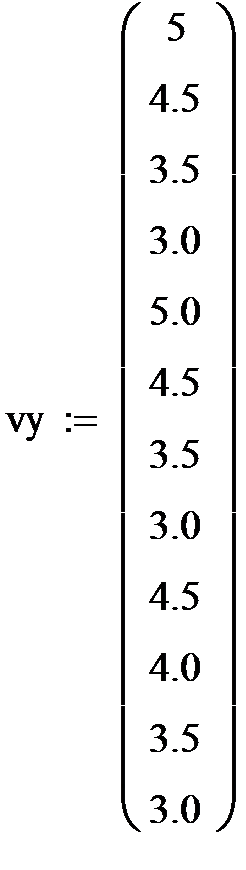
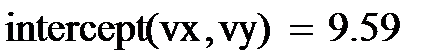
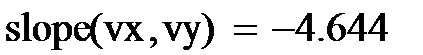
Рис.1. Исходные данные и вычисление коэффициентов регрессии.

На рис. 1 приведены вектора исходных данных – вектор vy- органолептической оценки качества томатов и вектор vx- оптической плотности томатов.

Здесь же показано применение встроенных функций вычисления коэффициентов прямой и уравнение линейной регрессии, использующее эти коэффициенты.

На рис.2 точками показана органолептическая оценка и сплошной линией – аппроксимирующая ее прямая. Здесь же показаны максимальные ошибки оценки в баллах (она равна 0,204 балла) и в процентах (4,083 %).

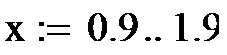
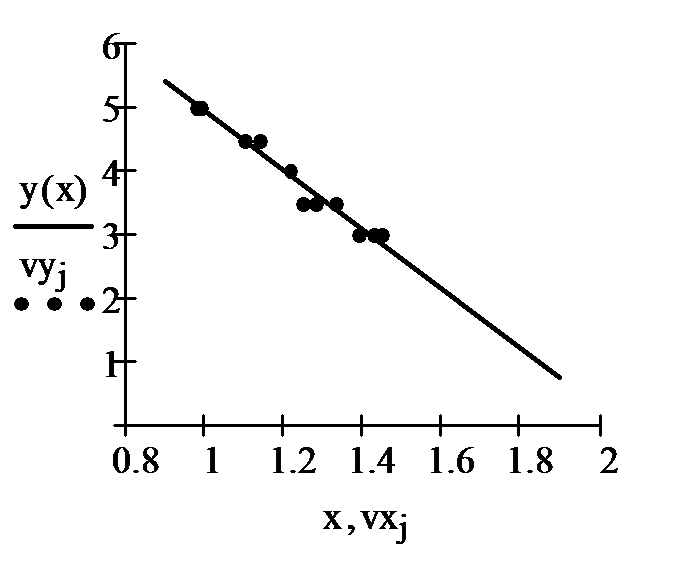
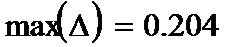
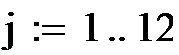
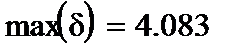
Рис.2 График оценки качества томатов.

Задача 2. Инструментальная оценка качества шампанского

Сегодня существенная часть шампанских вин в России и в мире производится непрерывным способом. Этот способ был разработан в СССР еще в 60-х годах, и авторы разработки Г.Г. Агабальянц, А.А. Мержаниан и С.А. Брусиловский были награждены Ленинской премией. При таком способе производства обычный выборочный органолептический контроль недостаточен. Поэтому задача инструментальной оценки качества шампанских вин является вполне своевременной.

Описанная ниже инструментальная оценка качества шампанского разрабатывалась по статистическим данным, приведенным в (С.П. Авакянц. Биохимические основы технологии шампанского. М., «Пищевая промышленность»1980).

В этой книге приведены экспертные балльные оценки и состав, а также физико-химические, окислительно-восстановительные, биохимические показатели и показатели букетистых веществ (всего 35 показателей) для 59 образцов Советского шампанского.

На основе этих показателей была построена теоретическая балльная оценка, которая сравнивалась с экспертной.

Задача решалась методом наименьших квадратов в пакете Маткад.Решение проводилось в решающем блоке GIVEN с использованием встроенной функции MINERR.

Первоначально была проведена проверка экспериментального материала на выбросы. Оказалось, что весь этот материал статистически достоверен.

Затем были вычислены парные коэффициенты корреляции межу всеми показателями и парные коэффициенты корреляции показателей с органолептической балльной оценкой. В результате для дальнейшего исследования оставлено только следующие восемь показателей с максимальными коэффициентами парной корреляции и максимальными коэффициентами корреляции с балльной оценкой:

Содержание этанола % объема

Титруемая кислотность г/л.

Летучие кислоты г/л,

Содержание ионов железа мг/л,

Устойчивость двусторонних пленок с.,

Оптическая плотность при длине волны λ=280нм.,

Доминирующая длина волны нм.,

Свободные альдегиды мг/л.

На рис.3.показана часть сформированной из этих показателей таблицы М2.

Рис.3. Таблица исходных данных.

Здесь первый столбец – балльная оценка, а остальные столбцы – значения перечисленных выше показателей. Таблица имеет 59 строк и девять столбцов.

Весь отобранный экспериментальный материал был разделен на обучающую и контрольную части.

Обучающая последовательность использовалась для определения параметров аппроксимирующей функции, на контрольной части оценивалась точность оценки качества по этой функции.

Для контрольной части были отведены 10 опытов из 59. Номера экспериментов контрольной части для большей объективности выбирались случайным образом, т. е. они обновлялись при каждом новом решении. Соответственно, рассчитанные параметры и результаты каждого решения несколько отличались один от другого.

На рис.4.показаны операторы и номера строк случайного выбора контрольных экспериментов.

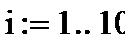
Рис 4. Результат случайного выбора десяти контрольных экспериментов.

С помощью вспомогательной программы контрольные эксперименты были исключены из исходных данных, в результате чего получена показанная на рис.5 таблица М3 опорных значений показателей, по которым и определялась аппроксимирующая гиперплоскость.

Рис.5. Таблица опорных значений показателей

После разделения экспериментального материала на обучающую и контрольную части, на основании значений этих показателей и приведенных экспертных балльных оценок методом наименьших квадратов была построена статистическая функциональная зависимость теоретической балльной оценки от этих показателей. Как известно, выбор вида аппроксимирующей функции в методе наименьших квадратов сам по себе является сложной задачей. В данной работе аппроксимация производилась наиболее простой -линейной функцией вида

(1)

где ball – оценка в баллах, X_j-значение j-ого выбранного показателя; a_j - коэффициенты показателей, значения которых и определяются методом наименьших квадратов.На рис.6. приведено решение задачи в Маткаде в решающем блоке Given.

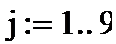
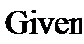
Рис.6. Определение коэффициентов методом наименьших квадратов.

Сначала задаем начальные приближения для искомых коэффициентов a_j. Их всего девять. Затем в блоке given набирается сумма сорока девяти (по количеству строк в таблице М3) квадратов разностей инструментальной оценки (1) и органолептической балльной оценки в первом столбце таблицы М3. Записывается требование равенства нулю этого выражения. Но так как выдержать это требование невозможно, ниже записывается требование определить вектор коэффициентов «а» с минимальной ошибкой (minerr).Задача решается и ниже приведено ее решение – значения элементов матрицы коэффициентов а.

Подобрав коэффициенты «а» мы определили девятимерную линейную функцию, аппроксимирующую зависимость балльной оценки качества шампанского в зависимости от значений объективных показателей. Теперь следует проверить, насколько точно проводится эта аппроксимация.

Сначала проведем эту проверку для опорных значений показателей, а затем для контрольных значений. Результаты проверки относительно опорных значений показателей приведены на рис.7,а результаты проверки относительно контрольных показателей - на рис8.

.

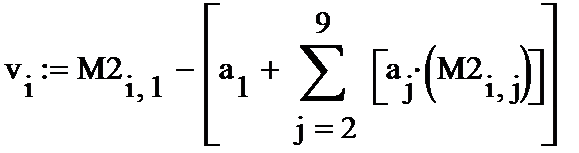
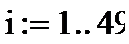
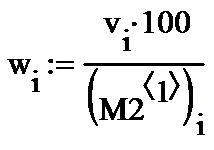
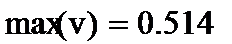
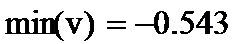
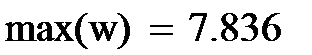
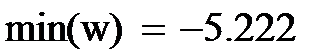
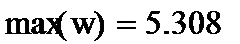
Рис.7.проверка точности аппроксимации для опорных значений показателей.

На рис.7 сначала приведена формула для подсчета абсолютной ошибки v в баллах, где М2- матрица опорных значений показателей, ниже — вектор значений абсолютных ошибок(для экономии места в транспонированном виде), максимальные ошибки в баллах.

Ниже приведена формула для расчета относительной ошибки w в процентах, а также ее максимальное значение. Максимальная ошибка в баллах равна 0,543, а максимальная ошибка в процентах -5,308%.

На рис.8 сначала в транспонированном виде приведен вектор номеров контрольных опытов u, затем приведена формула для расчета инструментальной балльной оценки и формула подсчета абсолютной ошибки W. Ниже приведены значения абслютных ошибок, а также их максимальная и минимальная величины.

Затем на рисунке приводится выражение для относительной ошибки в процентах и максимальное и минимальное значение этих ошибок.

Мы видим, что максимальная ошибка инструментальной балльной оценки контрольных параметров не превышает 0,717 балла, а относительная ошибка не превышает 7,836%.

Проверка показала, что сформированная математическая модель позволяет достаточно точно определять балльность шампанского по измеренным значениям следующих показателей: Содержанию этанола % объема, Титруемой кислотности г/л., Летучим кислотам

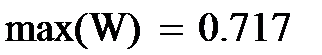г/л, Содержанию ионов железа мг/л, Устойчивости двусторонних пленок с., Оптической плотности при длине волны λ=280нм., Доминирующей длины волны нм., Свободным альдегидам мг/л.

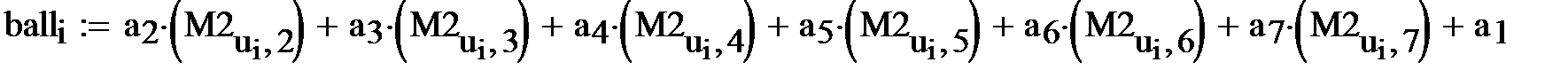
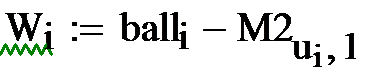
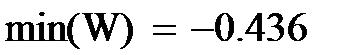
Максимальная и минимальная ошибки в процентах

Рис.8.Проверка точности аппроксимации для контрольных значений показателей.

Дата добавления: 2015-06-27